Einstein'sche Summationskonvention

In der Mathematik kennzeichnet der Index (Plural: Indizes) die Glieder einer Folge oder Reihe oder die Komponenten eines Tupels oder einer Matrix. In den Anfängen der Mathematik der Neuzeit wurde auch ein Funktionswert – f(x) in moderner Schreibweise – mittels tiefgestelltem x als f_x bezeichnet. Die Notation a_i für die Glieder einer Folge (als Funktion über natürlichen Zahlen) kann als Rest dieser älteren Schreibweise angesehen werden.

Wie aus der Schreibung f_x schon hervorgeht, müssen die Indizes keineswegs immer natürliche Zahlen sein. Vielmehr kann jede endliche oder unendliche Menge Λ als Indexmenge benutzt werden, um mathematische Objekte zu einer "Familie" 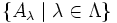$\{A_\lambda \mid \lambda \in \Lambda \}$ zusammenzufassen. (Siehe auch: Mengenlehre, Kartesisches Produkt)

In der Differentialgeometrie werden die Schnitte eines Vektorbündels oft in Indexschreibweise bezeichnet, um die Funktionsschreibweise für algebraische Operationen zwischen Fasern verschiedener Bündel über demselben Punkt frei zu haben.

In der Tensorrechnung, speziell den Tensordarstellungen der Physik, werden doppelte Indizes im Sub- und Superskript zur verkürzten Notation von Summen verwendet (Einsteinsche Summationskonvention).

In den obigen Anwendungen tritt der Index stets als tiefergestellter oder hochgestellter Wert auf. Daneben gibt es noch andere mathematische Bedeutungen des Begriffs "Index":

• Die Anzahl der Äquivalenzklassen einer Äquivalenzrelation, siehe Index (Äquivalenzrelation).
• Als Spezialfall davon: Die Anzahl der linken (oder auch rechten) Nebenklassen einer Untergruppe, siehe Index (Gruppentheorie).
• In der Differentialtopologie als Poincaré-Index zur Klassifikation kritischer Punkte.