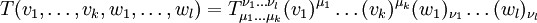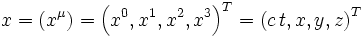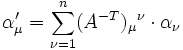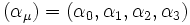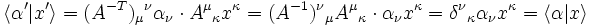Tensordarstellungen der Physik

Die Indexnotation ist eine Form Tensoren schriftlich darzustellen, die vor allem in der Physik und gelegentlich auch im mathematischen Teilgebiet der Differentialgeometrie Anwendung findet.

Am üblichsten ist diese Notation im Kontext der allgemeinen Relativitätstheorie, deren Formulierung in Form von Tensoren erfolgt. Auch einige moderne Texte über spezielle Relativitätstheorie verwenden diese Notation und im Kontext von Eichtheorien ist sie auch in der Quantenfeldtheorie anzutreffen. Diese Notation eignet sich besonders für Rechnungen in lokalen Koordinaten, weshalb sie in der Physik deutlich verbreiteter ist, als in der Mathematik. Die Notation impliziert jedoch keine Koordinatenabhängigkeit, sondern ist auch ohne explizites Koordinatensystem sinnvoll.

Tensoren

In der Differentialgeometrie wird die Geometrie gekrümmter Räume untersucht, die durch sogenannte differenzierbaren Mannigfaltigkeiten beschrieben werden. Diese Mannigfaltigkeiten erlauben an jedem Punkt p die Definition eines d-dimensionalen reellen Vektorraums, der als Tangentialraum in diesem Punkt bezeichnet wird. Wenn die Mannigfaltigkeit in einen höherdimensionalen Raum eingebettet wird, entspricht der Tangentialraum genau der d-dimensionalen Hyperfläche, die die Mannigfaltigkeit im Punkt p berührt und dort zu ihr tangential ist. Der Dualraum des Tangentialraums wird als Kotangentialraum bezeichnet.

Die Elemente eines Tensorproduktes aus k Kopien des Kotangentialraums und l Kopien des Tangentialraums werden als (k,l)-Tensoren bezeichnet. Sie sind also multilineare Abbildungen, die k Elemente des Tangentialraums und l Elemente des Kotangentialraums auf eine reelle Zahl abbilden. Ein (k,l)-Tensorfeld ist eine Abbildung, die jeden Punkt der Mannigfaltigkeit auf einen (k,l)-Tensor abbildet.

Die Koordinatendarstellungen von Tensorfeldern müssen ein bestimmtes Transformationsverhalten unter Kartenwechselabbildungen, also lokalen Diffeomorphismen, erfüllen.

Indexnotation

Die Indexnotation schreibt die Argumente, in denen der Tensor linear ist, nicht mittels einer Argumentklammer sondern mittels Indizes. Diese Indizes werden hoch- oder tiefgestellt, je nachdem ob das Argument aus dem Tangentialraum oder dem Kotangentialraum ist. Ein (k,l)-Tensor T mit Argumenten 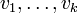$v_1, \ldots, v_k$ aus dem Tangentialraum und 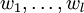$w_1, \ldots, w_l$ aus dem Kotangentialraum wird also notiert als:

$T(v_1, \ldots, v_k,w_1, \ldots, w_l)=T_{\mu_1 \ldots \mu_k}^{\nu_1 \ldots \nu_l} (v_1)^{\mu_1} \ldots (v_k)^{\mu_k} (w_1)_{\nu_1} \ldots (w_l)_{\nu_l}$

Die Indexnotation beruht darauf, dass Tensoren multilineare Abbildungen sind und daher in den Argumenten, in denen sie linear sind, ein Distributivgesetz erfüllen und mit der Multiplikation mit Skalaren kommutieren. Das bedeutet, dass sich z.B. rv₁ + sV₁ mit r und s reellen Zahlen und v₁ und V₁ aus dem Tangentialraum statt v₁ einsetzen lässt und damit wie mit Zahlen weitergerechnet werden kann.

Wenn man die obige Formel als Koordinatenschreibweise versteht, ist sie mit der Summenkonvention einfach zu verstehen. Diese Notation lässt sich jedoch auch koordinatenfrei auffassen, wobei die Position der Indizes nur beschreibt, welche Art Tensor vorliegt, wobei also obenstehende Indizes Kopien des Tangentialraums und untenstehende Indizes Kopien des Kotangentialraums bezeichnen. Das Zeichen für das Tensorprodukte wird in dieser Notation ausgelassen, das heißt hintereinandergeschriebene Tensoren werden als Tensorprodukt aufgefasst. Bei einem einmal oben- und einmal untenstehenden Index wird ein Kontraktion analog zur kanonischen Paarung verstanden, was prinzipiell nicht basisabhängig ist.

Tensoren in der Physik

Ein Tensor ist, im Sprachgebrauch der Physik, eine Äquivalenzklasse von Tripeln (B,S,T), bestehend aus

1. einer Basis B eines fixierten n-dim. Vektorraums V, z. B. des Minkowski-Raumes,
2. einer Signatur S, die ein Tupel einer Länge s mit Einträgen S_k∈{h,t}, k=1,…,s, ist,
3. und einem „Hypertupel“ T, d. h. einer Abbildung T:I^s→ℝ, wobei I={1,2,…,n}.

• Die Länge s der Signatur, die auch die Anzahl der Argumente der Abbildung T angibt, heißt Stufe des Tensors.
• Für die Abbildung T wird nicht die übliche Funktionsschreibweise verwendet, sondern ähnlich wie bei Folgen die alternative (und historisch ältere) Indexschreibweise, wobei Indizes oben und unten hinter dem Funktionssymbol T angeordnet werden können. Welche Indizes oben und welche unten geschrieben werden, gibt die Signatur an. Dabei steht ein Eintrag h oder t in der Signatur für Hoch- und Tiefstellen des entsprechenden Index.
• Zwei Tripel (B,S,T) und (B',S',T') bezeichnen denselben Tensor, wenn die Struktur übereinstimmt, d. h. S=S' , und die Komponenten von T und T' über die Koordinatenwechselmatrix A verbunden sind. Das heißt B=B'A, wenn die Basis als Zeilenvektor der Basisvektoren aufgefasst wird und A eine n×n-Matrix ist. Das Transformationsverhalten hat dann folgende Gestalt

$T'(i_1,\dots,i_s)=$$\sum_{j_1,\dots,j_s} (A^{S_1})(i_1,j_1)\cdot\ldots\cdot(A^{S_s})(i_s,j_s)\cdot T(j_1,\dots,j_s)$

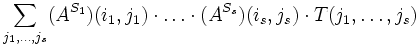
wobei A^h: = A die Transformationsmatrix und A^t: = A ^{− T} die Transponierte der inversen Matrix ist, d. h. 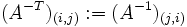$(A^{-T})_{\left(i,j\right)}:=(A^{-1})_{\left(j,i\right)}$. Der Allgemeinheit willen wurde auf das Hoch- und Tiefstellen verzichtet und die Funktionsschreibweise statt der Indizes gewählt, konkrete Beispiele für die Indexschreibweise finden sich weiter unten.

Beziehung zum geometrischen Tensorprodukt

Eine Klasse äquivalenter Darstellungstripel (B,S,T) bezeichnet die Koordinatendarstellung eines Elements aus dem Tensorproduktraum

$\mathcal T^SV=V^{S_1}\otimes\ldots\otimes V^{S_s}$,

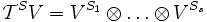wobei V^h: = V der Vektorraum und V^t: = V ^* der duale Vektorraum der Linearformen ist. Das Element selbst ist dann die Summe

$\mathfrak{T}=\sum_{j_1,\dots,j_s} T(j_1,\dots,j_s) \cdot e^{S_1}_{j_1}\otimes \ldots \otimes e^{S_s}_{j_s}$,

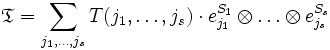mit 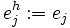$e^h_j:=e_j$ ein Basisvektor und 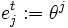$e^t_j:=\theta^j$ ein Element der dualen Basis.

Beispiele

Beispiele der Stufe 1

Beispiel einer kontravarianten Größe ist der Spaltenvektor der Koordinaten eines Ortsvektors (x^μ), als Tripel also (B,(h),x). Kontravariante Größen haben vereinbarungsgemäß immer hochgestellte Indizes. Der Variationsbereich der Indizes entspricht gemäß ihrer Herkunft immer der Basis, hat also eine Anzahl, die der Dimension des Raums entspricht.

Unter einem Basis-/Koordinatenwechsel B=B'A transformiert sich der Vektor als

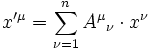$x'^{\mu}=\sum_{\nu=1}^n A^\mu{}_\nu \cdot x^\nu$, d. h. $\vec{x'}=A\vec{x}$.

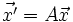Das invariante geometrische Objekt ist der Vektor

$x:=\sum_{\nu=1}^n x^\nu\cdot e_\nu$.

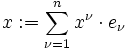In der relativistischen Raum-Zeit werden die Koordinaten als

$x= \left( x^\mu \right) = \left( x^0,x^1,x^2,x^3 \right) ^T= \left( c\, t,x,y,z \right) ^T$

angegeben.

Beispiel einer kovarianten Größe ist der Zeilenvektor der Koordinaten einer 1-Form, d. h. eines linearen Funktionals, α = (α_μ), oder als Tripel (B,(t),α). Kovariante Größen haben vereinbarungsgemäß immer tiefgestellte Indizes. Sie transformieren sich definitionsgemäß nach

$\alpha'_\mu=\sum_{\nu=1}^n (A^{-T})_\mu{}^\nu \cdot \alpha_\nu$

Das invariante geometrische Objekt ist der Kovektor

$\mathbf{\alpha}:=\sum_{\nu=1}^n \alpha_\nu\cdot \theta^\nu$.

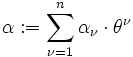In der relativistischen Raum-Zeit werden die Koordinaten als

$\left(\alpha_\mu\right) =\left(\alpha_0,\alpha_1,\alpha_2,\alpha_3\right)$

angegeben.

Analog zur Multiplikation eines Zeilen- mit einem Spaltenvektor in $\mathbb{R}^n$ definiert man die Anwendung eines linearen Funktionals auf einen Vektor:

$\langle\alpha|x\rangle=\mathbf\alpha(x)=\sum_\mu \alpha_\mu x^\mu = \alpha_\mu x^\mu$

Die letzte Schreibweise verwendet die Einsteinsche Summationskonvention, die besagt, dass über gleich benannte Indizes summiert wird, wenn der eine unten und der andere oben steht. Man spricht auch, etwas ungenau, vom Skalarprodukt eines ko- und eines kontravarianten Vektors.

Man rechnet leicht nach, dass es sich dabei auch tatsächlich um einen Skalar, d. h. einen transformationsinvarianten Tensor 0. Stufe handelt:

$\langle\alpha'|x'\rangle =(A^{-T})_\mu{}^\nu\alpha_\nu\cdot A^\mu{}_\kappa x^\kappa =(A^{-1})^\nu{}_\mu A^\mu{}_\kappa \cdot \alpha_\nu x^\kappa =\delta^\nu{}_\kappa \alpha_\nu x^\kappa= \langle\alpha|x\rangle$

Beispiele der Stufe 2

Es findet sehr oft eine Umschreibung kontravarianter Koordinaten in kovariante statt, d. h. eine Umwandlung eines Vektors in eine 1-Form und umgekehrt. Man bezeichnet dies als Hochstellen oder Herunterstellen von Indizes.

Dies wird durch einen metrischen Tensor g ermöglicht, ein Tensor der Stufe (0,2) mit zweifach kovarianten Koordinaten g_μν. D.h. ihm entspricht das Tupel (B,(t,t),g) und die Transformationsvorschrift

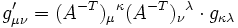$g'_{\mu\nu}=(A^{-T})_\mu{}^\kappa(A^{-T})_\nu{}^\lambda\cdot g_{\kappa\lambda}$ und das geometrische invariante Objekt

$\mathbf g=g_{\mu\nu}\cdot \theta^\mu\otimes\theta^\nu$.

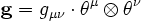Im Allgemeinen verlangt man, dass der metrische Tensor symmetrisch – g(x,y)=g(y,x) bzw. g_μν = g_νμ – und nicht ausgeartet ist, d. h. es muss einen inversen symmetrischen Tensor g^-1 der Stufe (2,0) geben, welcher kontravariante Koordinaten g^μν hat, so dass gilt:

$g_{\mu\kappa}g^{\kappa\nu} = \delta_\mu^\nu = \begin{cases}1&\mbox{ bei }\mu=\nu\\0&\mbox{ bei }\mu\ne\nu\end{cases}.$.

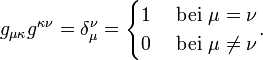Die Inverse zum metrischen Tensor wird auch als seine kontravariante Form bezeichnet.

Die adjungierte 1-Form des Ortsvektors x hat dann die „gesenkten“ Koordinaten

x_μ = g_μνx^ν, umgekehrt ist x^μ = g^μνx_ν.

Die Anwendung der adjungierten 1-Form (x_μ) auf den Ortsvektor (x^μ)

g(x,x) = g_μνx^μx^ν = x_μx^μ = x₀x⁰ + x₁x¹ + x₂x² + x₃x³

ist eine quadratische Abbildung, die den Ortsvektor auf eine reelle Zahl abbildet.

Der Vektor (x^k) wurde bereits durch die Kartesischen Koordinaten x,y,z und die Zeitkoordinate ct ausgedrückt.

In der Speziellen Relativitätstheorie bzw. im Minkowski-Raum ist die Koordinatenmatrix des metrischen Tensors diagonal mit Einträgen (1,-1,-1,-1) auf der Diagonalen, es werden als Koordinaten-/Basistransformationen nur sog. Lorentz-Transformationen zugelassen, welche diese Normalform des metrischen Tensors unverändert lassen. Der entsprechende adjungierte kovariante Vektor lautet in diesen Koordinaten:

(x_k)=(ct,-x,-y,-z)

Hieraus folgt: g(x,x) = x_kx^k = c²t² − x² − y² − z². Man beachte, dass die scheinbare Einfachheit dieser Formel eine komplexe Konstruktion verbirgt: Der Vektor x wird in zwei verschiedenen Koordinatendarstellungen ausgedrückt, wobei in eine der Metrik-Tensor schon eingegangen ist. Die übliche Koordinatendarstellung eines Skalarproduktes hat zwar dieselbe Komplexität, aber verbirgt diese nicht.

Durch die kontravariante und kovariante Schreibweise werden Darstellungen in der Form (x,y,z,ict) mit der imaginären Einheit i vermieden, wie sie früher gebräuchlich waren und auch heute noch in manchen Lehrbüchern verwendet werden.

Darüber hinaus ermöglicht ihre Verwendung in der Speziellen Relativitätstheorie den direkten Übergang auf den Allgemeinen Fall.