Eisensteinzahl

Eisenstein-Zahlen als Punkte eines Dreiecksgitters in der komplexen Zahlenebene

Die Eisenstein-Zahlen sind eine Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen. Sie sind nach dem deutschen Mathematiker Gotthold Eisenstein, einem Schüler von Gauß benannt. Die Gaußschen Zahlen sind eine andere Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen. Die Eisenstein-Zahlen sind der Ganzheitsring des quadratischen Zahlkörpers 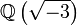$\mathbb{Q}\left(\sqrt{-3} \right)$. Sie treten beispielsweise bei der Formulierung des kubischen Reziprozitätsgesetzes auf.

Definition

Eine komplexe Zahl E ist eine Eisenstein-Zahl, wenn sie sich in der Form

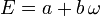$E = a + b\,\omega$ mit $\omega = e^{2\pi\mathrm i/3} =-\frac12+\frac{\mathrm i}2\sqrt3$

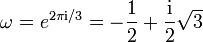
und ganzen Zahlen a und b darstellen lässt. ω ist eine (primitive) dritte Einheitswurzel und erfüllt somit die Gleichung

ω² + ω + 1 = 0.

Eigenschaften und Bedeutung

Die Eisenstein-Zahlen bilden ein Dreiecksgitter in der gaußschen Zahlenebene. Sie entsprechen den Mittelpunkten einer dichtesten Kugelpackung in zwei Dimensionen.

Auf den Eisenstein-Zahlen lässt sich Zahlentheorie betreiben. Man kann Primelemente (analog zu den Primzahlen in $\mathbb{Z}$) definieren und zeigen, dass die Primfaktordarstellung einer Eisenstein-Zahl eindeutig ist. Ganze Zahlen der Form m² + 3n² sind in den Eisenstein-Zahlen immer zerlegbar. Daher sind die Zahlen 3, 7, 13, 19, ... keine Primelemente in den Eisenstein-Zahlen.

Weblinks

• Eisenstein-Zahlen bei MathWorld (englisch)