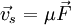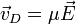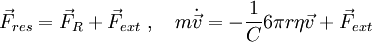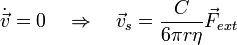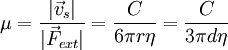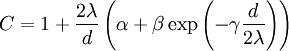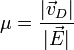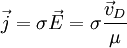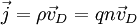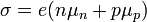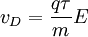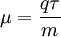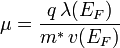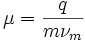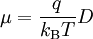Elektronenbeweglichkeit

Die Beweglichkeit bzw. Mobilität μ als physikalischer Begriff ist definiert über die konstante Geschwindigkeit 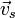$\vec{v}_{s}$, welche ein Körper (asymptotisch) erreicht, wenn an ihn eine konstante Kraft 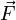$\vec{F}$ angreift.

$\vec{v}_{s}=\mu\vec{F}$

In der Elektrodynamik wird die Beweglichkeit in leicht abgewandelter Form definiert. Die Ladungsträgermobilität, meist einfach Mobilität genannt, bezeichnet den Zusammenhang zwischen der Driftgeschwindigkeit von Ladungsträgern und einem angelegten elektrischen Feld:

$\vec{v}_{D}=\mu\vec{E}$

Grundsätzlich ist es nur in dissipativen Systemen sinnvoll eine Mobilität einzuführen, also dort wo es Reibung, inelastische Streuung gibt. Ab einer bestimmten Geschwindigkeit gibt es ein Gleichgewicht zwischen äußerer Kraft und entgegengesetzt wirkender Reibungskraft, sodass die Bewegung stationär ist (allgemeiner: die mittlere Geschwindigkeit ist stationär).

Beweglichkeit in der Mechanik

Eine konstante an einem Körper angreifende Kraft 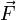${\vec F}$ bewirkt solange dessen Beschleunigung, bis die entgegengesetzte Reibungskraft (z. B. Luft- oder Gleitreibung) den gleichen Betrag hat. Dann ist die stationäre Geschwindigkeit 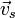$\vec{v}_{s}$ erreicht und die effektive Beschleunigung beträgt null. Dies ist z. B. der Grund, warum ein in der Atmosphäre fallender Körper nicht beliebig schnell wird. Eine Ursache dieser Gesetzmäßigkeit ist die Abhängigkeit der Reibung von der Geschwindigkeit des Körpers.

Die mechanische Beweglichkeit μ ist daher definiert als

$\mu = \frac{|\vec{v}_{s}|}{|\vec{F}|}$.

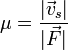In der Mechanik hat die Beweglichkeit somit die Einheit s/kg. Historisch interessant ist, dass Aristoteles dieses Gesetz als grundlegend für seine Mechanik angenommen hat. Die heutige Mechanik hingegen beruht auf den Newtonschen Axiomen, aus denen das Gesetz hervorgeht.

Mobilität bei Stokes'scher Reibung

Ein Körper werde durch eine externe Kraft beschleunigt und durch Stokes'sche Reibung gebremst. Die resultierende Kraft setzt sich aus diesen beiden Beiträgen zusammen:

$\vec{F}_{res}=\vec{F}_{R}+\vec{F}_{ext}\ ,\quad m\dot{\vec{v}}=-\frac{1}{C}6\pi r\eta\vec{v}+\vec{F}_{ext}$

Im Gleichgewicht ist die resultierende Kraft und somit die Beschleunigung gleich Null und die stationäre Geschwindigkeit ist erreicht:

$\dot{\vec{v}}=0\quad\Rightarrow\quad\vec{v}_{s}=\frac{C}{6\pi r\eta}\vec{F}_{ext}$

Die Beweglichkeit ist also

$\mu=\frac{|\vec{v}_{s}|}{|\vec{F}_{ext}|}=\frac{C}{6\pi r\eta}=\frac{C}{3\pi d\eta}$

Mobilitätsdurchmesser

Die Beweglichkeit eines sich in einer Flüssigkeit bewegenden Körpers kann auch durch den mobilitätsäquivalenten Durchmesser bzw. Mobilitätsdurchmesser ausgedrückt werden. Dies ist der Durchmesser d einer Kugel, welche diese Mobilität besitzt. Sein Wert ist nach dem stokesschen Gesetz 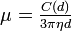$\mu = \tfrac{C(d)}{3 \pi \eta d}$, wobei der Cunningham-Korrekturfaktor C angibt, ob das den Körper umgebende Fluid als Kontinuum aufgefasst werden kann, als freimolekular oder dazwischen. Ausschlaggebend ist dabei die mittlere Freie Weglänge der Fluidmoleküle λ und der Mobilitätsdurchmesser des Körpers d.

$C = 1 + \frac{2 \lambda}{d} \left(\alpha + \beta \exp\left(-\gamma \frac{d}{2 \lambda}\right)\right)$

Die Konstanten α, β und γ wurden empirisch ermittelt und werden i.d.R. als allgemeingültig betrachtet.

Anwendung findet diese Größe vor allem in der Aerosoltechnik, besonders für ultrafeine Partikel.

Beweglichkeit in der Elektrodynamik

In der Elektrodynamik wird die Beweglichkeit in leicht abgewandelter Form definiert. Die Ladungsträgermobilität (oder einfach Mobilität, speziell für Elektronen: Elektronenmobilität) bezeichnet den Zusammenhang zwischen einem angelegten elektrischen Feld und der Driftgeschwindigkeit von Ladungsträgern (Festkörper: Defekt-/Elektronen, Plasma: Elektronen/Ionen).

$\mu = \frac{|\vec{v}_{D}|}{ |\vec{E}|}$

wobei μ die Einheit 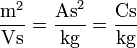  $\frac{\mathrm{m}^2}{\mathrm{Vs}} = \frac{\mathrm{As}^2}{\mathrm{kg}} = \frac{\mathrm{Cs}}{\mathrm{kg}}$   hat. Gewöhnlich wird die Mobilität in cm²/(V·s) angegeben.

Während bei kleinen Feldstärken  μ  unabhängig von der Feldstärke ist, muss letztere bei hohen Feldstärken berücksichtigt werden. Das genaue Verhalten wird dabei wesentlich durch das Material beeinflusst, also z. B. dadurch, ob ein elektrischer Strom durch einen Festkörper oder ein Plasma fließt. Bei sehr großen Feldstärken erhöht sich in Festkörpern die mittlere Elektronengeschwindigkeit nicht mehr und erreicht die Sättigungsgeschwindigkeit v_sat.

Zusammenhang mit Leitfähigkeit

Die elektrische Leitfähigkeit lässt sich mit der Beweglichkeit in Verbindung bringen. Für leitfähige Stoffe lautet die Materialgleichung, die die elektrische Stromdichte mit dem angelegten elektrischen Feld über die elektrische Leitfähigkeit σ verknüpft:

$\vec{j} = \sigma \vec{E} = \sigma \frac{\vec{v}_{D}}{\mu}$

Das zweite Gleichheitszeichen gilt unter Verwendung der obigen Definition der Beweglichkeit. Allgemein ist die Stromdichte als Ladungsdichte mal Geschwindigkeit definiert (ρ = qn  ist die Ladungsdichte = Ladung mal Ladungsträgerdichte):

$\vec{j} = \rho \vec{v}_{D} = q n \vec{v}_{D}$

Somit kommt man durch Gleichsetzen auf den Zusammenhang zwischen Leitfähigkeit und Beweglichkeit:

$\, \sigma = q n \mu$,

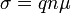wobei q  die elektrische Ladung (nicht notwendigerweise die Elementarladung) eines Ladungsträgers (z. B. Elektron, Loch, Ion, geladenes Molekül etc.) und n die Ladungsträgerdichte darstellen. In Metallen ändert sich die Ladungsträgerdichte mit der Temperatur wenig und die Leitfähigkeit ist von der temperaturabhängigen Mobilität bestimmt

Die Leitfähigkeit eines Halbleiters setzt sich zusammen aus der Elektronendichte n und deren Beweglichkeit μ_n sowie der Lochdichte p und deren Beweglichkeit μ_p

$\, \sigma = e (n \mu_n + p \mu_p)$

Bei Halbleitern ändert sich mit der Temperatur die Ladungsträgerdichte stark (exponentiell), dagegen ist die Temperaturabhängigkeit der Mobilität klein.

Mikroskopische Betrachtung

Ladungsträger bewegen sich in einem Gas oder Festkörper ohne ein elektrisches Feld in der Regel zufällig, d. h. die Driftgeschwindigkeit ist null. Bei Anwesenheit eines elektrischen Feldes bewegen sich die Ladungen dagegen mit einer effektiven Geschwindigkeit entlang des Feldes, die deutlich geringer als die mittlere Geschwindigkeit der einzelnen Ladungen ist.

Nach dem Drude-Modell ist die Driftgeschwindigkeit gleich

$v_D = \frac{q \tau}{m} E$

Daraus kann man die Mobilität direkt ablesen:

$\mu = \frac{q \tau}{m}$

wobei q: Ladung, m Masse, τ mittlere Stoßzeit (Zeit zwischen zwei Stößen). Die mittlere Stoßzeit lässt sich als Quotient aus mittlerer freier Weglänge und mittlerer Geschwindigkeit schreiben:

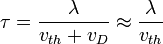$\tau = \frac{\lambda}{v_{th}+v_{D}} \approx \frac{\lambda}{v_{th}}$   mit   $v_{th} = \sqrt{\frac{3kT}{m}}$

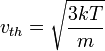
Die mittlere Geschwindigkeit setzt sich aus mittlerer thermischer Geschwindigkeit und Diftgeschwindigkeit zusammen. Die Driftgeschwindigkeit ist bei nicht zu großen elektrischen Feldstärken viel kleiner als die thermische Geschwindigkeit, weswegen man sie vernachlässigen kann.

Eine quantenmechanische Betrachtung nach Sommerfeld liefert ein ähnliches Ergebnis. Dort muss allerdings die Masse durch die effektive Masse (kann sich um mehrere Größenordnungen von der Elektronenmasse unterscheiden) ersetzt werden. Zudem muss die mittlere Stoßzeit für die Elektronen mit der Fermienergie eingesetzt werden. Zur Leitfähigkeit (in entarteten Systemen, wie Metallen und hochdotierten Halbleitern) tragen nämlich nur die Elektronen mit Energie im Bereich kT um die Fermienergie bei.

$\mu = \frac{q\, \lambda(E_{F})}{m^{*}\, v(E_{F})}$

Mobilität in Festkörpern

Bei Festkörpern hängt die Mobilität stark von der Anzahl von Störstellen und der Temperatur ab, sodass es schwierig ist Werte anzugeben. Es ist zu beachten, dass im Gegensatz zu einem einzigen Körper die Geschwindigkeit der vielen vorhandenen Ladungsträger statistisch verteilt ist. Die notwendige Reibungskraft, die eine konstante Beschleunigung verhindert, ist durch die Streuung an Fehlstellen im Kristall und an Phononen gegeben. Die mittlere freie Weglänge wird von diesen beiden Streumechanismen begrenzt. Die Elektronen untereinander streuen nur sehr selten und an den Gitteratomen eigentlich gar nicht. Näherungsweise lässt sich die Mobilität als Kombination von Effekten von Gitterschwingungen (Phononen) und von Störstellen durch die folgende Gleichung ausdrücken (Matthiessensche Regel):

$\mu = \frac{1}{\frac{1}{\mu_{\rm Gitter}}+\frac{1}{\mu_{\rm St\ddot{o}rstellen}}}$.

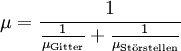Die Mobilität ist abhängig vom Material, der Störstellendichte, der Temperatur und der Feldstärke. Bei niedrigen Temperaturen streuen die Elektronen hauptsächlich mit Störstellen, bei höheren verstärkt mit Phononen (je höher die Temperatur, desto mehr Phononen sind angeregt).

Wie die quantenmechanische Betrachtung nach Sommerfeld zeigt, ist die Mobilität von der effektiven Masse abhängig. Dabei ist zu beachten, dass die effektive Masse im Allgemeinen ein Tensor, also richtungsabhängig ist. Somit ist bei einkristallinen Materialien die Beweglichkeit von der Kristallorientierung abhängig.

In Halbleitern ist die Mobilität zudem unterschiedlich für Elektronen im Leitungsband und Defektelektronen (= Löcher) im Valenzband. Elektronen haben meist kleinere effektive Massen als Löcher und somit eine höhere Mobilität. Falls einer der beiden Ladungsträger durch Dotierung dominiert, so ist die Leitfähigkeit des Halbleiters proportional zur Mobilität der Majoritätsladungsträger. Durch Dotierung eines hochreinen Halbleitermaterials (typischerweise Silizium) durch Fremdatome geeigneter Natur werden gezielt eine bestimmte Menge von beweglichen Ladungsträgern eingebracht. Je nach Dotierungsmaterial entstehen Überschuss-Elektronen (n-Dotierung) oder Elektronenfehlstellen (p-Dotierung).

Ladungsträgermobilität einiger Stoffe

Abhängig von der Materialstruktur kann die Beweglichkeit stark variieren. Beispielsweise erreicht sie im Standardmaterial der Elektronik, dem Silicium (Si), nur mittlere Werte. Im Galliumarsenid (GaAs) dagegen ist sie wesentlich höher, mit der Folge, dass dieses Material weit höhere Arbeitsfrequenzen aus ihm erstellter Bauteile zulässt als Silicium, das aber zu ebenfalls höheren Materialkosten.

Material	Elektronenmobilität	Löchermobilität	Anmerkungen
organische Halbleiter	≤ 10 cm2·V-1·s-1		bei 300 K
Silizium	1.400 cm2·V-1·s-1	450 cm2·V-1·s-1	bei 300 K
Germanium	3.900 cm2·V-1·s-1	1.900 cm2·V-1·s-1	bei 300 K
Galliumarsenid	9.200 cm2·V-1·s-1	400 cm2·V-1·s-1	bei 300 K
Indiumantimonid	77.000 cm2·V-1·s-1		bei 300 K
Kohlenstoff-Nanoröhrchen	100.000 cm2·V-1·s-1		bei 300 K
Graphen	10.000 cm2·V-1·s-1		bei 300 K; auf SiO2-Träger
Graphen	200.000 cm2·V-1·s-1		bei 300 K; theoretischer Maximalwert
Zweidimensionales Elektronengas	3.000.000 cm2·V-1·s-1		nahe dem absoluten Nullpunkt

Mobilität in der Gasphase

Mobilität wird für jeden Bestandteil der Gasphase einzeln definiert. Dies ist von besonderem Interesse in der Plasmaphysik. Die Definition lautet:

$\mu = \frac{q}{m\nu_m}$

wobei q - Ladung des Bestandteils, ν_m - Stoßfrequenz, m - Masse.

Der Zusammenhang zwischen der Mobilität und dem Diffusionskoeffizienten ist als Einstein-Gleichung bekannt:

$\mu = \frac{q}{k_\mathrm{B}T}D$

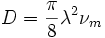wobei $D = \frac{\pi}{8}\lambda^2 \nu_m$ die Diffusionskonstante, λ die mittlere freie Weglänge, k_B die Boltzmannkonstante und T die Temperatur bezeichnen.

Siehe auch

• Leiter (Physik), Reibung

Weblinks

• semiconductor glossary
• Bart Van Zeghbroeck's Online Book Principles of Semiconductor Devices