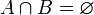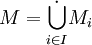- Elementfremd
-
In der Mengenlehre heißen zwei Mengen A und B disjunkt (lat: disiunctum: getrennt) oder elementfremd, wenn sie kein gemeinsames Element besitzen. Mehrere Mengen heißen paarweise disjunkt, wenn je zwei von ihnen disjunkt sind.
Inhaltsverzeichnis
Definitionen
Zwei Mengen A und B sind disjunkt, wenn ihre Schnittmenge leer ist, wenn also gilt:
Eine Familie
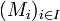 von Mengen ist eine disjunkte Mengenfamilie, wenn ihre Elemente paarweise disjunkt sind, wenn also gilt:
von Mengen ist eine disjunkte Mengenfamilie, wenn ihre Elemente paarweise disjunkt sind, wenn also gilt: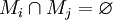 für
für 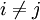
Die Vereinigung M einer disjunkten Mengenfamilie nennt man disjunkte Vereinigung und schreibt sie als
Sind außerdem alle Mengen der Familie nichtleer, liegt eine Partition von M vor.
Die Begriffe werden auch analog für Mengensysteme (anstelle von Mengenfamilien) verwendet.
Beispiele
- Die Mengen A = {1,2,3} und B = {7,8,11} sind disjunkt, weil sie kein gemeinsames Element haben.
- Die Mengen A = {1,2,7} und B = {6,7,8,11} sind nicht disjunkt, da sie das Element 7 gemeinsam haben.
- Die drei Mengen A = {1,2,3}, B = {4,5} und C = {5,6,7} sind nicht paarweise disjunkt, da zumindest eine der drei möglichen Schnittmengen (nämlich
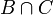 ) nichtleer ist.
) nichtleer ist.
- Die folgende Aufzählung definierte eine (unendliche) disjunkte Mengenfamilie, die eine Partition der ganzen Zahlen darstellt:
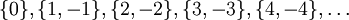 .
.
- Zwei verschiedene Geraden g und h in der euklidischen Ebene sind genau dann disjunkt, wenn sie parallel sind. Die Gesamtheit aller Parallelen zu einer gegebenen Geraden g bildet eine Partition der Ebene.
Eigenschaften
- Die leere Menge
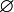 ist disjunkt zu jeder beliebigen Menge.
ist disjunkt zu jeder beliebigen Menge.
- {a} und B sind genau dann disjunkt, wenn
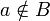 .
.
- Die Mächtigkeit einer endlichen disjunkten Vereinigung endlicher Mengen ist gleich der Summe der Einzelmächtigkeiten. Für nicht-disjunkte Vereinigungen gilt die Siebformel.
Siehe auch
- Lineare Disjunktheit, ein Begriff der abstrakten Algebra im Zusammenhang mit Körpererweiterungen, der mit der hier betrachteten Disjunktheit nur gemeinsam hat, dass die Schnittmenge linear disjunkter Körper kleinstmöglich ist.
Weblinks
Wikimedia Foundation.