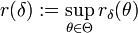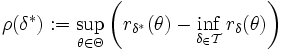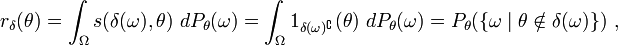Entscheidungsfunktion

Ein allgemeiner Test oder Entscheidungsverfahren ist ein abstraktes Instrument der mathematischen Statistik. Fast alle statistischen Tests, wie bspw. Hypothesentests oder Parameterpunktschätzungen, lassen sich in der Form eines allgemeinen Tests mathematisch erfassen. Ziel eines allgemeinen Tests ist es aufgrund der (beobachteten) Realisation einer oder mehrerer zuvor definierter Zufallsgrößen, deren genaue Wahrscheinlichkeitsverteilung i.d.R. nicht bekannt ist, bzgl. einer betrachteten Fragestellung eine Entscheidung zu treffen.

Beispiel: Ein Pharmaunternehmen möchte ein neu entwickeltes Medikament auf seine (unbekannte) Wirksamkeit testen. Hierfür bekommt eine bestimmte Anzahl von Patienten das Medikament verabreicht. Aufgrund der gemessenen Wirkung des Medikaments auf die Patienten muss sich das Pharmaunternehmen nun entscheiden, ob man das neue Medikament auf dem Markt einführt oder lieber weiter auf ein alt bewährtes Medikament zurückgreift.

Entscheidet sich das Pharmaunternehmen für die Markteinführung des neues Medikaments, so besteht die Gefahr, dass dieses durch das verwendete Entscheidungsverfahren nur fälschlicherweise als besser als das alte Medikament eingestuft wurde. In diesem Fall entstünde dem Pharmaunternehmen ein unnötiger Schaden. Um einen solchen zu vermeiden liegt jedem allgemeinen Test eine sog. Schadensfunktion zugrunde, mit Hilfe derer man versucht durch die Wahl einer "geeigneten" Entscheidungsfunktion das Risiko einer Entscheidung zu minimieren.

Definition

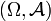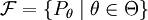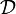Gegeben sei ein Messraum $(\Omega,\mathcal A)$ und eine Familie von Wahrscheinlichkeitsmaßen $\mathcal F=\{P_\theta\mid \theta\in\Theta\}$ auf $\mathcal A$. Ω umfasst hierbei gerade alle möglichen Realisationen oder Beobachtungen. Weiter sei $\mathcal D$ eine Menge von möglichen Entscheidungen.

• Eine Abbildung 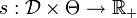$s:\mathcal D\times\Theta\to\mathbb R_+$ heißt Schadensfunktion.

• Eine Abbildung 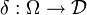$\delta:\Omega\to\mathcal D$ heißt genau dann allgemeiner Test, Entscheidungsfunktion oder auch Entscheidungsverfahren, wenn für jedes 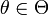$\theta\in\Theta$ die Abbildung 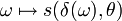$\omega\mapsto s(\delta(\omega),\theta)$ gerade 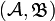$(\mathcal A,\mathfrak B)$-messbar ist. Hierbei bezeichnet 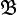$\mathfrak B$ die Borelsche σ-Algebra über $\mathbb R$.

Gütekriterien

Risiko

Es sei 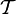$\mathcal T$ eine Klasse von Entscheidungsfunktionen. Für eine Element 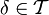$\delta\in\mathcal T$ bezeichnet man

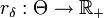$r_\delta:\Theta\to\mathbb R_+$ vermöge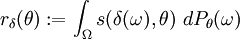 $r_\delta(\theta):=\int_\Omega s(\delta(\omega),\theta)\ dP_\theta(\omega)$

als Risikofunktion. Diese gibt an, welcher Schaden durch die Anwendung des Tests δ im Mittel unter der Verteilung P_θ entsteht. Wegen 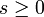$s\geq0$ existiert diese immer, evtl. jedoch uneigentlich. Weiter bezeichnet man

$r(\delta):=\sup_{\theta\in\Theta} r_\delta(\theta)$

als das Risiko von δ.

Hat man nun weiter eine σ-Algebra 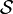$\mathcal S$ über Θ und ein Wahrscheinlichkeitsmaß μ auf 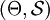$(\Theta,\mathcal S)$ gegeben, so definiert μ eine a-priori-Verteilung oder (subjektive) Vorbewertung auf der Parametermenge. Ist die Risikofunktion 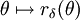$\theta\mapsto r_\delta(\theta)$ messbar bzgl. 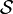$\mathcal S$, so lässt sich hiermit das sog. Bayesrisiko des Tests δ bzgl. μ einführen, und zwar setzt man dann

$r_\delta(\mu):=\int_\Theta r_\delta(\theta)\ d\mu(\theta)$.

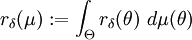Effizienz

Mit Hilfe des Risikos und der Risikofunktion lassen sich nun zwei allgemeine Tests 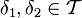$\delta_1,\delta_2\in\mathcal T$ miteinander vergleichen. Man sagt δ₁ ist mindestens so effizient wie δ₂, wenn

$r_{\delta_1}(\theta)\leq r_{\delta_2}(\theta)\quad \forall \theta\in\Theta$.

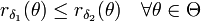Im Falle einer Vorbewertung μ lassen sich die Tests außerdem mit Hilfe des Bayesrisikos vergleichen. Man sagt dann δ₁ ist mindestens so effizient wie δ₂, wenn $r_{\delta_1}(\mu)\leq r_{\delta_2}(\mu)$.

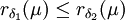Optimalität

Die Optimalität eines Tests lässt sich auf verschiedenste Weisen einführen. Man bezeichnet einen Test 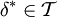$\delta^*\in\mathcal T$ als

• höchsteffizient in 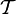$\mathcal T$, wenn 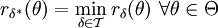$r_{\delta^*}(\theta)=\min_{\delta\in\mathcal T} r_\delta(\theta)\ \forall\theta\in\Theta$ gilt.
• Minimaxverfahren in 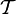$\mathcal T$, wenn 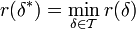$r(\delta^*)=\min_{\delta\in\mathcal T} r(\delta)$ gilt.
• Bayeslösung in 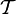$\mathcal T$ bzgl. μ, wenn 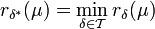$r_{\delta^*}(\mu)=\min_{\delta\in\mathcal T} r_\delta(\mu)$ gilt.
• multisubjektiv optimal oder 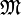$\mathfrak M$-Minimaxverfahren in 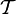$\mathcal T$, wenn 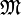$\mathfrak M$ eine Familie von Wahrscheinlichkeitsmaßen auf 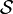$\mathcal S$ ist und gilt $\sup_{\mu\in\mathfrak M} r_{\delta^*}(\mu)=\min_{\delta\in\mathcal T}\sup_{\mu\in\mathfrak M}r_\delta(\mu)$.

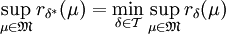Bei festem Parameter θ ist 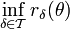$\inf_{\delta\in\mathcal T}r_\delta(\theta)$ der unvermeidbare Schaden für jeden Test in 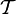$\mathcal T$. Für einen guten Test wird man deshalb verlangen, dass

$\rho(\delta^*):=\sup_{\theta\in\Theta}\left(r_{\delta^*}(\theta)-\inf_{\delta_\in\mathcal T}r_\delta(\theta)\right)$

möglichst klein wird ("minimal regret"). Deshalb bezeichnet man δ ^* weiter als

• strengsten Test in 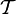$\mathcal T$, wenn 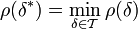$\rho(\delta^*)=\min_{\delta\in\mathcal T}\rho(\delta)$ gilt.

Zusammenhang: Bei den hier aufgeführten Optimalitätskriterien lässt sich die Höchsteffizienz als stärkste Forderung einstufen, denn ist ein Test δ ^* höchsteffizient in 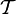$\mathcal T$, so ist er bereits Minimaxverfahren, Bayeslösung, multisubjektiv optimal und auch strengster Test.

Beispiele

Hypothesentest

Bei einem Hypothesen- oder Signifikanztest betrachtet man zwei sich gegenseitig ausschließende Hypothesen H₀ und H₁, von denen man in der Regel eine, bspw. H₀, versucht aufgrund einer Beobachtung 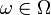$\omega\in\Omega$ zu verwerfen. Die Menge der möglichen Entscheidungen ist deshalb von der Form 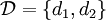$\mathcal D=\{d_1,d_2\}$, wobei man definiert:

d₁: = "Hypothese H₀ kann verworfen werden."

d₂: = "Hypothese H₀ kann nicht verworfen werden, es lässt sich also keine Folgerung aus dem Experiment ziehen."

Parameterpunktschätzung

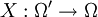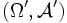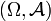Gegeben sei eine Zufallsgröße $X:\Omega'\to\Omega$ bzgl. zweier Messräume $(\Omega',\mathcal A')$ und $(\Omega,\mathcal A)$, die der Verteilungsfamilie 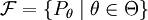$\mathcal F=\{P_\theta\mid\theta\in\Theta\}$ unterliegt. Unbekannt sei hierbei der "wahre" Parameter θ. Diesen, bzw. allgemeiner einen von θ abhängenden Wert λ(θ), gilt es zu schätzen. Als Entscheidungsraum betrachtet man deshalb 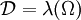$\mathcal D=\lambda(\Omega)$. Als Schadensfunktion verwendet man häufig

$s:\mathcal D\times\Theta\to\mathbb R_+,\ s(d,\theta)=(d-\lambda(\theta))^2$.

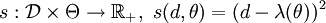Damit ergibt sich für einen Test 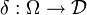$\delta:\Omega\to\mathcal D$ als Risikofunktion die mittlere quadratische Abweichung der Schätzung von dem zu schätzenden Wert, denn

$r_\delta(\theta)=\int_\Omega s(\delta(\omega),\theta)\ dP_\theta(\omega)=\mathbb E_\theta((\delta(X)-\lambda(\theta))^2)$.

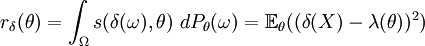Parameterbereichsschätzung

Betrachtet wird wieder die Zufallsgröße X. Schätzen möchte man einen Bereich, in dem man den "wahren" Parameter θ vermutet. Man setzt hierfür 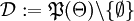$\mathcal D:=\mathfrak P(\Theta)\backslash\{\emptyset\}$. Die Leere Menge schließt man als Entscheidung aus, da das Schätzen dieser nicht sinnvoll wäre. 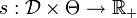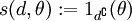Als Schadensfunktion bietet sich die Abbildung $s:\mathcal D\times\Theta\to\mathbb R_+$ mit $s(d,\theta):=1_{d^\complement}(\theta)$ an. Mit ihr erhält man für einen Test 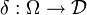$\delta:\Omega\to\mathcal D$ die Risikofunktion

$r_\delta(\theta)=\int_\Omega s(\delta(\omega),\theta)\ dP_\theta(\omega)= \int_\Omega 1_{\delta(\omega)^\complement} (\theta)\ dP_\theta(\omega)= P_\theta(\{\omega\mid\theta\notin\delta(\omega)\})\ ,$

d.h. r_δ(θ) ist gerade die Wahrscheinlichkeit, mit welcher der Paramater θ nicht in der geschätzten Menge liegt. Man nennt r_δ(θ) deshalb auch die Irrtumswahrscheinlichkeit des Verfahrens δ für den Parameter θ. Das Risiko 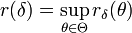$r(\delta)=\sup_{\theta\in\Theta} r_\delta(\theta)$ bezeichnet man als Signifikanzschranke von δ.