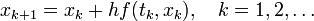Explizites Euler Verfahren
- Explizites Euler Verfahren
-
Das eulersche Polygonzugverfahren oder explizite Euler-Verfahren (auch Euler-Cauchy-Verfahren) ist das einfachste Verfahren zur numerischen Lösung eines Anfangswertproblems.
Es wurde von Leonhard Euler 1768 in seinem Buch Institutiones Calculi Integralis vorgestellt. Cauchy benutzte es, um einige Eindeutigkeitsresultate für gewöhnliche Differentialgleichungen zu beweisen.
Das Verfahren
Zur numerischen Lösung des Anfangswert-Problems:

für eine gewöhnliche Differentialgleichung wähle man eine Diskretisierungs-Schrittweite h > 0, betrachte die diskreten Zeitpunkte

und berechne die iterierten Werte
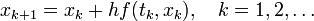
Die berechneten Werte xk stellen Approximationen an die tatsächlichen Werte x(tk) der exakten Lösung des Anfangswert-Problems dar. Je kleiner die Schrittweite h gewählt ist, desto mehr Rechenarbeit ist nötig, aber desto genauer werden auch die approximierten Werte.
Eine Modifikation des Verfahrens besteht hier darin, dass man die Schrittweite variabel wählt. Eine sinnvolle Veränderung der Schrittweite setzt einen Algorithmus zur Schrittweiten-Steuerung voraus, der den Fehler im aktuellen Schritt abschätzt und dann die Schrittweite für den nächsten Schritt dementsprechend wählt.
Wird ein Verfahren über xk + 1 = xk + hf(tk + 1,xk + 1) definiert, erhält man das implizite Euler-Verfahren.
Eigenschaften
Das explizite Euler-Verfahren hat Konsistenz- und Konvergenzordnung 1. Sein Stabilitätsgebiet ist der Kreis um -1 mit Radius 1 in der komplexen Zahlenebene.
Verallgemeinerungen
Es lässt sich im Wesentlichen durch zwei verschiedene Ideen auf effizientere Verfahren verallgemeinern.
- Die erste Idee ist, bei der Berechnung des nächsten Schrittes mehr als nur einen der zuvor berechneten Werte mit einzubeziehen. Auf diese Weise erhält man Verfahren höherer Ordnung in der Klasse der linearen Mehrschrittverfahren.
- Die zweite Idee ist, bei der Berechnung des nächsten Schrittes die Funktion f(t,x) auf dem Intervall [tk,tk + 1] an mehreren Stellen auszuwerten. Auf diese Weise erhält man die Klasse der Runge-Kutta-Verfahren.
Die Klasse der allgemeinen linearen Verfahren bezieht beide Ideen der Verallgemeinerung mit ein und enthält die Klasse der linearen Mehrschrittverfahren sowie die Klasse der Runge-Kutta-Verfahren als Spezialfall.
Literatur
- E. Hairer, S.P. Norsett, G. Wanner: Solving Ordinary Differential Equations I, Springer Verlag
- M. Hermann: Numerik gewöhnlicher Differentialgleichungen, Anfangs- und Randwertprobleme, Oldenbourg Verlag, München und Wien, 2004, ISBN 3-486-27606-9
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Explizites Euler-Verfahren — Das eulersche Polygonzugverfahren oder explizite Euler Verfahren (auch Euler Cauchy Verfahren) ist das einfachste Verfahren zur numerischen Lösung eines Anfangswertproblems. Es wurde von Leonhard Euler 1768 in seinem Buch Institutiones Calculi… … Deutsch Wikipedia
Euler-Maruyama-Schema — Das Euler Maruyama Verfahren, oft auch Euler Maruyama Schema oder stochastisches Euler Schema genannt, ist das einfachste Verfahren zur numerischen Lösung von stochastischen Differentialgleichungen. Es wurde erstmals in den 1950er Jahren durch… … Deutsch Wikipedia
Explizites Eulerverfahren — Das eulersche Polygonzugverfahren oder explizite Euler Verfahren (auch Euler Cauchy Verfahren) ist das einfachste Verfahren zur numerischen Lösung eines Anfangswertproblems. Es wurde von Leonhard Euler 1768 in seinem Buch Institutiones Calculi… … Deutsch Wikipedia
Implizite Euler-Methode — Das implizite Euler Verfahren (nach Leonhard Euler) oder auch Rückwärtsdifferenzenverfahren ist das einfachste implizite Verfahren zur numerischen Lösung eines Anfangswertproblems. Das Verfahren Zur numerischen Lösung des Anfangswertproblems: für … Deutsch Wikipedia
Heun-Verfahren — Das Heun Verfahren, benannt nach Karl Heun, ist ein einfaches Verfahren zur numerischen Lösung von Anfangswertaufgaben. Es ist ein Einschrittverfahren und gehört zu der Klasse der Runge Kutta Verfahren. Im Gegensatz zum Expliziten Euler Verfahren … Deutsch Wikipedia
Einschritt-Verfahren — In der numerischen Mathematik ist ein Einschrittverfahren eine Methode zur näherungsweisen Lösung von Anfangswertproblemen. Im Gegensatz zu Mehrschrittverfahren werden hier zur Berechnung der Näherung an die Lösung im nächsten Zeitpunkt… … Deutsch Wikipedia
Euler-Gleichung — Die Euler Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das… … Deutsch Wikipedia
Euler-Gleichungen — Die Euler Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das… … Deutsch Wikipedia
Runge-Kutta-Verfahren — Einige Runge Kutta Verfahren im Vergleich. Die s stufigen Runge Kutta Verfahren (nach Carl Runge und Martin Wilhelm Kutta) sind Einschrittverfahren zur näherungsweisen Lösung von Anfangswertproblemen in der numerischen Mathematik. Wenn von dem… … Deutsch Wikipedia
Halbschrittverfahren — Das Heun Verfahren, benannt nach Karl Heun, ist ein einfaches Verfahren zur numerischen Lösung von Anfangswertaufgaben. Es ist ein Einschrittverfahren und gehört zu der Klasse der Runge Kutta Verfahren. Im Gegensatz zum Expliziten Euler Verfahren … Deutsch Wikipedia