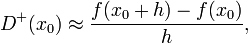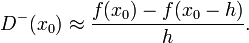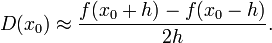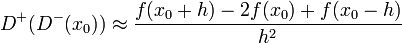Finite-Differenzen

Die Finite-Differenzen-Methode ist das einfachste numerische Verfahren zur Lösung gewöhnlicher und partieller Differentialgleichungen.

Zunächst wird das Gebiet, für das die Gleichung gelten soll, in eine endliche (finite) Zahl von Gitterpunkten eines Gitters von senkrecht aufeinander stehenden Linien eingeteilt. Den Gitterpunkten entsprechen dann die Kreuzungspunkte. Die Ableitungen an den Gitterpunkten werden dann durch Differenzen approximiert (siehe dazu Numerische Differentiation). Die partiellen Differentialgleichungen werden so in ein System von Differenzengleichungen umformuliert und mittels verschiedener Algorithmen entweder implizit oder explizit gelöst.

Verfahren dieser Art finden verbreitete Anwendung bei fluiddynamischen Simulationen, zum Beispiel in der Meteorologie und der Astrophysik.

Differenzenquotient

Ein naheliegender Ansatz ist die Verwendung des Vorwärtsdifferenzenquotienten

$D^+(x_0)\approx \frac{f(x_0+h)-f(x_0)}{h},$

bzw. des Rückwärtsdifferenzenquotienten

$D^-(x_0)\approx \frac{f(x_0)-f(x_0-h)}{h}.$

Dabei ist jedoch die Näherung im Vergleich zur Auslöschung relativ schlecht. Eine bessere Näherung erhält man durch Verwendung des zentralen Differenzenquotienten

$D(x_0)\approx \frac{f(x_0+h)-f(x_0-h)}{2h}.$

Beispiel

Wir diskretisieren die lineare Differenzialgleichung f''(x) = 2 in Ω = [0;1] mit der Randbedingung f(0) = f(1) = 3 auf einem Gitter mit der Maschenweite 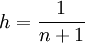$h = \frac{1}{n+1}$. Zur Diskretisierung der zweiten Ableitung nehmen wir den zentralen Differenzenquotienten der zweiten Ableitung

$D^+(D^-(x_0)) \approx \frac{f(x_0 + h) - 2f(x_0) + f(x_0 - h)}{h^2}$

Unser Gebiet Ω wird also im Inneren durch (n-1) Knoten diskretisiert. Wir nummerieren diese Knoten von x₁ bis x_{n − 1} durch. Für jeden dieser Knoten müssen wir die zweite Ableitung berechnen. Wir erhalten also (n-1) Gleichungen mit (n-1) Unbekannten.

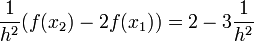$\frac{1}{h^2}( f(x_{2}) - 2f(x_1) ) = 2 - 3\frac{1}{h^2}$ und

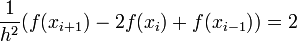$\frac{1}{h^2}(f(x_{i+1}) - 2f(x_i) + f(x_{i-1})) = 2$ für i = {2,..n − 2} und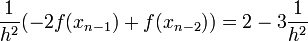

$\frac{1}{h^2}( - 2f(x_{n-1}) + f(x_{n-2})) = 2 - 3\frac{1}{h^2}$

Daraus erhalten wir ein Gleichungssystem Ax = b mit einer dünnbesetzten Matrix A. Solche Gleichungssysteme lassen sich effizient mit iterativen Lösern berechnen.

Weblinks

• Finite Differenzen Methode (Skript TU Berlin, pdf)