Modifizierte Wellenzahl

Die modifizierte Wellenzahl dient in der Physik der Bewertung einer Diskretisierung für eine Welle. Anhand der modifizierten Wellenzahl können wichtige numerische Eigenschaften eines Verfahrens, wie Dispersion, numerische Dämpfung oder die Aliasing-Grenze bestimmt werden. Sie ist auch wichtig zur Bestimmung des Zeitschrittlimits bei der expliziten numerischen Integration zeitabhängiger Probleme. Damit stellt der Verlauf der modifizierten Wellenzahl ein weitreichenderes Bewertungsmaß als eine reine Ordnungsanalyse dar. Diese Art der Betrachtung wird z. B. bei der Verfahrensentwicklung für die Direkte Numerische Simulation verwendet.

Grundlagen

Zur Bewertung eines numerischen Verfahrens bietet sich eine Analyse auf Wellenbasis an. Zum einen ist eine Welle eine Fundamentallösung nahezu aller partieller Differentialgleichungen, zum anderen liefert die Wellenlänge ein Maß für die Normierung der Schrittweite. Somit lässt sich die Qualität des Verfahrens in Abhängigkeit von den Punkten pro Wellenlänge angegeben. Die einfachste mathematische Form einer Welle lautet

$u = e^{i\left(kx\right)}$

mit der imaginären Einheit $i=\sqrt{-1}$ der Wellenzahl k. Die erste und zweite analytische Ableitung ergeben sich zu:

$\left.\frac{\partial u}{\partial x}\right|_\mathrm{exakt} = i k\cdot u, \quad\left.\frac{\partial^2 u}{\partial x^2}\right|_\mathrm{exakt}=-k^2\cdot u$.

Führt man die mit der Schrittweite Δx normierte Wellenzahl

$k^* = k\cdot\Delta x$

ein und löst die Gleichungen nach der dimensionslosen Wellenzahl bzw. ihrem Quadrat auf, so erhält man

$k^* = -i\cdot\Delta x\cdot\frac{\left.\partial u/\partial x\right|_\mathrm{exakt}}{u}, \quad k^{*2}=-\Delta x^2\cdot\frac{\left.\partial^2 u/\partial x^2\right|_\mathrm{exakt}}{u}$.

Die modifizierte Wellenzahl ergibt sich nun daraus, dass an Stelle der exakten Ableitungen die numerisch bestimmten Ableitungen in obige Gleichungen eingesetzt werden:

$k^*_\mathrm{mod} = -i\cdot\Delta x\cdot\frac{\left.\partial u/\partial x\right|_\mathrm{num.}}{u},\quad k^{*2}_\mathrm{mod}=-\Delta x^2\cdot\frac{\left.\partial^2 u/\partial x^2\right|_\mathrm{num.}}{u}$

Bei höheren Ableitungen erfolgt die Vorgehensweise entsprechend.

Dimensionslose Wellenzahl

Der Bereich der dimensionslosen Wellenzahl k ^* beschränkt sich auf den Wertebereich 0 bis π. Dies entspricht einer beliebig feinen Auflösung für k ^* = 0 beziehungsweise zwei Punkten pro Wellenlänge für k ^* = π, was der minimal erforderlichen Abstastrate gemäß der Nyquist-Frequenz entspricht. Die Anzahl der Punkte pro Wellenlänge ist gleich 2π / k ^* . Zur besseren Verdeutlichung ist dieser Zusammenhang in der folgenden Tabelle dargestellt.

k*mod	0	π/8	π/4	π/2	3/4 π	π
Punkte / Wellenlänge	∞	16	8	4	2,66	2

Real- und Imaginärteil der modifizierten Wellenzahl

Die modifizierte Wellenzahl ist in der Regel ein komplexe Größe, d.h. es kann neben dem Realteil k^*_mod,r auch ein Imaginärteil k^*_mod,i existieren. Dabei ist der Realteil die Amplitude der berechneten Ableitung einer Welle und der Imaginärteil entspricht dem Phasenversatz zur exakten Ableitung. Da bei einer zentralen Diskretisierung keine Vorzugsrichtung vorhanden ist, existiert kein Phasenversatz und somit ist der Imaginärteil der modifizierten Wellenzahl gleich null. Für höhere Ableitungen gilt dies entsprechend für das Quadrat k^*2_mod,r und höhere Potenzen der modifizierten Wellenzahl. Der Einfluss von Amplituden- und Phasenfehler der numerisch berechneten Ableitungen wird in den Abschnitten Erste Ableitung und Zweite Ableitung erörtert.

Beispiel

Um die Herleitung der modifizierten Wellenzahl anschaulich zu erläutern, wird beispielhaft die mit einer zentralen Finiten-Differenz zweiter Ordnung berechnete erste Ableitung betrachtet:

$\left.\frac{\partial u}{\partial x}\right|_\mathrm{num} = \frac{-u_{j-1}+u_{j+1}}{2\Delta x} = \frac{-e^{-i\cdot k\cdot\Delta x} + e^{i\cdot k\cdot\Delta x}}{2\Delta x} = \frac{-e^{-i\cdot k^*}+e^{i\cdot k^*}}{2\Delta x}$

$k^{*}_\mathrm{mod} = -i\cdot\Delta x\cdot\frac{-e^{-i\cdot k^*}+e^{i\cdot k^*}}{2\Delta x} = -i\cdot\frac{-\cos(-k^*)-i\cdot \sin(-k^*) + \cos(k^*)+i\cdot \sin(k^*)}{2}$

$k^{*}_\mathrm{mod} = -i\cdot\frac{-\cos(k^*)+i\cdot \sin(k^*) + \cos(k^*)+i\cdot \sin(k^*)}{2}$

Damit ergibt sich die modifizierte Wellenzahl zu

$k^{*}_\mathrm{mod} = \sin(k^*)$.

Da es sich um eine zentrale Differenz handelt, weist die modifizierte Wellenzahl nur einen Real- und keinen Imaginärteil auf.

Erste Ableitung

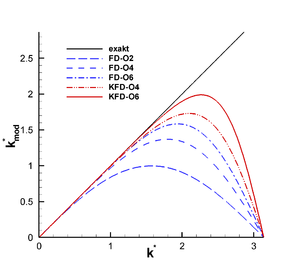
Das linke Diagramm zeigt die modifizierte Wellenzahl k^*_mod für verschiedene explizite und kompakte Finite Differenzen im Vergleich zur exakten Lösung k ^* . Da es sich hierbei um zentrale Diskretisierungen handelt, ist der Imaginärteil k^*_mod,i gleich null und es existiert nur ein Realteil von k^*_mod. Deutlich ist zu erkennen, dass für eine höhere Ordnung als auch bei Verwendung eines kompaktes Diskretisierungsschemas (rote Linien) die modifizierte Wellenzahl für größere Wellenzahlen k^*, d. h. für eine geringere Auflösung der exakten Lösung folgt.

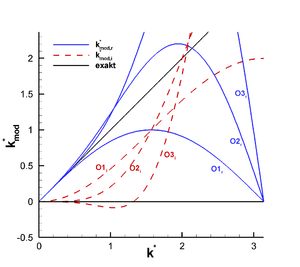
Die Eigenschaften von verschiedenen einseitigen Finiten-Differenzen ist in der rechten Abbildung dargestellt. Der Realteil der modifizierten Wellenzahl ist für erste, zweite und dritte Ordnung durch die blauen Linien gegeben. Zwar erreicht man durch eine höhere Ordnung eine bessere Übereinstimmung im Bereich kleiner dimensionsloser Wellenzahlen, jedoch ergeben sich im Bereich schlechterer Auflösungen (k^*>1,2) deutlich zu hohe Werte für die modifizierte Wellenzahl (siehe hierzu auch Abschnitt Zusammenhang mit dem Zeitschrittlimit). Für nach rechts gerichtete Differenzen ist der Imaginärteil der modifizierten Wellenzahl durch die gestrichelten roten Linien gegeben.

Modifizierte Wellenzahl für verschiedene zentrale Finite-Differenzen von zweiter bis sechster Ordnung.

Modifizierte Wellenzahl für einseitige nach der rechten Seite gewichteten Finite-Differenzen.

Anfachung und Dämpfung

Für die einfache Advektionsgleichung

$\frac{\partial u}{\partial t} + c\cdot\frac{\partial u}{\partial x} = 0$

mit positiver Advektionsgeschwindigkeit c entspricht ein positiver Wert von k^*_mod,i einer Anfachung. Aufgrund der Gewichtung des Differenzensterns in Stromabrichtung spricht man deshalb auch von einem Downwind-Verfahren. Im Fall eines Upwind-Verfahrens ändert sich lediglich das Vorzeichen des Imaginärteils. Damit erhält man einen nahezu durchgehend negativen Imaginärteil, der dämpfend wirkt und somit in der Lage ist, ein numerisches Verfahren zu stabilisieren.

Dispersion und Aliasing

Für ein Transportgleichung ergibt ein Amplitudenfehler, d. h. eine Abweichung von k^*_mod,r von der exakten Lösung k^*, einen Fehler in der Ausbreitungsgeschwindigkeit einer Welle, was als Dispersion bezeichnet wird. Aus der Advektionsgleichung lässt sich ableiten, dass die Phasengeschwindigkeit c_ph proportional zum Verhältnis der modifizierten Wellenzahl k^*_mod,r und der dimensionslosen Wellenzahl k^* ist. Die Gruppengeschwindigkeit c_gr verhält sich wie die Ableitung der modifizierten Wellenzahl:

• Phasengeschwindigkeit: $c_\mathrm{ph}\sim\frac{k^*_{\mathrm{mod},r}}{k^*}$
• Gruppengeschwindigkeit: $c_\mathrm{gr}\sim\frac{\partial k^*_{\mathrm{mod},r}}{\partial k^*}$

Da der Realteil der modifizierten Wellenzahl für die minimale Auflösung von zwei Punkten pro Wellenlänge zu null geht, ergeben sich ab dem Maximum von k^*_mod,r Phasengeschwindigkeiten, die man bereits für feinere Auflösungen erhält. Die Aliasinggrenze ist somit das Maximum der modifizierten Wellenzahl. Dort erhält man eine Gruppengeschwindigkeit von null und für größere Werte von k^* ergibt sich eine negative Gruppengeschwindigkeit, d.h. Störungen breiten sich entgegen der physikalischen Ausbreitungsrichtung, welche durch die zu lösende partielle Differentialgleichung gegeben ist, aus. Damit erklärt sich auch, weshalb eine Streckung ins Unendliche (z. B. bei Randbedingungen), die mathematisch durchaus formulierbar ist, nicht für instationäre Probleme geeignet ist.

Zweite Ableitung

Quadrate der modifizierten Wellenzahl für die zweite Ableitung, berechnet mit zentrale Finite-Differenzen von zweiter bis sechster Ordnung.

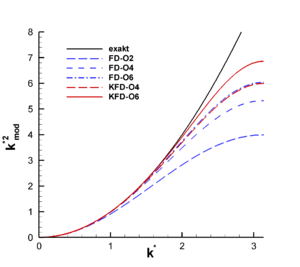
Das nebenstehende Diagramm zeigt das Quadrat der modifizierten Wellenzahl für verschiedene explizite und kompakte Finite-Differenzen. Da es sich um zentrale Diskretisierungssterne handelt, weist dieses nur einen Realteil auf. Man erkennt, dass mit höherer Ordnung und mit einer kompakten Diskretisierung eine bessere Übereinstimmung mit der exakten Lösung k^*2 ergibt. Außerdem erhält man mit wachsender Qualität der Diskretisierung einen höheren Wert für die mit nur zwei Punkten aufgelöste Welle. Somit werden schlecht aufgelöste Wellen aufgrund der viskosen Terme besser gedämpft, was vor allem bei nichtlinearen Rechnungen von Bedeutung ist.

Der Realteil k^*2_mod,r entspricht der Dämpfung für die einfache Diffusionsgelichung

$\frac{\partial u}{\partial t} = d\cdot\frac{\partial^2 u}{\partial x^2}$.

Im allgemeinen werden viskose Terme, d. h. 2. Ableitung nicht mit einer schiefen Diskretisierung berechnet, da der damit verbundene Imaginärteil k^*2_mod,i eine künstliche Advektion hervorruft.

Zusammenhang mit der Konsistenzordnung

Bei der Konsistenzordnung wird das Verhalten des Abbruchfehlers bei einer Verkleinerung der Schrittweite betrachtet. So führt beispielsweise eine Halbierung der Schrittweite bei einer Diskretisierung 2. Ordnung zu einer Verringerung des Fehlers um den Faktor 4. Da die Konsistenzordnung auf einer Taylorreihe beruht, gilt dies natürlich nur für kleine Schrittweiten, d.h. für bereits gut aufgelöste Probleme. Dies ist der Fall für k^* → 0. Die Ordnung liefert somit keine Aussagen über das Verhalten des numerischen Verfahrens für schlechter aufgelöste Probleme. Zwar ergibt sich bei höherer Ordnung eine bessere Übereinstimmung der Ableitungen $\partial^N k^*_{mod}/\partial k^{*N}$ für k^*=0 mit der exakten Lösung, jedoch lässt sich daraus nicht direkt die Konsistenzordnung ablesen.

Zusammenhang mit dem Zeitschrittlimit

Das Zeitschrittlimit für explizite Integrationsverfahren wird durch die maximal auftretenden Frequenzen beziehungsweise zeitlichen Anfachungs- und Dämpfungsraten bestimmt. Im Falle der Advektionsgleichung ist die größtmögliche Zeitableitung und damit die höchste Frequenz proportional zum Maximalwert der ersten Raumableitung. Damit ist der Maximalwert der modifizierten Wellenzahl k^*mod ein direktes Maß für das Zeitschrittlimit. Bei Disffusionsproblemen skaliert die größtmögliche Frequenz mit dem Maximum des Quadrats der modifizierten Wellenzahl, so dass hier Werte von k^*2mod eine stärkere Beschränkung für den maximal möglichen Zeitschritt darstellen.

Siehe auch

• Finite-Differenzen-Methode
• Finite-Volumen-Verfahren
• Konsistenzordnung
• CFL-Zahl und DFL-Zahl

Literatur

• S. Lele: Compact finite differences with spectral-like resolution. Journal of Computational Physics, Vol. 103, 1992, S. 16–42, ISSN 0021-9991
• M. Kloker: A robust high-resolution split-type compact FD scheme for spatial DNS of boundary-layer transition. Applied Scientific Research, Vol. 59, 1998, S. 353–377, doi:10.1023/A:1001122829539

Weblinks

• Diagrammkatalog zum Lösungsverhalten von Finiten-Differenzen, Vorlesungsmaterial Universität Stuttgart (PDF-Datei; 2,29 MB)