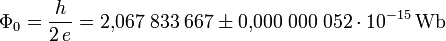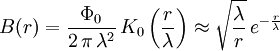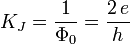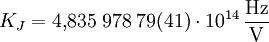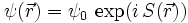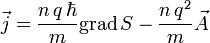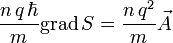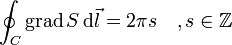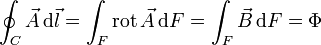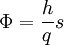Fluxon

Als Flussquantisierung bezeichnet man den Effekt, dass der magnetische Fluss durch einen Ring aus supraleitendem Material nur ganzzahlige Vielfache des Flussquants betragen kann. ^[1] Die Flussquantisierung ist eine Folge des Meißner-Ochsenfeld-Effektes. Statt Flussquant sind auch die Bezeichnungen Fluxon und Fluxoid gebräuchlich.

Der Begriff Fluxon wird auch in der Diskretisierung der Magnetohydrodynamik mittels Finite-Elemente-Methode verwendet.

Flussquant im Supraleiter

Die Quantisierung des magnetischen Flusses kann man durch die quantenmechanische Betrachtung des im Supraleiter verteilten Stromflusses feststellen:

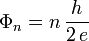$\Phi_n = n\,\frac{h}{2\,e}$ mit $n \in \mathbb{N}$

Das Flussquant weist einen Betrag des magnetischen Flusses von

$\Phi_0=\frac{h}{2\,e} = 2{,}067\;833\;667\pm 0{,}000\;000\;052\cdot 10^{-15}\,\mathrm{Wb}$ ^[2]

auf. Hierbei ist h das plancksche Wirkungsquantum und e die Elementarladung.

Der Faktor 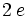$2\,e$ im Nenner der Formel bezeichnen eine doppelte Elektronenladung. Auf diese doppelte Elektronenladung stützt sich das BCS-Modell, welches die sogenannten Cooper-Paare als Ursache der Supraleitung ansieht.

Die Verteilung des magnetischen Feldes 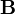$\mathbf{B}$ eines einzelnen Flussschlauchs im Raum wird durch die Gleichung

$B(r) = \frac{\Phi_0}{2\,\pi\,\lambda^2}\,K_0\left(\frac{r}{\lambda}\right) \approx\sqrt{\frac{\lambda}{r}}\,e^{-\frac{r}{\lambda}}$

beschrieben, wobei K₀(z) die Bessel-Funktion darstellt.

Abrikossow-Turbulenz

Ein Flussquant im Sinne der Abrikossow-Turbulenz ist ein nadelförmiger Einkristall (Kern) in einem Supraleiter 2. Art, der von Supraströmen umgeben ist.

Das magnetische Feld durch solch einen Einkristall und dessen Nachbarschaft hat eine Größenordnung von etwa 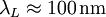$\lambda_L \approx 100\,\mathrm{nm}$ und ist durch die Phaseneigenschaften des magnetischen Vektorpotentials in der Quantenelektrodynamik quantisiert.

Josephson-Turbulenz

Die Josephson-Turbulenz ist das Gegenstück zur Abrikossow-Turbulenz in kreisenden Supraströmen ohne physikalischen Kern in einem Supraleiter 2. Art. Der Kern ist in diesem Fall der mathematische Mittelpunkt des Kreises.

Das Inverse des Flussquants ist hierbei die Josephson-Konstante:

$K_J = \frac{1}{\Phi_0} = \frac{2\,e}{h}$

Ihr Wert kann sehr genau gemessen werden und beträgt nach CODATA 2002

$K_J=4{,}835\;978\;79(41)\cdot 10^{14}\,\frac{\mathrm{Hz}}{\mathrm{V}}$

Herleitung der Flussquantisierung

Der supraleitende Zustand ist ein quantenmechanischer Zustand, der sich über makroskopische Längenskalen erstreckt. Er kann daher durch eine makroskopische Wellenfunktion beschrieben werden:

$\psi(\vec{r})=\psi_0\,\exp(i\,S(\vec{r}))$

Dabei wird (in quasiklassischer, als makroskopischer Näherung) davon ausgegangen, dass ψ eine konstante Amplitude ψ₀ hat und nur die Phase S ortsabhängig ist. Für diese Wellenfunktion gilt die London-Gleichung

$\vec{j}=\frac{n\,q\,\hbar}{m} \text{grad}\, S-\frac{n\,q^2}{m}\vec{A}$

Infolge des Meißner-Ochsenfeld-Effekts verschwindet die magnetische Induktion 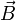$\vec{B}$ im Inneren eines Supraleiters. Für den statischen Fall gilt 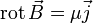$\mbox{rot} \,\vec{B}= \mu \vec{j}$ (eine der Maxwellgleichungen) womit auch 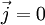$\vec{j}=0$ für das Innere des Supraleiters folgt. Es gilt demzufolge

$\frac{n\,q\,\hbar}{m} \text{grad}\, S=\frac{n\,q^2}{m}\vec{A}$

Fasst man die Konstanten zusammen und integriert beide Seiten entlang eines geschlossenen Weges C durch das Innere des Supraleiters, so erhält man

$\oint_C \text{grad}\, S \,\text{d}\vec{l}=\frac{q}{\hbar} \oint_C \vec{A} \,\text{d}\vec{l}$

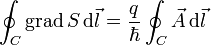
Die linke Seite beschreibt die Änderung der Phase S beim Durchlaufen des geschlossenen Weges C. Da die Wellenfunktion eindeutig ist, kann die Phasenänderung nur ganzzahlige Vielfache von 2 π betragen. Es gilt also

$\oint_C \text{grad}\, S \,\text{d}\vec{l}=2\pi s \quad,s\in\mathbb{Z}$

Nach dem Satz von Stokes gilt

$\oint_C \vec{A} \,\text{d}\vec{l}=\int_F \text{rot} \,\vec{A} \,\text{d} F=\int_F \vec{B} \,\text{d} F=\Phi$

wobei F eine durch C begrenzte Fläche ist und Φ der magnetische Fluss durch diese Fläche. Es ergibt sich insgesamt

$\Phi=\frac{h}{q}s$

Der Fluss durch einen supraleitenden Ring ist also quantisiert. Experimentell ergibt sich q = − 2e, was darauf hindeutet, dass die Elektronen Paare, die sogenannten Cooper-Paare bilden.

^[3]

Fluxon in der Magnetohydrodynamik

In der Magnetohydrodynamik (MHD) bezeichnet man mit Fluxon eine diskretisierte magnetische Feldlinie endlichen Betrags in einem Finite-Elemente-Modell. Hierbei wird versucht die Topologie des untersuchten Sachverhalts unter der Berücksichtigung begrenzter Rechenkapazitäten möglichst zu erhalten.

Siehe auch

• Fluxtronik
• Physikalische Konstanten
• Josephson-Effekt
• Flussschlauch

Einzelnachweise

1. ↑ Ch. Kittel Einführung in die Festkörperphysik Oldenburg ISBN 978-3-486-57723-5 Seite 306 Zitat: „Wir zeigen nun, dass der gesammte magnetische Fluss durch einen supraleitenden Ring nur quantisierte Werte annehmen kann, und zwar nur ganzzahlige Vielfache des Flussquants“
2. ↑ Wert nach CODATA 2006 siehe [1] (abgerufen am 9. Oktober 2007)
3. ↑ Rechnung nach Ch. Kittel Einführung in die Festkörperphysik Oldenburg ISBN 978-3-486-57723-5 Seiten 299-300, 306-308