- Bessel-Funktion
-
Die Besselsche Differentialgleichung
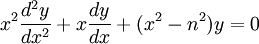 .
.
ist eine lineare gewöhnliche Differentialgleichung zweiter Ordnung. Dabei ist n meistens eine ganze Zahl.
Sie ist benannt nach Friedrich Wilhelm Bessel.
Inhaltsverzeichnis
Bessel-Funktionen
Allgemein
Die Lösungen der Besselschen Differentialgleichung heißen Bessel-Funktionen. Sie spielen eine wichtige Rolle in der Physik, da die Besselsche Differentialgleichung den radialen Anteil der Laplace-Gleichung bei zylindrischer Symmetrie darstellt. Auf die Bessel-Funktionen trifft man unter anderem bei der Untersuchung von Eigenschwingungen einer kreisförmigen Membran oder Orgelpfeife, der Ausbreitung von Wasserwellen in runden Behältern, der Wärmeleitung in Stäben, der Analyse des Frequenzspektrums von frequenzmodulierten Signalen, der Feldverteilung im Querschnitt von Rundhohlleitern, den stationären Zuständen von Kastenpotentialen und der Intensität von Lichtbeugung an kreisförmigen Löchern. Man zählt die Bessel-Funktionen wegen ihrer vielfältigen Anwendungen in der mathematischen Physik zu den speziellen Funktionen.
Die Besselsche Differentialgleichung besitzt zwei linear unabhängige Lösungen. Für nicht-ganzzahlige n sind Jn und J − n linear unabhängige Lösungen. Für ganzzahlige n ist neben der Bessel-Funktion erster Gattung Jn (auch einfach Bessel-Funktion genannt) die Bessel-Funktion zweiter Gattung Yn (auch Weber-Funktion oder Neumann-Funktion genannt) die zweite, linear unabhängige Lösung.
Die Darstellungen der Bessel-Funktionen lauten
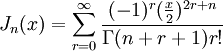 , wobei Γ(x) die Gammafunktion ist, sowie
, wobei Γ(x) die Gammafunktion ist, sowie
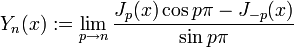 .
.
Die Bessel-Funktion 2. Gattung hat im Ursprung eine logarithmische Singularität, weshalb sie sich nicht durch eine Potenzreihe darstellen lässt. Durch Ausführung des Grenzüberganges mit der Regel von L’Hospital ergibt sich:
Hierbei ist γ die Eulersche Konstante und Hn die harmonische Reihe.
Weitere Eigenschaften
- Für die Bessel-Funktionen gelten die Rekursionsbeziehungen:
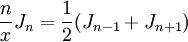 ,
,
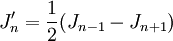 .
.
- Diese Beziehungen gelten auch für die Bessel-Funktion 2. Gattung.
- Für ganzzahlige n gilt weiterhin:
- Verbindung zur hypergeometrischen Funktion:
- Die Bessel-Funktion kann in Abhängigkeit zur hypergeometrischen Funktion ausgedrückt werden.
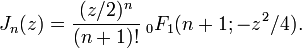
- Dieser Ausdruck hängt mit der Entwicklung der Bessel-Funktion in Abhängigkeit zur Bessel-Clifford-Funktion zusammen.
- Für alle
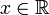 gilt
gilt 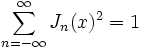 .
.
- Für alle
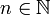 gilt
gilt 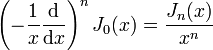 .
.
Modifizierte Bessel-Funktionen
Tritt eine Bessel-Funktion nur mit rein imaginären Zahlen auf, so spricht man von modifizierten Bessel-Funktionen.
ist die modifizierte Bessel-Funktion n-ter Ordnung. Sie löst die Differentialgleichung
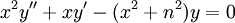 .
.
Eine zweite Lösung für diese Differentialgleichung ist
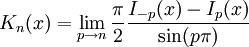 ,
,
die auch als MacDonald-Funktion bekannt ist.
Literatur
- Milton Abramowitz, Irene Stegun: Handbook of Mathematical Functions. Dover, New York 1972, S. 355.
- Paul Schafheitlin Die Theorie der Besselschen Funktionen. B. G. Teubner, Leipzig 1908.
- J. H. Graf, E. Gubler: Einleitung in die Theorie der Bessel'schen Funktionen. Erster Band Zweiter Band. K. J. Wyss, Bern 1900
- Carl Neumann: Theorie der Bessel'schen Functionen: ein Analogon zur Theorie der Kugelfunctionen. B. G. Teubner, Leipzig 1867.
Weblinks
Wikimedia Foundation.

_svg.png)
_svg.png)
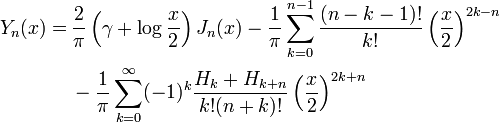
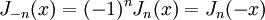
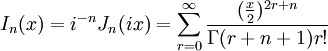
_svg.png)
_svg.png)