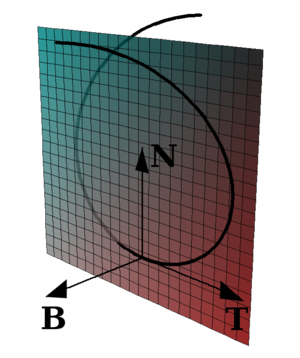
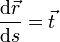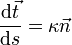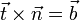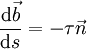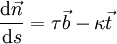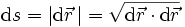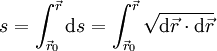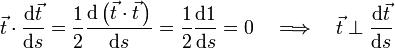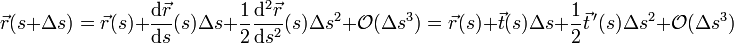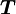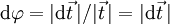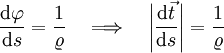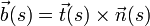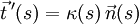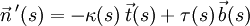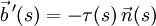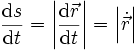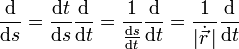- Frenetsches Dreibein
-
Die frenetschen Formeln (Frenet-Formeln), benannt nach dem französischen Mathematiker Jean Frédéric Frenet, sind die zentralen Gleichungen in der Theorie der Raumkurven, einem wichtigen Teilgebiet der Differentialgeometrie. Sie werden auch Frenet-Serret Formeln genannt nach Joseph Serret, der sie vollständig angab.
Die Formeln verwenden eine Orthonormalbasis aus drei Vektoren (Tangentenvektor
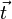 , Hauptnormalenvektor
, Hauptnormalenvektor 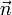 und Binormalenvektor
und Binormalenvektor 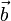 ), die das lokale Verhalten der Kurve
), die das lokale Verhalten der Kurve 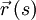 beschreiben, und drücken die Ableitungen dieser Vektoren nach der Bogenlänge s als Linearkombinationen der genannten drei Vektoren aus. Dabei treten die für die Kurve charakteristischen Skalare Krümmung κ und Torsion τ auf.
beschreiben, und drücken die Ableitungen dieser Vektoren nach der Bogenlänge s als Linearkombinationen der genannten drei Vektoren aus. Dabei treten die für die Kurve charakteristischen Skalare Krümmung κ und Torsion τ auf.Beschreibung
Der Vektor
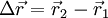 verbindet zwei Punkte der Bahn und hat die Länge
verbindet zwei Punkte der Bahn und hat die Länge 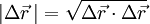 . Für
. Für 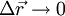 geht
geht 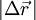 gegen die Bogenlänge des zwischen
gegen die Bogenlänge des zwischen 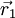 und
und 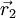 gelegenen Bahnstücks:
gelegenen Bahnstücks:Vom Anfangspunkt
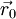 zum Punkt
zum Punkt 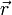 beträgt die Bogenlänge der Bahn
beträgt die Bogenlänge der BahnGegeben sei eine durch die Bogenlänge s parametrisierte Raumkurve:
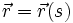 .
.
Für einen Kurvenpunkt
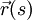 erhält man durch Ableiten nach s den Tangenteneinheitsvektor, der die momentane Richtung der Kurve, also die Änderung der Position bei einer Änderung der Bogenlänge, angibt:
erhält man durch Ableiten nach s den Tangenteneinheitsvektor, der die momentane Richtung der Kurve, also die Änderung der Position bei einer Änderung der Bogenlänge, angibt: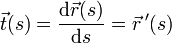 .
.
Wegen
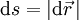 ist der Betrag der Ableitung gleich 1; somit handelt es sich um einen Einheitsvektor. Der Tangenteneinheitsvektor ändert entlang der Bahn im Allgemeinen seine Richtung, nicht aber seine Länge (er bleibt stets ein Einheitsvektor)
ist der Betrag der Ableitung gleich 1; somit handelt es sich um einen Einheitsvektor. Der Tangenteneinheitsvektor ändert entlang der Bahn im Allgemeinen seine Richtung, nicht aber seine Länge (er bleibt stets ein Einheitsvektor) 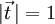 bzw.
bzw. 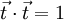 . Daraus kann man folgern, dass die Ableitung des Tangenteneinheitsvektors senkrecht zu diesem steht:
. Daraus kann man folgern, dass die Ableitung des Tangenteneinheitsvektors senkrecht zu diesem steht:Die Bahnkurve kann man in eine Taylorreihe um s entwickeln:
Die Näherungskurve zweiter Ordnung in Δs ist eine Parabel, die in der von
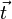 und
und 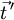 aufgespannten Schmiegeebene liegt.
aufgespannten Schmiegeebene liegt.Um den Betrag von
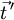 zu berechnen, betrachtet man den Schmiegkreis, der sich am betrachteten Bahnpunkt an dessen Näherungsparabel anschmiegt, d.h. den Kreis, der durch den gegebenen Kurvenpunkt geht, dort die gleiche Richtung hat wie die Kurve und auch in der zweiten Ableitung mit der Kurve übereinstimmt. Der Winkel zwischen Tangentenvektoren benachbarter Kurvenpunkte (
zu berechnen, betrachtet man den Schmiegkreis, der sich am betrachteten Bahnpunkt an dessen Näherungsparabel anschmiegt, d.h. den Kreis, der durch den gegebenen Kurvenpunkt geht, dort die gleiche Richtung hat wie die Kurve und auch in der zweiten Ableitung mit der Kurve übereinstimmt. Der Winkel zwischen Tangentenvektoren benachbarter Kurvenpunkte (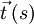 und
und 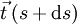 ) sei
) sei 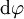 . Damit gilt
. Damit giltDa der Tangenteneinheitsvektor senkrecht auf dem Radiusvektor des Schmiegkreises steht, ist der Winkel zwischen benachbarten Radiusvektoren (
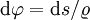 ) identisch mit dem Winkel zwischen den Tangentenvektoren benachbarter Kurvenpunkte (
) identisch mit dem Winkel zwischen den Tangentenvektoren benachbarter Kurvenpunkte (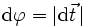 ). Daraus folgt mit
). Daraus folgt mit 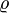 als Schmiegkreisradius (= Krümmungsradius):
als Schmiegkreisradius (= Krümmungsradius):Der reziproke Krümmungsradius
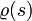 heißt Krümmung
heißt Krümmung 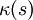 und gibt die Stärke der Richtungsänderung über die Bogenlänge, also den Betrag von
und gibt die Stärke der Richtungsänderung über die Bogenlänge, also den Betrag von 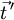 an:
an: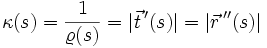 .
.
Normierung von
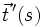 liefert den Hauptnormaleneinheitsvektor
liefert den Hauptnormaleneinheitsvektor 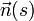 (Krümmungsvektor). Da der Tangenteneinheitsvektor tangential zum Schmiegkreis steht und der Hauptnormaleneinheitsvektor senkrecht dazu, gibt
(Krümmungsvektor). Da der Tangenteneinheitsvektor tangential zum Schmiegkreis steht und der Hauptnormaleneinheitsvektor senkrecht dazu, gibt 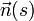 die Richtung der Verbindungsgeraden vom Kurvenpunkt zum Schmiegkreismittelpunkt (die Richtung, in die sich
die Richtung der Verbindungsgeraden vom Kurvenpunkt zum Schmiegkreismittelpunkt (die Richtung, in die sich 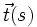 ändert) an.
ändert) an.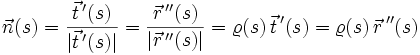 .
.
Der Normalenvektor der Schmiegeebene wird mit Hilfe des Vektorprodukts aus Tangenteneinheitsvektor und Hauptnormaleneinheitsvektor festgelegt und heißt Binormaleneinheitsvektor:
Tangenten-, Hauptnormalen- und Binormaleneinheitsvektor bilden eine Orthonormalbasis des
 , d. h. diese Vektoren haben alle den Betrag 1 und sind paarweise senkrecht zueinander. Man bezeichnet diese Orthonormalbasis auch als begleitendes Dreibein der Kurve. Die frenetschen Formeln drücken die Ableitungen der genannten Basisvektoren als Linearkombinationen dieser Basisvektoren aus:
, d. h. diese Vektoren haben alle den Betrag 1 und sind paarweise senkrecht zueinander. Man bezeichnet diese Orthonormalbasis auch als begleitendes Dreibein der Kurve. Die frenetschen Formeln drücken die Ableitungen der genannten Basisvektoren als Linearkombinationen dieser Basisvektoren aus:Dabei stehen
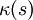 für die Krümmung und
für die Krümmung und 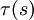 für die Windung (Torsion) der Kurve im betrachteten Kurvenpunkt.
für die Windung (Torsion) der Kurve im betrachteten Kurvenpunkt.Anhand des begleitenden Dreibeins lassen sich Krümmung und Torsion jeweils als Richtungsänderung eines bestimmten Tangenteneinheitsvektors veranschaulichen.
Der Torsion
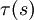 entspricht die Richtungsänderung des Binormaleneinheitsvektors:
entspricht die Richtungsänderung des Binormaleneinheitsvektors:- Je größer die Torsion, desto schneller ändert der Binormaleneinheitsvektor
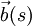 in Abhängigkeit von
in Abhängigkeit von  seine Richtung. Ist die Torsion überall 0, so handelt es sich bei der Raumkurve um eine ebene Kurve, d. h. es gibt eine gemeinsame Ebene, auf der alle Punkte der Kurve liegen.
seine Richtung. Ist die Torsion überall 0, so handelt es sich bei der Raumkurve um eine ebene Kurve, d. h. es gibt eine gemeinsame Ebene, auf der alle Punkte der Kurve liegen.
Der Krümmung
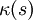 entspricht die Richtungsänderung des Tangenteneinheitsvektors:
entspricht die Richtungsänderung des Tangenteneinheitsvektors:- Je stärker die Krümmung
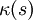 ist, desto schneller ändert der Tangenteneinheitsvektor
ist, desto schneller ändert der Tangenteneinheitsvektor 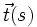 in Abhängigkeit von
in Abhängigkeit von  seine Richtung.
seine Richtung.
Punkte der Raumkurve mit der Krümmung 0, in denen kein Schmiegkreis existiert, in denen also die Ableitung des Tangenteneinheitsvektors der Nullvektor ist, heißen Wendepunkte und sind gesondert zu behandeln. Dort verlieren die Begriffe Normalenvektor und Binormalenvektor ihren Sinn. Haben alle Punkte die Krümmung 0, so ist die Raumkurve eine Gerade.
Frenetsche Formeln in Abhängigkeit von anderen Parametern
Die oben angegebenen Formeln sind in Abhängigkeit von der Bogenlänge s definiert. Oft sind aber die Raumkurven in Abhängigkeit von anderen Parametern, z. B. von der Zeit gegeben. Um die Beziehungen durch den neuen Parameter t auszudrücken, verwendet man folgende Relation:
somit kann man die Ableitungen von
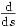 nach
nach 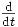 umschreiben:
umschreiben:Eine dreimal nach t differenzierbare Kurve
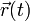 besitzt an jeder Parameterstelle mit
besitzt an jeder Parameterstelle mit 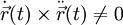 die folgenden charakteristischen Vektoren und Skalare:
die folgenden charakteristischen Vektoren und Skalare:Tangentenvektor 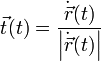
Binormalenvektor 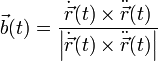
Hauptnormalenvektor 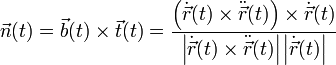
Krümmung 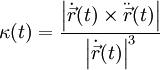
Torsion 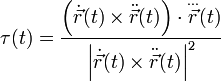
Wikimedia Foundation.