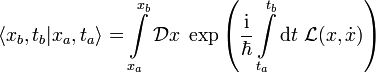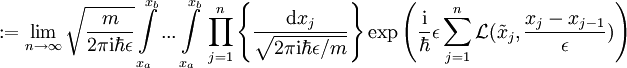- Funktionalintegral
-
Das Pfadintegral (oder Funktionalintegral) ist ein mathematisches Konstrukt, das in der physikalischen Feldtheorie verwendet wird.
Das Pfadintegral besteht aus im Grenzwert unendlich vielen, nacheinander auszuführenden ein- oder mehrdimensionalen Integralen; es ist unbedingt zu unterscheiden von dem Kurvenintegral der Funktionentheorie und Vektoranalysis. Die Verwechslungsgefahr rührt vor allem aus dem Englischen, in dem sowohl das Pfad- als auch das Kurvenintegral path integral genannt werden. Zur Unterscheidung wird das Pfadintegral im Englischen auch functional integral bzw. Feynman path integral genannt, nach seinem Erfinder Richard P. Feynman, basierend auf einer Produktformel von Paul A. M. Dirac zur Berechnung der Übergangswahrscheinlichkeit zwischen zwei Punkten A und B.
Die mathematische Präzisierung des Pfadintegrals fällt in die Funktionalanalysis. Für Pfade in Raumdimensionen größer als 1 ist das mathematisch saubere Fundament des Konvergenzverhaltens noch nicht vollständig gelegt und daher Gegenstand der Forschung.
Inhaltsverzeichnis
Pfadintegral in der Physik
Die so genannte Pfadintegralmethode wird insbesondere in der Quantenmechanik und in der Quantenfeldtheorie verwendet.
Formel
Die Amplitude für ein Teilchen in einer Dimension, das sich zum Zeitpunkt ta bei xa und zum Zeitpunkt tb bei xb befindet, ist gegeben durch
mit
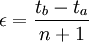 , wobei
, wobei 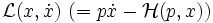 die Lagrangefunktion und
die Lagrangefunktion und 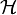 die Hamiltonfunktion ist, mit
die Hamiltonfunktion ist, mit 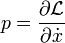 , und die durch die Punkte abgekürzten Integrationssymbole die n-dimensionale Integration explizit hervorheben. Alle n Integrale haben dieselbe obere und untere Integrationsgrenze, die Variablen
, und die durch die Punkte abgekürzten Integrationssymbole die n-dimensionale Integration explizit hervorheben. Alle n Integrale haben dieselbe obere und untere Integrationsgrenze, die Variablen 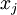 können als die zum Zeitpunkt
können als die zum Zeitpunkt 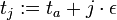 angenommenen Werte interpretiert werden und unterliegen keinerlei Einschränkung (die Beiträge zu
angenommenen Werte interpretiert werden und unterliegen keinerlei Einschränkung (die Beiträge zu 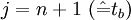 bzw.
bzw. 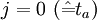 kann man für
kann man für 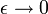 vernachlässigen). Wenn die Hamiltonfunktion explizit von der Zeit abhängt (z. B. im Wechselwirkungsbild) kann man das durch eine zusätzliche Abhängigkeit
vernachlässigen). Wenn die Hamiltonfunktion explizit von der Zeit abhängt (z. B. im Wechselwirkungsbild) kann man das durch eine zusätzliche Abhängigkeit 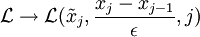 berücksichtigen.
berücksichtigen. 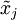 ist ein beliebiger Zwischenwert in dem zu j gehörigen Intervall, z. B. dessen Mittelpunkt,
ist ein beliebiger Zwischenwert in dem zu j gehörigen Intervall, z. B. dessen Mittelpunkt, 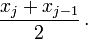
Beispiel
Im klassischen Fall bewegt sich ein freies Teilchen (ohne Potenzial) nur auf einer Geraden von einem Punkt A zu einem Punkt B. Der Weg, den es beschreibt, kann man mit dem Prinzip der kleinsten Wirkung berechnen, in diesem Fall trivialerweise eine Gerade. (Ein Beispiel für einen Fall mit Potenzial ist der eines Lichtstrahls, der Medien unterschiedlicher optischer Dichte passiert, hier ist der günstigste Weg (optischer Weg) keine Gerade mehr.) Umgekehrt kann man dem sich bewegenden Teilchen eine Wirkung zuordnen: Das zeitliche Integral der Differenz zwischen kinetischer und potentieller Energie (Lagrangefunktion) von Startzeitpunkt, an dem sich das Teilchen in A befindet, bis zum Endzeitpunkt, an dem sich das Teilchen in B befindet.
Mit einem Pfadintegral integriert man nun nicht nur über den klassischen Pfad, sondern über alle Pfade, das heißt, man betrachtet alle möglichen Pfade, auf denen das Teilchen von A nach B gelangen könnte und gewichtet den Pfad mit einem Phasenfaktor proportional zur Wirkung. Man nennt das auch Summe aller Pfade. Die Amplitude ist bei jedem Pfad gleich, aber die Phase, die von der jeweiligen Wirkung bestimmt wird, ist unterschiedlich. Somit trägt der klassische Pfad am meisten bei, da bei ihm die Wirkung am wenigsten variiert (Hamiltonsches Prinzip: der klassische Pfad eines Systems ist der, entlang dessen seine Lagrangefunktion extremal wird). Wenn die Wirkung variiert, hebt sich hingegen der größte Teil des Integrals weg. Bei Wirkungen, die groß gegen das Plancksche Wirkungsquantum sind, oszilliert der Integrand so schnell, dass sich alles weghebt (klassischer Grenzfall). In der Quantenmechanik jedoch sind die Wirkungen in der Größenordnung des Planckschen Wirkungsquantums, so dass auch Pfade neben dem klassischen einen Beitrag liefern.
Im Ganzen ist das Pfadintegral ein Ausdruck für einen Propagator, das heißt, wenn man ihn berechnet hat und die Wahrscheinlichkeitsamplitude einer Wellenfunktion zu einem Zeitpunkt und an einem Ort bekannt ist, dann kennt man mit dem Propagator (nach Integration über alle Anfangsorte) auch die Wahrscheinlichkeitsamplitude zu einem anderen Zeitpunkt.
Bücher
- Pfadintegrale in Quantenmechanik, Statistik und Polymerphysik", Spektrum Akademischer Verlag 1993 (vergriffen, online lesbar hier). Neuste englische Auflage: Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2006) (auch online verfügbar)
Wikimedia Foundation.