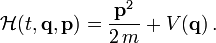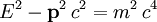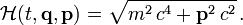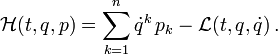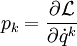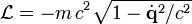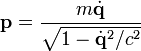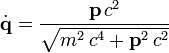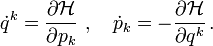Hamiltonfunktion

Die Hamilton-Funktion 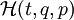$\mathcal H(t,q,p)$ (nach William Rowan Hamilton) eines Systems von Teilchen ist seine Energie als Funktion der Orte und Impulse der Teilchen. Sie hängt von der Zeit t, den generalisierten Koordinaten 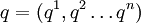$q=(q^1,q^2\dots q^n)$ und den generalisierten Impulsen 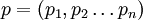$p=(p_1,p_2\dots p_n)$ ab. (Wir zählen die Ortskoordinaten, wie bei kontravarianten Größen üblich, mit oben stehenden Zahlen ab.)

Bei einem Teilchen der Masse m, das sich nichtrelativistisch in einem Potential V bewegt, setzt sie sich aus kinetischer und potentieller Energie zusammen

$\mathcal H(t,\mathbf q,\mathbf p)=\frac{\mathbf p^2}{2\,m}+V(\mathbf q)\,.$

Für ein relativistisches, freies Teilchen mit der Energie-Impuls-Beziehung

$E^2-\mathbf p^2\,c^2=m^2\,c^4$

ist die Hamilton-Funktion

$\mathcal H(t,\mathbf q,\mathbf p)=\sqrt{m^2\,c^4+ \mathbf p^2\,c^2}\,.$

Wenn die Hamiltonfunktion wie in diesen Beispielen nicht von der Zeit abhängt, behält das System von Teilchen seine anfängliche Energie, sie ist dann eine Erhaltungsgröße.

Die Hamiltonfunktion ist die Legendre-Transformierte der Lagrange-Funktion 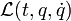$\mathcal L(t,q,\dot q)$, die von den generalisierten Koordinaten und ihren Geschwindigkeiten 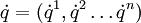$\dot q=(\dot q^1,\dot q^2\dots \dot q^n)$ abhängt,

$\mathcal H(t,q,p)= \sum_{k=1}^n \dot q^k\, p_k - \mathcal L(t, q,\dot q)\,.$

Dabei sind auf der rechten Seite mit den Geschwindigkeiten 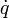$\dot q$ diejenigen Funktionen 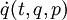$\dot q(t,q,p)$ gemeint, die man erhält, wenn man die Definition der Impulse

$p_k = \frac{\partial \mathcal L}{\partial \dot q^k}$

nach den Geschwindigkeiten auflöst.

Beispielsweise hängt beim freien relativistischen Teilchen mit der Lagrangefunktion

$\mathcal L= - m\,c^2 \sqrt{1-\dot \mathbf q^2/c^2}$

der Impuls gemäß

$\mathbf p=\frac{m \dot \mathbf q}{\sqrt{1-\dot \mathbf q^2/c^2}}$

von der Geschwindigkeit ab. Umgekehrt ist die Geschwindigkeit daher die Funktion

$\dot\mathbf q=\frac{\mathbf p\,c^2}{\sqrt{m^2\,c^4+\mathbf p^2\,c^2}}$

des Impulses.

Die Hamilton-Funktion bestimmt die zeitliche Entwicklung der Teilchenorte und Teilchenimpulse durch die Hamiltonschen Bewegungsgleichungen

$\dot q^k =\frac{\partial \mathcal H}{\partial p_k}\ ,\quad \dot p_k =-\frac{\partial \mathcal H}{\partial q^k} \,.$

Ebenso bestimmt der Hamiltonoperator die Zeitentwicklung in der Quantenmechanik. Man erhält ihn in vielen Fällen aus der Hamiltonfunktion durch sogenannte kanonische Quantisierung, indem man den algebraischen Ausdruck für 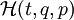$\mathcal H(t,q,p)$ als Funktion von Operatoren q und p liest, die den kanonischen Vertauschungsrelationen genügen.

siehe:Hamiltonsche Mechanik