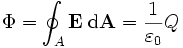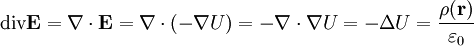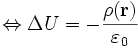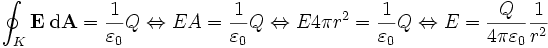Gausssches Gesetz

Das Gaußsche Gesetz beschreibt in der Elektrostatik den elektrischen Fluss durch eine geschlossene Fläche. Da das Gesetz in gleicher Weise auch für die klassische Gravitationstheorie formuliert werden kann, beschreibt es entsprechend den Fluss des gravitativen Beschleunigungsfeldes durch eine geschlossene Fläche.

Es handelt sich um eine Anwendung des Satzes von Gauß-Ostrogradski auf die Elektrostatik bzw. Elektrodynamik oder entsprechend die Gravitation. Es ist auch unter diesem Namen bekannt.

Wie das Ampèresche Gesetz, das Analogon für den Magnetismus, ist auch das Gaußsche Gesetz eine der vier maxwellschen Gleichungen (die erste) und somit fundamental für die klassische Elektrodynamik. Im Falle der Gravitation ergibt sich eine Gleichung, die der ersten Maxwellgleichung bis auf einige Konstanten äquivalent ist.

Formulierung

Vorbereitung der integralen Form

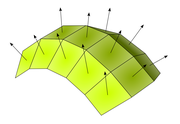
Der Satz benutzt den Begriff des Flusses, der für alle Vektorfelder definiert ist. Man denke sich einen mit der Ladung Q geladenen Körper, der von einer orientierten, geschlossenen Fläche A umgeben ist (orientiert bedeutet, dass es eine ausgezeichnete äußere und eine innere Seite gibt). Die Fläche kann dabei beliebig geformt sein, es kann eine Kugel sein oder ein irgendwie verbeulter Ballon. Von der Ladung fließen nun nach der Feldvorstellung die Feldlinien durch diese Oberfläche, die von Q ausgehen, genau wie Wasser durch die Oberfläche flösse, gäbe es innerhalb der Fläche eine Quelle oder Senke.

Weil das Universum nach heutigem Kenntnisstand elektrisch neutral ist, müssen alle Feldlinien, die von einer Ladung ausgehen, bei einer anderen, ungleichnamigen Ladung enden. Der Fluss einer Ladung außerhalb von A fließt auf der einen Seite herein, an einer anderen Stelle wieder heraus. Der Gesamtfluss hängt also nur von der eingeschlossenen Ladung Q ab. Der Kernpunkt des Gesetzes ist, dass er tatsächlich gleich Q geteilt durch eine Naturkonstante ist.

Die Oberfläche A kann in sehr kleine Vektoren 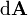$\mathrm d \mathbf A$ unterteilt werden, deren Betrag genau der Flächeninhalt des Stückes ist, und deren Richtung genau senkrecht auf der Ebene steht (Normalenvektor). Der Fluss durch ein solches Stück ist die Komponente des Vektorfeldes in der Richtung des Stückes mal dem Flächeninhalt; genau das wird durch das Skalarprodukt ausgedrückt. Der Gesamtfluss durch A ist dann das Oberflächenintegral dieses Produktes über die gesamte Oberfläche.

Mit dieser Vorbereitung ist die integrale Formulierung nun zugänglich:

Formulierung der integralen Form

Zur Veranschaulichung des Normalenvektors

Die integrale Form des Gesetzes lautet

$\Phi = \oint_A \mathbf E \; \mathrm d \mathbf A = { 1 \over \varepsilon_0 } Q$

mit dem Fluss Φ, dem Vektorfeld E und der eingeschlossen Ladung Q. 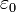$\varepsilon_0$ ist die Dielektrizitätskonstante des Vakuums.

Um den Summationsvorgang über die gesamte geschlossene Oberfläche auszuführen, denkt man sich folgende Schritte:

1. Die gesamte geschlossene Oberfläche sei aus sehr vielen winzigen, ebenen Flächenelementen zusammengesetzt.
2. Deren Orientierung im Raum wird durch jeweils einen Normalenvektor dA dargestellt, der senkrecht auf dem Flächenelement steht. Das sind die im Bild eingezeichneten Vektorpfeile.
3. Die Länge der Pfeile ist ein Maß für den Flächeninhalt eines Elementes.
4. Für jedes Flächenelement wird die lokale Feldstärke bestimmt. Das Ergebnis ist ein anderer Vektor E, der mit dem zugehörigen Normalenvektor einen beliebigen Winkel einschließen kann.
5. Für jedes Flächenelement wird das Skalarprodukt dA·E berechnet; das Ergebnis ist eine Zahl.
6. Die Ergebnisse aller Flächenelemente werden summiert und ergeben den Gesamtfluss Φ.
7. Das Ergebnis wird genauer, wenn man die Flächenelemente immer kleiner wählt (Grenzübergang).

Bei manchen Problemen wie der Berechnung elektrostatischer Felder in der Umgebung einfacher geometrischer Körper wie Platte, Linienladung oder Kugel kann man Φ durch geschickte Wahl der Flächenelemente auch ohne Integral berechnen.

Vorbereitung der differentiellen Form

Statt der makroskopischen Gesamtladung Q kann man die Ladung auch durch die Ladungsdichte ρ in jedem Punkt ausdrücken, wobei Q wiederum das Volumenintegral von ρ über dem gesamten von A eingeschlossenen Volumen V ist.

Die Divergenz ist gewissermaßen der Fluss durch eine beliebig kleine Oberfläche (für die mathematisch korrektere Erklärung sei auf den Artikel zur Divergenz verwiesen). Man erhält dann unter Verwendung der integralen Form

$\operatorname{div} \mathbf E = \lim_{V \to 0} { 1 \over V } \oint_A \mathbf E \operatorname{d} \mathbf A = \lim_{V \to 0} { 1 \over V } { 1 \over \varepsilon_0 } \iiint_V \rho(\mathbf r) \operatorname{d} r = { 1 \over V } { 1 \over \varepsilon_0 } \rho(\mathbf r) V = { \rho(\mathbf r) \over \varepsilon_0 }$.

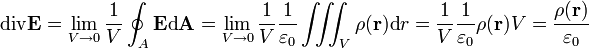Formulierung der differentiellen Form

Die differentielle Form des Gesetzes lautet

$\operatorname{div} \mathbf E = { \rho(\mathbf r) \over \varepsilon_0 }$.

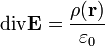Anwendung

Das gaußsche Gesetz bietet die Möglichkeit, zu einer gegebenen Ladungsverteilung auf oft sehr einfache Art das erzeugte Feld anzugeben. Auch das Coulombgesetz folgt direkt.

Hinweis auf die Poissongleichung

Das elektrische Feld besitzt ein Potential U. Es gilt:

$\mathbf E = - \operatorname{grad} U = - \nabla U$.

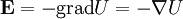Setzt man die differentielle Form ein, erhält man die Poisson-Gleichung.

$\operatorname{div} \mathbf E = \nabla \cdot \mathbf E = \nabla \cdot \left( - \nabla U \right ) = - \nabla \cdot \nabla U = - \Delta U = { \rho(\mathbf r) \over \varepsilon_0 }$

$\Leftrightarrow \Delta U = - { \rho(\mathbf r) \over \varepsilon_0 }$

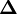wobei $\nabla$ der Nabla-Operator und $\mathbf{\Delta}$ der Laplace-Operator ist.

Außerdem liefert die Differentialrechnung, dass jede Lösung dieser Gleichung eindeutig bestimmt ist. Hat man also ein solches U gefunden, so beschreibt es auch das tatsächliche Feld.

Herleitung des Coulombgesetzes

Als Beispiel soll das Coulombgesetz für Punktladungen und kugelsymmetrische Ladungsanordnungen hergeleitet werden. Die Ladung Q sei als Punktladung gegeben, oder auch homogen auf eine Kugel verteilt. Man wählt als Oberfläche eine Kugel K mit dem Radius r um diese Anordnung. Es sei ε=1 (sehr gute Näherung für Luft). Auch das Feld muss kugelsymmetrisch sein (die Symmetrie des Problems gibt nichts anderes her), steht also überall senkrecht auf der Kugel. Man erhält

$\oint_K \mathbf E \; \mathrm d \mathbf A = { 1 \over \varepsilon_0 } Q \Leftrightarrow EA = { 1 \over \varepsilon_0 } Q \Leftrightarrow E 4 \pi r^2 = { 1 \over \varepsilon_0 } Q \Leftrightarrow E = { Q \over 4 \pi \varepsilon_0 } { 1 \over r^2 }$

und mit der Radialsymmetrie

$\mathbf E = { Q \over 4 \pi \varepsilon_0 } { 1 \over r^2 } \mathbf {e}_r$.

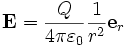Eine homogen geladene Kugel erzeugt also ein Feld, als ob die Ladung im Mittelpunkt säße.

Gravitation

Im Rahmen der Newton'schen Gravitationstheorie lassen sich die oben dargestellten Prinzipien ebenfalls auf das Gravitationsfeld anwenden. Die Gravitationsbeschleunigung einer Masse M ergibt sich aus dem Gravitationsgesetz zu

$\mathbf g=-\frac{GM}{r^2}\frac{\mathbf r}{r}$.

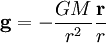Der Fluss durch die Oberfläche eines beliebigen Volumens ist dann

$\oint_A \mathbf g \, \mathrm d \mathbf A = -\oint_A \frac{GM}{r^2}\frac{\mathbf r}{r} \, \mathbf n \, \mathrm d A = -\oint_A \frac{GM}{r^2}\frac{\mathbf r}{r} \frac{\mathbf r}{r} \mathrm d A = -\oint_A \frac{GM}{r^2} \mathrm d A = -4 \pi G M$,

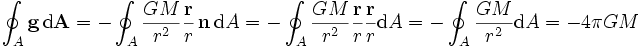wobei 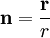$\mathbf n=\frac{\mathbf r}{r}$ der Normalenvektor ist.

Somit lässt sich das gravitative Beschleunigungsfeld einer Massenverteilung bestimmen mit

$\oint_A \mathbf g(\mathbf r) \mathrm d \mathbf A= - 4 \pi G M$.

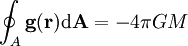In differentieller Form und für allgemeine Massenverteilungen ergibt sich

$\nabla \cdot \mathbf g = -4 \pi G \rho(\mathbf r)$,

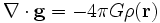was das gravitative Äquivalent der ersten Maxwellgleichung ist.