Gauß-Strahl

Das optische Konzept der Gauß-Strahlen (auch gaußsche Bündel genannt) verbindet Methoden der Strahlen- und Wellenoptik zur Beschreibung der Lichtausbreitung. Er ist eine Lösung der paraxial genäherten Helmholtz-Gleichung. Ein Gauß-Strahl zeichnet sich durch ein transversales Profil gemäß einer Gauß-Kurve (die Amplitude des elektromagnetischen Feldes nimmt mit dem Abstand zur Ausbreitungsachse exponentiell ab) und ein longitudinales Lorentz-Profil (er ist an einer Stelle, der Taille, fokussiert und „zerläuft“ mit zunehmendem Abstand zu ihr) aus.

Gauß-Strahlen beschreiben besonders gut die Lichtemission vieler Laser, aber sie lassen sich auch in vielen anderen Situationen elektromagnetischer Strahlung einsetzen. Besonders interessant sind sie, da sie Phasenbetrachtungen wie die Wellenoptik erlauben, aber einfachen Rechenmethoden der Strahlenoptik gehorchen.

Mathematische Beschreibung

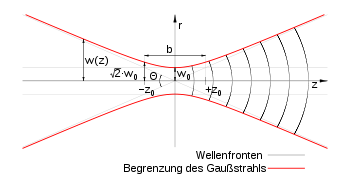
Zur mathematischen Beschreibung eines Gauß-Strahls verwendet man vorzugsweise Zylinderkoordinaten. Das Koordinatensystem wird so gewählt, dass die Ausbreitungsrichtung die z-Achse ist und die Strahltaille im Koordinatenursprung bei z = 0 liegt. Die komplexe Amplitude des elektrischen Feldes unter Berücksichtigung der Phase in Abhängigkeit vom Abstand r zur z-Achse und der Entfernung z zur Taille wird beschrieben durch die Funktion:

$E(r, z) = E_0 \; \frac{w_0}{w(z)} \cdot \mathrm{e}^{-\left(\frac{r}{w(z)}\right)^2} \cdot \mathrm{e}^{-i k \frac{r^2}{2R(z)}} \cdot \mathrm{e}^{i (\zeta(z) - k z)}$

Die zu dieser elektrischen Feldstärke gehörende Intensität ist dann:

$I(r, z) = I_0 \left(\frac{w_0}{w(z)} \right)^2 \mathrm{e}^{- \frac{2 r^2}{w^2(z)}}$

Dabei sind i die imaginäre Einheit mit i² = − 1, $k = \frac{2 \pi}{\lambda}$ die Kreiswellenzahl und E₀ bzw. I₀ die Werte an der Stelle (r = 0,z = 0). Die Parameterfunktionen w(z), R(z) und ζ(z) werden im folgenden definiert und beschreiben die Geometrie des Gauß-Strahles.

Die Intensität (Leistung pro Fläche) ist im Experiment schwerer zugänglich als die Leistung. Das Intensitätsmaximum I₀ lässt sich durch die Leistung P durch

$I_0 = \frac{2 P}{\pi w_0^2}$

schreiben. (Beweis durch Integration über die Fokalebene.)

Interpretation der Parameter

Transversales Profil

Gauß-Strahl (schematisch) mit Abmessungen, Strahlradius in rot und Wellenfronten auf der positiven z-Achse

Wie bereits erwähnt hat der Gauß-Strahl ein transversales Profil gemäß einer Gauß-Kurve. Als Strahlradius w definiert man bei einem bestimmten Wert z den Abstand zur z-Achse, an dem die Amplitude auf 1/e (ca. 36 %), die Intensität also auf 1/e², gefallen ist. Der minimale Strahlradius, der an der Taille des Strahls (also bei z = 0) vorliegt, wird mit w₀ bezeichnet. In Abhängigkeit vom Abstand z entlang der Achse verhält sich der Strahlradius dann im Nahfeld gemäß

$w(z) = w_0 \, \sqrt{1 + {\left( \frac{z}{z_0} \right)}^2 }$

mit der Rayleigh-Länge

$z_0 = \frac{\pi\cdot w_0^2}{\lambda}$

Axiales Profil

Im Abstand der Rayleighlänge von der Strahltaille ist der Strahl auf

$w(\pm z_0) = w_0 \sqrt{2}$

verbreitert. Die Rayleighlänge ist folglich der Abstand, bei dem sich die Strahlfläche in Bezug auf die kleinste Taille verdoppelt hat.

Der Abstand zwischen dem linken und rechten Punkt mit | z | = z₀ wird bi- oder konfokaler Parameter genannt:

$b = 2 z_0 = \frac{2 \pi w_0^2}{\lambda}$

Damit ist die Amplitude $|E(0,z_0)| = E_0 \frac{w_0}{w(z_0)} = \frac{1}{\sqrt{2}} \,E_0$ also an einer bestimmten z-Koordinate auf das $\tfrac{1}{\sqrt{2}}$-fache abgefallen. Dies entspricht einem Lorentz-Profil.

Krümmung

Radius der Wellenfronten über der Ausbreitungsrichtung. Für z→0 wird der Krümmungsradius unendlich, für großes z ergibt sich eine proportionale Abhängigkeit. Der kleinste Krümmungsradius liegt bei z₀.

Die Exponentialfunktionen mit imaginären Exponenten bestimmen die Phasenlage der Welle bei (r,z). Dabei bestimmt der Parameter R(z) anschaulich, wie stark die Phase an achsfernen Punkten verzögert ist, also, wie stark die Wellenfronten gekrümmt sind, und heißt deshalb Krümmungsradius. Er berechnet sich zu

$R(z) = z \, \left( 1+ {\left( \frac{z_0}{z} \right)}^2 \right) \ .$

Direkt in der Strahltaille für z = 0 ist der Krümmungsradius unendlich und es liegen ebene Wellenfronten vor. Im Vergleich zur ebenen homogenen Welle ist jedoch das Intensitätsprofil senkrecht zur Ausbreitungsrichtung nicht konstant, weshalb der Strahl außerhalb der Taille divergiert und die Wellenfronten sich krümmen.

Divergenz

Betrachtet man den Verlauf von w(z) für $z \gg z_0$, nähert er sich einer Geraden - dies zeigt die Verbindung zur Strahlenoptik auf. Wie stark der Gauß-Strahl verläuft, sich also transversal ausdehnt, lässt sich dann durch den Winkel (genauer: 'Steigung', da wegen Strahlparameterprodukt $w_0\theta=\frac{\lambda}{\pi}M^2$ auch Winkel > π / 2 für kleine Strahltaillen w₀ möglich $\rightarrow \tan (Winkel)$) zwischen dieser Geraden und der z-Achse angeben, dies nennt man die Divergenz:

$\theta_\mathrm{div} = \frac{\Theta}{2} = \arctan \left( \frac{w_0}{z_0} \right) = \arctan \left( \frac{\lambda}{\pi w_0} \right)$

Diese Beziehung führt zu dem Effekt, dass die Divergenz bei starker Fokussierung größer wird: ist die Strahltaille schmal, verläuft der Strahl in großen Entfernungen stark auseinander. Man muss also einen Kompromiss aus Fokussierung und Reichweite finden.

Gouy-Phase

In der Wellenphase taucht auch ein Term auf, der die Gouy-Phase des Gauß-Strahls genannt wird:

$\zeta(z) = \arctan \left( \frac{z}{z_0} \right) \ .$

Diese liefert einen Phasenunterschied von π beim Übergang von $\,z < -z_0$ zu $\,z > z_0$, was dem „Umklappen“ der klassischen Strahlenoptik im Fokus entspricht. Anschaulich beschreibt die Gouy-Phase die Phasenänderung des Gauß-Strahls beim Durchlaufen der Strahltaille verglichen mit einer ebenen Welle, die die gleiche Strecke durchläuft.

Matrizenoptik

Wenn ein Gaußstrahl auf Linsen oder Spiegel fällt, ist der resultierende Strahl wieder ein Gaußstrahl. Damit lassen sich die Regeln der Matrizenoptik aus der klassischen Optik vollständig übertragen. Definiert man den Parameter q(z) = z + iz₀, so wirkt die ABCD-Matrix eines optischen Elementes auf ihn gemäß

$q_1(z) = \frac{Aq_0 + B}{Cq_0 + D} \ .$

Komplizierte Kombinationen von optischen Elementen lassen sich zu einer Matrix zusammenfassen. Für die Berechnung von Laserresonatoren und Strahlengängen ist das ein großer Vorteil.

Siehe auch

• Beugungsmaßzahl

Literatur

• Dieter Meschede: Optik, Licht und Laser. 2. Auflage. Teubner B. G. GmbH, München 2005, ISBN 3519132486.
• Anthony E. Siegman: Lasers. 1. Auflage. University Science Books, 1986, ISBN 0-935702-11-3, Kapitel Wave Optics and Gaussian Beams.
• Eugene Hecht: Optik. 4. Auflage. Oldenbourg Wissenschaftsverlag, München 2005, ISBN 3486273590.
• Herwig Kogelnik, Tingye Li: Laser beams and Resonators. In: Applied Optics. Vol. 5, Nr. 10, 1966, S. 1550-1567, doi:10.1364/AO.5.001550.

Weblinks

• Fokussierung und Aufweitung von Laserstrahlung, Linos Katalogauszug (PDF-Datei; 84 kB)
• Gaussian Beam Propagation, Melles-Griot Katalogauszug (PDF-Datei; 276 kB)