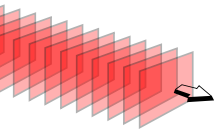
Ebene Welle

Eine ebene Welle ist eine im Raum fortschreitende Welle, deren Flächen gleicher Phase, also ihre Wellenfronten, Ebenen sind. Gleichbedeutend damit ist, dass die Ausbreitungsrichtung der Welle überall dieselbe ist.

Ebene Welle.

Meistens ist mit der Bezeichnung auch eine konstante Amplitude der Welle in Raum und Zeit, eine feste Frequenz und ein sinusförmiger Verlauf gemeint. Solche homogenen ebenen Wellen gehören zu den einfachsten Lösungen von Wellengleichungen, wie sie in der klassischen Mechanik, in der Elektrodynamik und in der Quantenmechanik auftreten, und werden oft als lokal gültige Näherungen für das Wellenfeld einer weit entfernten Quelle verwendet. Nicht ganz so einfache Lösungen von Wellengleichungen sind die Zylinderwelle und die Kugelwelle.

Mathematische Beschreibung einer ebenen Sinuswelle

Eine ebene Welle wird am einfachsten beschrieben, wenn das Koordinatensystem so gewählt wird, dass eine Achse der Ausbreitungsrichtung entspricht. In den Richtungen quer dazu gibt es keine Variation, sie können weggelassen werden. Eine Welle lässt sich darstellen als

$G(x,t) = \hat G \sin \left( 2\pi f \left( t - \frac{x}{c} \right) + \varphi_0 \right)$

Bei dieser bewegen sich die Punkte konstanter Phase mit der Geschwindigkeit c in die positive x-Richtung (in der inneren Klammer kompensiert das Anwachsen von x/c gerade das der Zeit t). Für eine Richtungsumkehr, wie sie etwa beim Radar auftritt, ist das Vorzeichen von x oder die x-Achse selbst umzudrehen (beides ist üblich und stiftet Verwirrung).

φ₀ ist die Phase der Welle für t = x = 0. Die Änderung der Phase (alle 2π wiederholt sich die Sinusfunktion) wird durch die Frequenz f bestimmt: Ein ortsfester Beobachter (festes x) sieht die Periodendauer T = 1/f, ein Schnappschuss dagegen (festes t) offenbart die Wellenlänge λ = c/f.

Die Physik der sich periodisch ändernden Größe G wird hier nicht weiter betrachtet. Es kann eine mechanische Auslenkung, eine Druckänderung, eine Feldstärke oder etwa eine Wahrscheinlichkeitsamplitude sein. Falls es sich um eine vektorielle Größe handelt, kann die Welle transversal sein – die Richtung ihrer Amplitude $\hat G$ gibt dann ihre Polarisation an.

Nicht immer ist es sinnvoll, die Information über die Phase im Argument der Sinusfunktion unterzubringen. Ändern sich beispielsweise Amplitude und Phase einer Welle durch den gleichen physikalischen Mechanismus, dann sind größere Phasenänderungen zu erwarten, wenn die Amplitude klein ist. Das lässt sich einfacher behandeln, indem die Welle in eine Sinus- und eine Kosinus-Komponente mit unabhängigen Amplituden zerlegt wird:

$G(x,t) = \hat G_A \sin \left( 2\pi f \left( t - \frac{x}{c} \right)\right) + \hat G_B \cos \left( 2\pi f \left( t - \frac{x}{c} \right)\right)$

Das ist recht unhandlich. Eine erste Sparmaßnahme ist die Einführung der Abkürzungen ω = 2πf und k = 2π/λ = ω/c, also

$G(x,t) = \hat G_A \sin (\omega t - kx) + \hat G_B \cos (\omega t - kx)$

Die zweite Sparmaßnahme vermeidet die Doppelung der Argumente, indem die Winkelfunktionen mit der Eulerformel cos φ + isin φ = e^iφ und die Vorfaktoren zu einer komplexen Amplitude zusammengefasst werden. Mit $\hat{\underline G} = \hat G_B + \mathrm{i}\,\hat G_A = |\hat G|\,\mathrm{e}^{\mathrm{i}\varphi_\mathrm{o}}$ kann man dann auch die Phase wieder getrennt notieren, je nach Problemstellung.

Anwendungen

Die nun kompakte Form der Gleichung,

$G(x,t) = \hat{\underline G} \mathrm{e}^{\mathrm{i}(\omega t - kx)},$

erlaubt Interpretationen: Ein bedeutsamer Schritt ist die Interpretation von kx als Skalarprodukt zweier Vektoren, einem Ortsvektor und dem Wellenvektor, der dann die Ausbreitungsrichtung der Welle im Raum angibt. Die Orientierung des Koordinatensystems ist dann – ohne Mehraufwand in der Notation – unabhängig von der Welle wählbar.

Unabhängig davon erlaubt die komplexe Exponentialfunktion eine Interpretation von k als komplexe Größe: Während der reelle Anteil die Periodizität der Welle bedingt, beschreibt der Imaginärteil ein exponentielles Abklingen oder Anwachsen der Welle. Da Abklingen der bei weitem häufigere Fall ist, siehe Absorptionsgesetz, lautet die Konvention, dass sich dies in einem positiven Imaginärteil ausdrücken soll. Dazu muss das Vorzeichen vor ikx positiv sein, denn das Produkt des positiven Imaginärteils mit der imaginären Einheit i ergibt einen negativen Wert, was im Exponenten für das gewünschte Abklingen sorgt. Damit sich dadurch nicht die Ausbreitungsrichtung ändert – weiterhin in die Richtung von k – muss auch das Vorzeichen vor iωt umgedreht werden, zusammen e ^{− i(ωt − kx)}. Dass sich dadurch der komplexe Zeiger andersherum dreht, hat keine physikalische Bedeutung, man muss in seinen Rechnungen nur darauf achten, dass man nicht Größen und Formeln miteinander kombiniert, die auf unterschiedlichen Konventionen basieren.

Im mehrdimensionalen Fall, mit k als Vektor, kann dessen imaginäre Komponente durchaus in eine andere Richtung zeigen als die reelle Komponente. Dies ist z. B. der Fall bei der Totalreflexion: Im dort rechten Bild läuft die evaneszente Welle (im optisch dünneren Medium rechts) nach oben, klingt aber nach rechts hin ab. In doppelbrechenden Medien hängt der Betrag des Wellenvektors von der Polarisationsrichtung und der Ausbreitungsrichtung ab.