Gerade und ungerade Funktionen

f(x) = x² – Beispiel für eine gerade Funktion: Die Normalparabel

f(x) = x³ - Beispiel für eine ungerade Funktion

Eine Funktion f mit Definitionsbereich D heißt in der Mathematik gerade Funktion genau dann, wenn f(x) = f( − x) $\forall x\in D$ gilt. Ist die Funktion reell, das heißt nimmt sie auf der nichtleeren Teilmenge $D\subseteq \R$ lauter reelle Werte an, dann ist ihr Schaubild achsensymmetrisch zur y-Achse.

Beispiele gerader Funktionen sind | x | , x², cos x und cosh x. Sie können keine Bijektion darstellen.

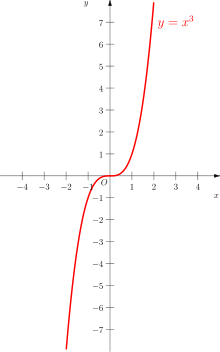
Eine Funktion f mit Definitionsbereich D heißt ungerade Funktion genau dann, wenn $f(-x) = -f(x)\,$ $\forall x\in D$ gilt. Im reellen Fall ist ihr Schaubild punktsymmetrisch zum Koordinatenursprung.

Beispiele ungerader Funktionen sind x, x³ und andere Potenzfunktionen mit ungeradem Exponenten sowie ganzrationale Funktionen, die die Summe von Potenzfunktionen mit ungeradem Exponenten darstellen. Aber auch beispielsweise die Funktionen sin x und sinh x.

Ist f eine ungerade Funktion, und ist $0\in D$, so gilt speziell f(0) = − f( − 0) = − f(0), also muss f(0) = 0 gelten. Die Funktion f(x) = 1 / x ist ein Beispiel einer ungeraden Funktion, die für x = 0 nicht definiert ist. Demnach gilt auch f(0) = 0 für sie nicht.

Die einzige reelle Funktion, die gleichzeitig gerade und ungerade ist, ist die Funktion, die konstant 0 ist, denn für diese gilt f(x) = f( − x) = − f( − x) = 0 $\forall x\in D$.

Ihre Bezeichnung haben die Funktionen daher, dass eine ganzrationale Funktion $f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n$ genau dann gerade ist, wenn nur Koeffizienten $a_0, a_2,\ldots a_{2k},\ldots$, also nur Koeffizienten zu Potenzfunktionen mit geradem Grad von 0 verschieden sind. Eine ganzrationale Funktion ist genau dann ungerade, wenn nur Koeffizienten zu Potenzfunktionen mit ungeradem Grad von 0 verschieden sind.

Eigenschaften gerader und ungerader Funktionen

• Die Summe zweier gerader Funktionen ist wieder gerade.
• Die Summe zweier ungerader Funktionen ist wieder ungerade.
• Das Produkt zweier gerader Funktionen ist wieder gerade.
• Das Produkt zweier ungerader Funktionen ist gerade.
• Das Produkt einer geraden und einer ungeraden Funktion ist ungerade.
• Die Komposition einer beliebigen Funktion mit einer geraden Funktion ist gerade.
• Die Komposition einer geraden Funktion mit einer ungeraden Funktion ist gerade.
• Die Komposition einer ungeraden Funktion mit einer ungeraden Funktion ist ungerade.
• Die Ableitung einer geraden Funktion ist ungerade, die Ableitung einer ungeraden Funktion ist gerade.
• Die Taylor-Reihe mit dem Entwicklungspunkt x = 0 einer geraden (ungeraden) Funktion enthält nur gerade (ungerade) Potenzen.
• Die Fourier-Reihe einer geraden (ungeraden) Funktion enthält nur Kosinus- (Sinus-) Terme.
• Jede Funktion g einer geraden Funktion f ist gerade, denn es gilt g(f( − x)) = g(f(x)).
• Eine beliebige Funktion lässt sich als Summe einer geraden und ungeraden Funktion wie folgt schreiben:

$f(x)=f_\mathrm{g}(x)+f_\mathrm{u}(x)=\frac{f(x)+f(-x)}{2} + \frac{f(x)-f(-x)}{2}$, mit

$f_\mathrm{g}(x)=\frac{f(x)+f(-x)}{2}$ dem geraden Anteil der Funktion f(x) und

$f_\mathrm{u}(x)=\frac{f(x)-f(-x)}{2}$ dem ungeraden Anteil der Funktion f(x).

• Berechnet man das bestimmte Integral einer ungeraden, in dem betrachteten Intervall stetigen Funktion, wobei die Grenzen symmetrisch um Null liegen, ergibt sich Null: $\int_{-a}^{a} f(x) dx=0$.

Siehe auch

• In der Schulmathematik gehört die Untersuchung eines Funktionsschaubildes auf Achsensymmetrie zur y-Achse und Punktsymmetrie zum Ursprung zu den ersten Schritten einer Kurvendiskussion.
• In der mathematischen Physik wird das Konzept der geraden und ungeraden Funktionen durch den Begriff der Parität verallgemeinert. Diese ist vor allem für Wellenfunktionen etwa in der Quantenmechanik von Bedeutung.

Literatur

• Marc Hensel: Kurvendiskussion. Lern- und Übungsbuch für die Abiturprüfung Mathematik. 1. Auflage. Books on Demand, Norderstedt 2010, ISBN 978-3-8391-4025-3.
• Harro Heuser: Lehrbuch der Analysis Teil 1. 8. Auflage. B. G. Teubner, Stuttgart 1988, ISBN 3-519-12231-6.

Weblinks

• Einfache Erläuterung der Kurvendiskussion mit Symmetrieuntersuchung für eine rationale Funktion
• Exemplarische Kurvendiskussion bei MathPlanet