Geschwindigkeitsänderung

Delta v (Δv) ist die Änderung (Delta oder Δ) der Geschwindigkeit (Vektor 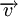$\overrightarrow{v}$) und wird in Strecke pro Zeit (m/s) angegeben. Sie ergibt sich aus der Subtraktion zweier Geschwindigkeiten,

$\Delta v = {|\overrightarrow v_2 - \overrightarrow v_1}|$ ,

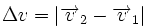wobei 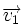$\overrightarrow{v_1}$ die Geschwindigkeit vor einem Ereignis und 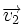$\overrightarrow{v_2}$ die Geschwindigkeit nach dem Ereignis ist. Da Δv aus der Differenz der Geschwindigkeitsvektoren berechnet wird, werden auch Änderungen der Richtung berücksichtigt, bei denen der Betrag der Geschwindigkeit gleich bleibt.

Raumfahrtdynamik

In der Raumfahrt ist Delta v, oft ausgeschrieben statt mit Formelzeichen, ein Maß für die Fähigkeit eines Raumfahrzeugs, Manöver auszuführen. Im einfachsten Fall, ohne Gravitationseinwirkung, ist Delta v das Integral der Beträge aller Geschwindigkeitsänderungen längs der gewünschten Trajektorie. Dieses Integral ist der Masse des Manöver ausführenden Raumfahrzeuges gegenüber invariant, ebenso wie gegenüber technischen Details dessen Antriebs. Die Invarianz der Größe hat offensichtliche Vorteile, so dass für Raumfahrzeuge statt Masse, Schub und Treibstoffvorrat das gesamte Delta v (Δv_max) angegeben wird, zu dem das Raumfahrzeug mit den vorhandenen Treibstoffresourcen fähig ist. Ist der Wert des verbleibenden Δv_max = 0, ist der gesamte Treibstoff verbraucht und keine Kursänderung mehr möglich.

Im Gravitationsfeld, z. B. beim Start oder bei einem Swing-by, entspricht das vom Raumfahrzeug aufzubringende Delta v keiner Geschwindigkeitsänderung direkt, kann aber als Größe dennoch berechnet werden. Es hängt in der Atmosphäre und in einer Nicht-Freifall-Situation allerdings zusätzlich von den aerodynamischen Eigenschaften des Fahrzeuges und der Zeit, die das Raumfahrzeug benötigt, um in einen stabilen Orbit, d. h. eine Freifall-Situation zu gelangen, ab. Für einen Start in einen Low Earth Orbit sind etwa 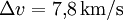$\Delta v = 7{,}8\,\mathrm{km/s}$ nötig, um die Geschwindigkeit von der Rotationsgeschwindigkeit an der Erdoberfläche auf die Orbitalgeschwindigkeit zu erhöhen. Dieser Anteil ist der Konstruktion des Raumfahrzeugs gegenüber invariant. Dazu kommen typischerweise 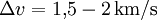$\Delta v = 1{,}5 - 2\,\mathrm{km/s}$ aufgrund des Luftwiderstandes und der Überwindung der Erdgravitation.

Es ist dabei zu beachten, dass bei dieser Angabe das Gewicht der Nutzlast (Gewicht der Personen an Bord / des Raumfahrzeugs) Einfluss auf das verfügbare DeltaV eines Raumschiffes hat, da mit Zunahme der Masse und der damit gesteigerten Trägheit das verfügbare DeltaV kleiner wird. Mit anderen Worten: Hätten die Astronauten bei den Apollomissionen zu viele Mondsteine eingepackt, würde zwar das benötigte DeltaV der Aufstiegsstufe, um das Mutterschiff zu erreichen, gleich bleiben, das DeltaV was zur Verfügung stünde würde aber abnehmen und den Wert des benötigten DeltaV unterschreiten, wodurch die Aufstiegsstufe zu schwer würde und das Mutterschiff nicht mehr erreichbar gewesen wäre.

Das Δv_max des voll betankten Apollo-Raumschiffs betrug beispielsweise bei maximaler Nutzlast 2804 m/s, das des Landemoduls 4690 m/s. Typische Delta v für orbitale und interplanetare Manöver sind:

Manöver	Bahnhöhe [km]	Typisches Delta-v pro Jahr [m/s]	Maximales Delta-v pro Jahr [m/s]
Positionsstabilisierung		50 – 55
Höhenstabilisierung (Luftwiderstand)	400 − 500	< 25	< 100
Höhenstabilisierung (Luftwiderstand)	500 – 600	< 5	< 25
Höhenstabilisierung (Luftwiderstand)	> 600		< 7,5
Lagekontrolle		2 – 6
Rotationskontrolle		5 – 10
Trennung von der Startstufe		5 – 10
Entlastung der Lagestabilistationskreisel		2 – 6

Manöver		Benötigtes Delta-v
Von	Nach	[m/s]
Erdoberfläche	Low Earth Orbit	9300 - 10.000
Low Earth Orbit	Geostationärer Transferorbit	2500
Geostationärer Transferorbit	Geostationärer Orbit	1500
Perigäum des Geostationären Transferorbits	Fluchtbahn	700
Fluchtbahn	Niedriger Mondorbit	700
Fluchtbahn	Mars-Transferorbit	600
Low Earth Orbit	Marsoberfläche	4800
Low Earth Orbit	Fluchtbahn aus dem Sonnensystem	8700
Niedriger Mondorbit	Mondoberfläche	1600

Siehe auch

• Raketengrundgleichung

Weblinks

• Delta-v Rechner für einfache Raketen (englisch)