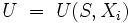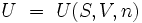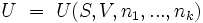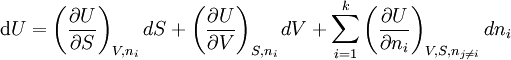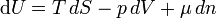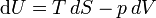Gibbssche Fundamentalgleichung

Die Fundamentalgleichung der Thermodynamik (auch Gibbssche Fundamentalgleichung genannt) ist Ausgangspunkt der formalen Thermodynamik. Sie ist die wichtigste charakteristische Funktion und beschreibt die Menge aller Gleichgewichtspunkte eines thermodynamischen Systems und zwar als Funktion der Zustandsgröße innere Energie U von allen extensiven Größen X_i.

$U\ =\ U(S,X_i)$

In nichtmagnetischen Einstoffsystemen vereinfachen sich die natürlichen Variablen zu Entropie S, dem Volumen V und der Stoffmenge n:

$U\ =\ U(S,V,n)$

Analog gilt dies auch für nichtmagnetische Mehrstoffsysteme mit k verschiedenen Stoffen:

$U\ =\ U(S,V,n_1, ..., n_k)$

Äquivalent kann die Funktion auch in der Form 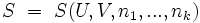$S\ =\ S(U,V,n_1, ..., n_k)$ angegeben werden.

Beide Funktionen beinhalten jeweils die gesamte thermodynamische Information des betrachteten Systems. Die mathematische Struktur der Thermodynamik ist damit festgelegt. Weitere, vor allem physikalische, Inhalte werden durch den Anschluss an die Hauptsätze gefunden. Häufig wird auch eine differentielle Schreibweise verwendet:

$\mathrm{d}U = \left( \frac{\partial U}{\partial S} \right)_{V,n_i} {d}S + \left( \frac{\partial U}{\partial V} \right)_{S,n_i} {d}V + \sum_{i=1}^k \left( \frac{\partial U}{\partial n_i} \right)_{V,S,n_{j \not= i}} {d}n_i$

(Kursiv bzw. nicht-kursiv geschriebene Symbole (d bzw. d) sollen dabei partielle und totale Differentiale unterscheiden.)

Mit der Definition für die Temperatur, den Druck und das chemische Potential folgt:

$\mathrm{d}U = T\, {d}S - p\, {d}V + \mu\, {d}n \!$

Unter der Voraussetzung einer konstanten Stoffmenge vereinfacht sich dies weiter zu:

$\mathrm{d}U = T\, {d}S - p\, {d}V \!$

Hieraus geht deutlich hervor, dass die Zustandsgleichungen im Prinzip die ersten Ableitungen der Fundamentalgleichung sind. Aus mathematischen Sätzen über differenzierbare Funktionen mehrerer Variablen können Beziehungen der zweiten Ableitungen gefunden werden: die Maxwell-Beziehungen.

Aus den zweiten Ableitungen der Fundamentalrelation können die experimentell wichtigen Antwortkoeffizienten, wie z. B. spezifische Wärmekapazität, Kompressibilität und Wärmeausdehnungskoeffizient hergeleitet werden.

Die Legendre-Transformationen der Fundamentalrelation führt auf die thermodynamischen Potentiale: Freie Energie, Enthalpie und Freie Enthalpie.

Siehe auch

• charakteristische Funktion (Physik)