Intuitionistische Logik

Der Intuitionismus (eine Art des Konstruktivismus) ist eine von L. E. J. Brouwer begründete Richtung der Philosophie der Mathematik, bei der die Mathematik als freie, rein intuitive Tätigkeit des exakten Denkens angesehen wird und die den Standpunkt vertritt, der Wahrheitsbegriff solle auf beweisbare Aussagen beschränkt werden.

Grundgedanke

Die Wahrheit eines mathematischen Satzes wird im Intuitionismus gleichgesetzt mit einem Denkprozess in Bezug auf seinen Beweis, der nur durch die innere Zeit des menschlichen Geistes gesteuert wird und an dessen Ende die Erkenntnis über die Wahrheit des Satzes steht. Wahrheit entsteht also erst durch die Verifizierung. Eine Wahrheit von Sätzen außerhalb der Verifizierung wird abgelehnt. Dies steht im Kontrast zur klassischen Philosophie (Platon, Ideenlehre), die annimmt, dass die Wahrheit von mathematischen Sätzen unabhängig von jeglichen (sowohl geistigen als auch physikalischen) Gegebenheiten sei.

L. E. J. Brouwer vertrat seinen philosophischen Standpunkt sehr emotional. Im Zusammenhang damit verwendete er in seinen Veröffentlichungen polemische, teilweise obskure Formulierungen.

Intuitionistische Logik

Die Gleichsetzung von Wahrheit und Beweisbarkeit führt zu einer anderen Interpretation von mathematischen Aussagen und damit zu einer anderen Logik. Während in der klassischen Logik die Aussage 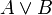$A\lor B$ wahrheitsfunktional (siehe Wahrheitswert) interpretiert wird als "A trifft zu, oder B trifft zu", wird dieselbe Aussage in der intuitionistischen Logik interpretiert als "Es gibt einen Beweis für A, oder es gibt einen Beweis für B".

Aus dieser unterschiedlichen Interpretation der Junktoren (Konnektive) ergibt sich, dass bestimmte Theoreme der klassischen Logik in der intuitionistischen nicht gültig sind. Ein Beispiel ist der Satz vom ausgeschlossenen Dritten, 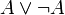$A\lor \neg A$. Die klassische Interpretation lautet "A trifft zu, oder A trifft nicht zu" und ist leicht als gültig erkennbar. Die intuitionistische Interpretation lautet "A ist bewiesen, oder A ist widerlegt". Unter dieser Interpretation ist der Satz vom ausgeschlossenen Dritten offensichtlich nicht gültig, einerseits weil es Aussagen gibt, die weder bewiesen noch widerlegt sind, andererseits weil es Aussagen gibt, die überhaupt weder beweisbar noch widerlegbar sind.

Kalküle für die intuitionistische Logik müssen daher so beschaffen sein, dass in ihnen der Satz vom ausgeschlossenen Dritten nicht herleitbar ist. In einem Regelkalkül erreicht man das, indem man auf die Beseitigungsregel für die doppelte Negation verzichtet - für die Negation bleibt dann nur der Satz vom Widerspruch als Axiom oder als Regel. Auf diese Weise erhält man die intuitionistische Logik, welche den philosophischen Standpunkt in rein formaler Weise widerspiegelt.

• Joan Moschovakis: „Intuitionistic Logic“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)

Stellung bezüglich des mathematischen Konstruktivismus

Beweise nach intuitionistischen Paradigmen, die über die reine Logik hinausgehen und die Eigenschaften mathematischer Objekte untersuchen, führen zu einer konstruktiven Mathematik. Dies ergibt sich dadurch, weil ohne den Satz vom ausgeschlossenen Dritten keine Widerspruchsbeweise möglich sind, mit denen bei klassischer Logik die Existenz eines mathematischen Objektes bewiesen werden kann, indem die Nichtexistenz widerlegt wird. Der Intuitionismus gelangt insofern zu den gleichen Ergebnissen wie der Konstruktivismus, obwohl die dahinterliegenden philosophischen Betrachtungen unterschiedlich sind – der Intuitionismus begründet sich auf einem nicht-klassischen Wahrheitsbegriff, der Konstruktivismus auf einem nicht-klassischen Existenzbegriff.

Geschichte

Die Geschichte des Intuitionismus beginnt im Jahr 1912, als Luitzen Egbertus Jan Brouwer mit seiner Kritik am Gesetz des ausgeschlossenen Dritten seine philosophischen Grundlagen formuliert. Die erste vollständige Formalisierung intuitionistischer Aussagen- und Prädikatenlogik stellt Arend Heyting im Jahr 1930 vor. 1933 zeigte Kurt Gödel eine Übersetzungsmöglichkeit von klassischer in intuitionistische Logik auf. Eine Semantik für die intuitionistische Logik präsentiert als erster Saul Kripke. Weitere Logiker, die zum Intuitionismus beigetragen haben, sind Stephen Kleene und in Deutschland Paul Lorenzen.

Kritik des Intuitionismus an der klassischen Logik

Der Intuitionismus als philosophische bzw. metamathematische Richtung kritisiert nicht die klassische Logik als formales System, sondern stellt deren Anwendbarkeit auf wissenschaftliche, vor allem mathematische Fragestellungen in Frage bzw. vertritt die Meinung, dass andere logische Systeme diesen Fragestellungen angemessener sind.

Als eine philosophische Position, die das Konzept der Beweisbarkeit in die Mitte ihrer Überlegungen stellt, ist für den Intuitionismus die klassische Logik, die Junktoren (Konnektive) als Wahrheitsfunktionen (siehe Wahrheitswert) interpretiert, schlechthin nicht von Interesse, weil Beweisbarkeit nicht als Wahrheitsfunktion darstellbar ist.

Satz vom ausgeschlossenen Dritten

Der Satz vom ausgeschlossenen Dritten wird problematisch, wenn er sich auf unendliche Mengen bezieht. Als Beispiel diene hier der Satz

P: "Jede gerade Zahl, die größer als 2 ist, lässt sich als Summe von zwei Primzahlen darstellen".

Das Gegenteil dieses Satzes wird, nach der klassischen Logik, ausgedrückt durch den Satz

¬P: "Es gibt eine gerade Zahl, die größer als 2 ist und sich nicht als Summe von zwei Primzahlen darstellen lässt."

Weder der Satz P noch der Satz ¬P konnten bis heute bewiesen werden, siehe Goldbachsche Vermutung.

P kann nicht in der Weise bewiesen werden, dass für jede gerade Zahl g zwei Primzahlen p₁ und p₂ aufgeschrieben werden, deren Summe g ergibt. Denn es gibt ja unendlich viele gerade Zahlen. Nötig ist vielmehr ein Verfahren, das es erlaubt, in irgendeiner Weise aus der Zahl g, wie groß sie auch sei, die Zahlen p₁ und p₂ zu berechnen. Ein solches Verfahren ist heute aber nicht bekannt.

Um dagegen ¬P zu beweisen, müsste eine einzige gerade Zahl angegeben werden, für die die Zerlegung in zwei Primzahlen unmöglich ist. Da diese Primzahlen kleiner als g sein müssen, also nur endlich viele in Frage kommen, lässt sich dies für eine bestimmte Zahl g problemlos überprüfen. Bei allen Zahlen, bei denen diese Prüfung erfolgt ist, haben sich bisher solche Primzahlen p₁ und p₂ gefunden. Die Überprüfung kann aber grundsätzlich nicht an allen geraden Zahlen erfolgen, weil dies unendlich viele sind.

Aus Sicht der Intuitionisten besagt der „Satz vom ausgeschlossenen Dritten" nun, dass eine der beiden oben dargestellten Aufgaben, also der Beweis von P oder der Beweis von ¬P, durchführbar sein muss. Dies ist in der Tat nicht für alle Sätze P der Fall: Sollte eines Tages nun doch die Goldbachsche Vermutung bewiesen oder widerlegt werden, so gibt es dennoch viele andere Aussagen über unendliche Mengen, für die das gleiche Problem besteht (z.B. die Kontinuumshypothese); der Gödelsche Unvollständigkeitssatz zeigt zudem, dass solche Beispiele aus prinzipiellen Gründen existieren.

Der Satz vom ausgeschlossenen Dritten wird deshalb zwar in der klassischen Logik akzeptiert, nicht jedoch im Intuitionismus und der Güntherlogik.

Stellung der Mathematiker

David Hilbert äußerte im Jahr 1928 in Die Grundlagen der Mathematik seine Meinung über die Intuitionistische Logik: "Dieses Tertium non datur [=Satz vom ausgeschlossenen Dritten] dem Mathematiker zu nehmen, wäre etwa, wie wenn man dem Astronomen das Fernrohr oder dem Boxer den Gebrauch der Fäuste untersagen wollte."^[1]

Einzelnachweise

1. ↑ David Hilbert: Die Grundlagen der Mathematik, Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität, VI. Band (1928), S. 80

Literatur

• L. E. J. Brouwer, Begründung der Mengenlehre unabhängig vom logischen Satz vom ausgeschlossenen Dritten, in: ders., Collected Works, pp. 150-190, North-Holland Publishing Company, Amsterdam, Oxford 1975.
• L. E. J. Brouwer (Hrsg.), Intuitionismus, eingeleitet und kommentiert von Dirk van Dalen Mannheim, Leipzig, Wien, Zürich BI 1992, ISBN 3-411-15371-7

Weblinks

• Mark van Atten: „Luitzen Egbertus Jan Brouwer“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Mark van Atten: „The Development of Intuitionistic Logic“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)

Siehe auch

• Intuition
• Anschauung
• Intuitionismus (Ethik)
• Heyting-Algebra