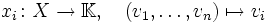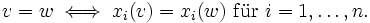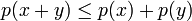- Hahn-Banach
-
Der Satz von Hahn-Banach (nach Hans Hahn und Stefan Banach) aus dem mathematischen Teilgebiet der Funktionalanalysis ist einer der Ausgangspunkte der Funktionalanalysis. Er sichert die Existenz von ausreichend vielen stetigen, linearen Funktionalen auf normierten Vektorräumen oder allgemeiner auf lokalkonvexen Räumen. Die Untersuchung eines Raums mit Hilfe der darauf definierten stetigen, linearen Funktionale führt zu einer weitreichenden Dualitätstheorie, die auf allgemeinen topologischen Vektorräumen in dieser Form nicht möglich ist, da eine zum Satz von Hahn-Banach analoge Aussage dort nicht gilt.
Darüber hinaus ist der Satz von Hahn-Banach die Grundlage für viele nicht-konstruktive Existenzbeweise wie z. B. im Trennungssatz oder im Satz von Krein-Milman.
Inhaltsverzeichnis
Der endlich-dimensionale Fall
Stellt man Vektoren eines endlichdimensionalen reellen oder komplexen Vektorraums X bzgl. einer fest gewählten Basis in der Form eines Zeilenvektors
 dar, so kann man die jeweiligen i-ten Einträge dieser Zeilenvektoren als Funktionen
dar, so kann man die jeweiligen i-ten Einträge dieser Zeilenvektoren als Funktionenauffassen (dabei sei
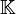 der Grundkörper
der Grundkörper 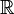 bzw.
bzw.  ). Ein wesentlicher Teil der Bedeutung einer solchen aus der linearen Algebra bekannten Koordinatendarstellung liegt nun darin, dass zwei Vektoren genau dann gleich sind, wenn alle ihre Koordinaten übereinstimmen:
). Ein wesentlicher Teil der Bedeutung einer solchen aus der linearen Algebra bekannten Koordinatendarstellung liegt nun darin, dass zwei Vektoren genau dann gleich sind, wenn alle ihre Koordinaten übereinstimmen:Die Koordinatenfunktionen trennen daher die Punkte, d. h. sind
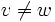 verschiedene Vektoren, dann gibt es einen Index i, so dass
verschiedene Vektoren, dann gibt es einen Index i, so dass  ist. Die xi sind stetige lineare Funktionale auf dem endlich dimesionalen Raum.
ist. Die xi sind stetige lineare Funktionale auf dem endlich dimesionalen Raum.In unendlich-dimensionalen Räumen gibt es i. d. R. keine den Koordinaten xi vergleichbare Konstruktion, wenn man dabei auf Stetigkeit der Koordinaten besteht. Der Satz von Hahn-Banach impliziert aber, dass die Menge aller stetigen linearen Funktionale auf einem normierten Raum (oder allgemeiner auf einem lokalkonvexen Raum) die Punkte trennt.
Formulierung
Es sei X ein Vektorraum über
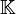 (dabei sei
(dabei sei 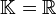 oder
oder 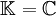 ).
).Eine Abbildung
heißt sublinear, wenn die Bedingungen
für alle
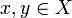 und
und 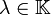 erfüllt sind.
erfüllt sind.Es seien nun
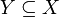 ein Teilraum;
ein Teilraum;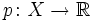 sublinear;
sublinear; ein lineares Funktional, für das
ein lineares Funktional, für das 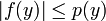 für alle
für alle  gilt.
gilt.
Dann gibt es ein lineares Funktional
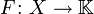 , so dass
, so dass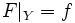 und
und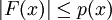
für alle
 gilt.
gilt.Der Beweis dieses grundlegenden Satzes ist nicht konstruktiv. Man betrachtet die Menge aller Fortsetzungen
 von f auf Teilräume Z mit
von f auf Teilräume Z mit 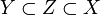 , für die
, für die 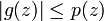 für alle
für alle  gilt. Dann zeigt man mit dem Lemma von Zorn, dass die Menge aller solchen Fortsetzungen maximale Elemente besitzt und dass ein solches maximales Element eine gesuchte Fortsetzung
gilt. Dann zeigt man mit dem Lemma von Zorn, dass die Menge aller solchen Fortsetzungen maximale Elemente besitzt und dass ein solches maximales Element eine gesuchte Fortsetzung 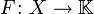 ist.
ist.Korollare
Häufig ist eine der folgenden Aussagen gemeint, wenn der „Satz von Hahn-Banach“ zitiert wird:
- Ist X ein normierter Raum, so gibt es für jedes
 ein lineares Funktional f mit Norm 1, für das
ein lineares Funktional f mit Norm 1, für das 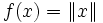 gilt. Sind
gilt. Sind 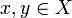 verschiedene Punkte, so erhält man die oben erwähnte Eigenschaft der Punktetrennung, indem man dies auf
verschiedene Punkte, so erhält man die oben erwähnte Eigenschaft der Punktetrennung, indem man dies auf 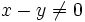 anwendet.
anwendet. - Ist allgemeiner X ein normierter Raum, U ein Unterraum, und liegt
 nicht im Abschluss von U, so gibt es ein lineares Funktional f mit Norm 1, das auf U verschwindet und für das
nicht im Abschluss von U, so gibt es ein lineares Funktional f mit Norm 1, das auf U verschwindet und für das 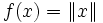 gilt.
gilt. - Ist X ein normierter Raum, Y ein Teilraum und f ein stetiges lineares Funktional auf Y, so kann f zu einem stetigen linearen Funktional derselben Norm auf ganz X fortgesetzt werden. Anders ausgedrückt: die Einschränkung von Funktionalen ist eine surjektive Abbildung
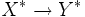 der Dualräume.
der Dualräume. - Weitere Folgerungen geometrischer Art finden sich im Artikel Trennungssatz.
Literatur
- Hans Hahn: Über lineare Gleichungssysteme in linearen Räumen. In: Journal für die reine und angewandte Mathematik 157 (1927), p. 214–229.
- Stefan Banach: Sur les fonctionelles linéaires. In: Studia Mathematica 1 (1929), p. 211–216.
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992
Wikimedia Foundation.