- Trennungssatz
-
Der Trennungssatz (auch Satz von Eidelheit) ist ein mathematischer Satz über die Möglichkeiten zur Trennung konvexer Mengen in normierten Vektorräumen (oder allgemeiner lokalkonvexen Räumen) durch lineare Funktionale. Dabei handelt es sich um geometrische Folgerungen aus dem Satz von Hahn-Banach.
Inhaltsverzeichnis
Erste Formulierung
Die einfachste Version des Trennungssatzes lautet wie folgt:
Sei X ein normierter Vektorraum (oder lokalkonvexer Raum) über
 oder
oder  . Seien weiter
. Seien weiter  eine abgeschlossene konvexe Menge und
eine abgeschlossene konvexe Menge und  . Dann existiert ein lineares stetiges Funktional
. Dann existiert ein lineares stetiges Funktional  mit
mit-
-
 .
.
-
Hier bezeichnet Re den Realteil und X' den Dualraum von X. Man sagt dann: Das Funktional φ trennt den Punkt x von der Menge M.
Weitere Formulierungen
In obiger Formulierung kann der Punkt x durch eine kompakte konvexe Menge ersetzt werden. Man erhält dann den folgenden Satz:
Sei X ein normierter Vektorraum (oder lokalkonvexer Raum) über
 oder
oder  . Seien weiter
. Seien weiter  eine nicht-leere, abgeschlossene, konvexe Menge und
eine nicht-leere, abgeschlossene, konvexe Menge und  eine nicht-leere, kompakte, konvexe Menge. Dann existiert ein lineares stetiges Funktional
eine nicht-leere, kompakte, konvexe Menge. Dann existiert ein lineares stetiges Funktional  mit
mit-
-
 .
.
-
Schließlich kommt man zu einer schwächeren Trennungseigenschaft, wenn man in obiger Version auf die Abgeschlossenheit und Kompaktheit verzichtet:
Sei X ein normierter Vektorraum (oder lokalkonvexer Raum) über
 oder
oder  . Seien weiter
. Seien weiter  nicht-leere, disjunkte, konvexe Mengen, M2 sei offen. Dann existiert ein lineares stetiges Funktional
nicht-leere, disjunkte, konvexe Mengen, M2 sei offen. Dann existiert ein lineares stetiges Funktional  mit
mit-
-
 .
.
-
Hyperebenen
Mengen der Form
 , wobei
, wobei  und
und  , sind abgeschlossene Hyperebenen. Sie zerlegen den Raum X in einen oberen Halbraum
, sind abgeschlossene Hyperebenen. Sie zerlegen den Raum X in einen oberen Halbraum  und einen unteren Halbraum
und einen unteren Halbraum  . Zu einer kompakten konvexen Menge und einer dazu disjunkten abgeschlossenen konvexen Menge kann man nach obigem Trennungssatz eine Hyperebene finden, so dass die beiden Mengen in unterschiedlichen Halbräumen liegen, und zwar jeweils im Inneren dieser Halbräume. Man sagt, die Hyperebene trenne die beiden konvexen Mengen. Das ist im 2-dimensionalen und 3-dimensionalen Fall besonders anschaulich, da die Hyperebenen in diesen Fällen Geraden bzw. Ebenen sind.
. Zu einer kompakten konvexen Menge und einer dazu disjunkten abgeschlossenen konvexen Menge kann man nach obigem Trennungssatz eine Hyperebene finden, so dass die beiden Mengen in unterschiedlichen Halbräumen liegen, und zwar jeweils im Inneren dieser Halbräume. Man sagt, die Hyperebene trenne die beiden konvexen Mengen. Das ist im 2-dimensionalen und 3-dimensionalen Fall besonders anschaulich, da die Hyperebenen in diesen Fällen Geraden bzw. Ebenen sind.Hat man zwei disjunkte konvexe Mengen in X, von denen eine offen ist, so gibt es zu diesen nach der zuletzt genannten Version des Trennungssatzes ebenfalls eine Hyperebene, so dass die beiden Mengen in unterschiedlichen Halbräumen liegen. Im Allgemeinen kann man aber nicht mehr erreichen, dass beide im Inneren der Halbräume liegen. Dazu betrachte man in
 die untere Halbebene
die untere Halbebene  und die offene Menge oberhalb des Graphen der Exponentialfunktion
und die offene Menge oberhalb des Graphen der Exponentialfunktion  . Wie durch nebenstehende Zeichnung verdeutlicht, ist
. Wie durch nebenstehende Zeichnung verdeutlicht, ist  mit φ(x,y): = y die einzige trennende Hyperebene, und M1 liegt nicht im Inneren des zugehörigen Halbraums.
mit φ(x,y): = y die einzige trennende Hyperebene, und M1 liegt nicht im Inneren des zugehörigen Halbraums.Anwendungen
Dieser Satz hat auch außerhalb der Funktionalanalysis viele wichtige Anwendungen und stellt für viele Beweise ein nicht-konstruktives Existenzargument dar, unter anderem:
- Existenz von Subdifferentialen für geeignet formulierte verallgemeinerte Richtungsableitungen.
- Beweis von Farkas’ Lemma, das heißt Anwendung in der konvexen Optimierung.
- Beweis des Fundamentalsatzes der Preistheorie für faire Preise von Derivaten im Mehr-Perioden-Modell.
Literatur
- R.V. Kadison, J. R. Ringrose: Fundamentals of the Theory of Operator Algebras, 1983
- Dirk Werner: Funktionalanalysis, 2. Auflage, Springer, Berlin Heidelberg New York, 1997, ISBN 3-540-61904-6
-
Wikimedia Foundation.

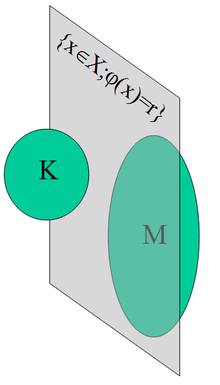
 werden disjunkte konvexe Mengen durch Ebenen getrennt.
werden disjunkte konvexe Mengen durch Ebenen getrennt.