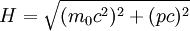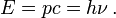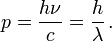Energiequant

Photon
Klassifikation
Elementarteilchen Boson Eichboson
Eigenschaften
Ladung	0 C
Spin	1

Das Photon (von Griechisch φως phōs, Gen. φωτός phōtos „Licht“) ist die elementare Anregung (Quant) des quantisierten elektromagnetischen Feldes. In der Physik ist es eines der Studienobjekte der Quantenelektrodynamik, des ältesten Teils des Standardmodells der Teilchenphysik. Anschaulich gesprochen sind Photonen die „Bausteine“ elektromagnetischer Strahlung, so etwas wie „Lichtteilchen“. Allerdings darf dabei nicht vergessen werden, dass alle bewegten (Elementar-) Teilchen einschließlich der Photonen auch Welleneigenschaften besitzen, dies nennt man Welle-Teilchen-Dualismus. Photonen gehören zur Gruppe der Bosonen.

Symbol

Für das Photon wird im allgemeinen das Symbol γ (gamma) verwendet. In der Hochenergiephysik ist dieses Symbol allerdings reserviert für die hochenergetischen Photonen der Gammastrahlung (Gamma-Quanten) und die in diesem Zweig der Physik ebenfalls relevanten Röntgenphotonen erhalten das Symbol X (von Englisch: X-ray). 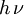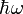Sehr oft wird ein Photon auch durch die enthaltene Energie mit $h \, \nu$ oder $\hbar \omega$ dargestellt. 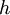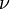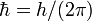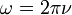Darin sind $\, h$ das plancksche Wirkungsquantum und $\, \nu$ die (Licht-)Frequenz, in der zweiten Schreibweise sind $\hbar = h / (2 \pi)$ und $\, \omega = 2 \pi \nu$ die Kreisfrequenz.

Eigenschaften

Jegliche elektromagnetische Strahlung, von Radiowellen bis zur Gammastrahlung, ist in Photonen quantisiert. Das bedeutet, die kleinste Menge an elektromagnetischer Strahlung beliebiger Frequenz ist ein Photon. Photonen haben eine unendliche natürliche Lebensdauer, können aber bei einer Vielzahl physikalischer Prozesse erzeugt oder vernichtet werden. Ein Photon befindet sich nie in Ruhe, sondern bewegt sich immer mit Lichtgeschwindigkeit. Daraus folgt, dass es keine Ruhemasse besitzen kann. In optischen Medien ist die effektive Lichtgeschwindigkeit im Vergleich zur Vakuumlichtgeschwindigkeit aufgrund der Wechselwirkung der Photonen mit der Materie verringert. Da Photonen Energie besitzen, wechselwirken sie gemäß der Allgemeinen Relativitätstheorie mit der Gravitation.

Erzeugung und Detektion

Photonen können auf vielerlei Arten erzeugt werden, insbesondere durch Übergänge („Quantensprünge“) von Elektronen zwischen verschiedenen Zuständen (z. B. verschiedenen Atom- oder Molekülorbitalen oder Energiebändern in einem Festkörper). Photonen können auch bei nuklearen Übergängen, Teilchen-Antiteilchen-Vernichtungsreaktionen (Annihilation) oder durch beliebige Fluktuationen in einem elektromagnetischen Feld erzeugt werden.

Zum Nachweis von Photonenströmen können z. B. Photomultiplier, Photoleiter oder Photodioden verwendet werden. CCDs, Vidicons, PSDs, Quadrantendioden oder Foto-Platten und Filme werden zur ortsauflösenden Detektion von Photonen benutzt. Im IR-Bereich werden auch Bolometer eingesetzt. Photonen im Gammastrahlen-Bereich können durch Geigerzähler einzeln nachgewiesen werden. Photomultiplier und Avalanche-Photodioden können auch zur Einzelphotonendetektion im optischen Bereich verwendet werden, wobei Photomultiplier im Allgemeinen die niedrigere Dunkelzählrate besitzen, Avalanche-Photodioden aber noch bei niedrigeren Photonenenergien bis in den IR-Bereich einsetzbar sind.

Masse

Die Ruhemasse eines Photons wird zu Null angenommen. Dies ergibt sich zum einen aus der Art des elektromagnetischen Potentials und zum anderen aus der Lichtgeschwindigkeit, mit der Photonen im Vakuum unterwegs sind.

• Wären Photonen massebehaftet, so wäre das elektrische Potential kein Coulomb-Potential, sondern ein Yukawa-Potential. Das Potential einer elektrischen Ladung wäre also mit einem zusätzlichen exponentiellen Dämpfungsterm abgeschwächt. Weiterhin würde eine Photonmasse das Verhalten von Magnetfeldern ändern. Solche Abweichungen konnten bislang nicht experimentell nachgewiesen werden, woraus sich die momentan (Stand 2007) bestehenden Obergrenzen für die Photonmasse ergeben^[1].

• Die spezielle Relativitätstheorie verbietet nicht nur das Erreichen der Lichtgeschwindigkeit c für jedes Objekt, dessen Ruhemasse m₀ größer als Null ist, sondern liefert auch den direkten mathematischen Nachweis, dass sich masselose Teilchen mit Lichtgeschwindigkeit bewegen.

Die relativistische Gesamtenergie (Hamiltonfunktion) eines Teilchens ist

$H=\sqrt{(m_0 c^2)^2 + (pc)^2}$

Im Hamilton-Formalismus ist die Geschwindigkeit die Ableitung der Hamiltonfunktion nach dem generalisierten Impuls

$v=\frac{\mathrm dH}{\mathrm dp}=\frac{p c^2}{\sqrt{(m_0 c^2)^2 + (pc)^2}} = c$,

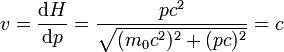wobei hier für Photonen v=c gesetzt wurde. Diese Gleichung ist jedoch nur dann erfüllt, wenn m₀ = 0 ist.

Allerdings hat das Photon eine Energie 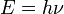$\, E = h \nu$. Ein Photon mit entsprechender Mindestenergie kann z. B. bei Wechselwirkung mit einem Atomkern über Paarerzeugung in ein Teilchen-Antiteilchen-Paar übergehen. Infolge der Energieerhaltung und der Äquivalenz von Masse und Energie 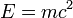$\, E = mc^2$ ist damit die Masse der entstehenden Materie gegeben.

Spin

Während etwa der Elektronenspin parallel oder antiparallel zu einer beliebig vorgegebenen Richtung ist^[2], kann der Photonenspin wegen fehlender Ruhemasse nur zirkular, also parallel oder antiparallel zur Flugrichtung orientiert sein. Dennoch kann auch ein einzelnes Photon linearpolarisiert werden, indem zwei entgegengesetzt zirkularpolarisierte Zustände überlagert werden.

Photonen sind Spin-1 Teilchen und somit Bosonen. Es können also beliebig viele Photonen denselben quantenmechanischen Zustand besetzen, was zum Beispiel in einem Laser realisiert wird. Photonen vermitteln die elektromagnetische Wechselwirkung: Sie sind die Teilchen, die es anderen Teilchen erlauben, miteinander elektromagnetisch wechselzuwirken. Da die elektromagnetische Wechselwirkung eine sogenannte Eichtheorie ist, zählen die Photonen zu den Eichbosonen.

Photonen im Vakuum

Im Vakuum bewegen sich Photonen mit der Vakuumlichtgeschwindigkeit c = 299792458 ms⁻¹. Die Dispersionsrelation, d. h. die Abhängigkeit der Energie 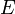$E\,$ von der Frequenz ν (ny), ist linear, und die Proportionalitätskonstante ist das Plancksche Wirkungsquantum h,

$E = pc = h\nu\,.$

Zahlenwerte, wie sie in optischen Spektren typischerweise auftreten, können wie folgt ermittelt werden:

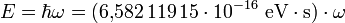$E = \hbar \omega = (6{,}582\,119\,15 \cdot 10^{-16}\ \mathrm{eV \cdot s}) \cdot \omega$ ,  E dabei in eV (Elektronenvolt), ω in s⁻¹ (Kreisfrequenz), 1 eV entspricht etwa einem ω von 1,520 · 10¹⁵ s⁻¹

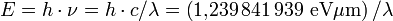$E = h \cdot \nu = h \cdot c / \lambda = \left(1{,}239\,841\,939\ \mathrm {eV\mu m}\right) / \lambda$ ,   E dabei in eV (Elektronenvolt), λ in μm (Wellenlänge), 1 eV entspricht etwa 1,240 μm = 1240 nm

Der Impuls p eines Photons beträgt damit

$p=\frac{h \nu}{c}=\frac{h}{\lambda}\,.$

Photonen in Medien

In einem Material wechselwirken Photonen mit dem sie umgebenden Medium, woraus sich veränderte Eigenschaften ergeben. Das Photon kann absorbiert werden, wobei seine Energie natürlich nicht verschwindet, sondern in elementare Anregungen (Quasiteilchen) des Mediums wie Phononen oder Exzitonen übergeht. Möglich ist auch, dass es sich durch ein Medium ausbreitet, zum Beispiel als gekoppeltes Phonon-Photon-Paar (Polariton). Diese elementaren Anregungen in Materie haben üblicherweise keine lineare Dispersionsrelation, und ihre Ausbreitungsgeschwindigkeit ist niedriger als die Vakuumlichtgeschwindigkeit bis hin zu nur einigen Metern pro Sekunde für spezielle Materialien.

Wechselwirkung von Photonen mit Materie

Photonen, die auf Materie treffen, lösen bei bestimmten Energien unterschiedliche Prozesse aus. Im Folgenden sind für verschiedene Prozesse die Energiebereiche angegeben, in denen sie relevant sind:

• unter 1 eV nur Wärmeentwicklung (Wärmestrahlung), keine Ionisation
• 1 eV bis 100 keV Photoeffekt,
• 50 keV bis 1 MeV Compton-Effekt,
• 1,022 bis 6 MeV Paarbildung,
• 2,18 bis 16 MeV Kernphotoeffekt.
• höhere Energien: Photodesintegration

Diese Effekte tragen maßgeblich dazu bei, dass man diese Strahlung detektieren kann und sich bestimmte Stoffe mit bestimmten Effekten anhand der Gammaspektroskopie nachweisen lassen.

Forschungsgeschichte

Seit der Antike gab es verschiedene, oft einander widersprechende Vorstellungen über die Natur des Lichts. Im 19. Jahrhundert konkurrierten Wellen- und Teilchentheorien. Während viele Phänomene wie Interferenz- und Polarisationserscheinungen für eine Wellennatur des Lichts sprachen, gab es auch Indizien für einen Teilchencharakter. Ein historisch sehr wichtiges Experiment, welches auf eine Teilchennatur des Lichts hinwies, war im Jahre 1887 die Beobachtung des Photoelektrischen Effekts durch Heinrich Hertz und Wilhelm Hallwachs.

Die Quantisierung der elektromagnetischen Strahlung geht letztendlich auf die Erklärung der Schwarzkörperstrahlung durch Max Planck im Jahr 1900 zurück (plancksches Strahlungsgesetz). Planck selbst stellte sich allerdings nicht die elektromagnetische Strahlung an sich quantisiert vor, sondern erklärte die Quantisierung damit, dass die Oszillatoren in den Wänden der Schwarzkörperresonatoren nur diskrete Energiemengen mit dem elektromagnetischen Feld austauschen können.

Albert Einstein beschrieb 1905 in seiner Publikation zum photoelektrischen Effekt das Licht als aus Lichtquanten mit Partikeleigenschaften bestehend (für diese Arbeit wurde er 1921 mit dem Nobelpreis ausgezeichnet). Die formale Quantentheorie des Lichtes wurde erst seit 1925 beginnend mit Arbeiten von Max Born, Pascual Jordan und Werner Heisenberg entwickelt. Die bis heute gültige Theorie der elektromagnetischen Strahlung, welche auch die Lichtquanten beschreibt, die Quantenelektrodynamik (QED), geht in ihren Anfängen auf eine Arbeit von Paul Dirac im Jahr 1927 zurück, in der er die Wechselwirkung von quantisierter elektromagnetischer Strahlung mit einem Atom beschreibt. Die QED wurde in den 1940er Jahren entwickelt und 1965 mit der Verleihung des Nobelpreises für Physik an Richard P. Feynman, Julian Schwinger und Shinichirō Tomonaga gewürdigt.

Der Begriff Photon wurde 1926 durch den Chemiker Gilbert Newton Lewis geprägt, der darunter aber nicht das Lichtquant verstand. Er verwandte den Begriff im Rahmen eines von ihm vorgeschlagenen (und allgemein nicht anerkannten) Modells der Wechselwirkung von Atomen mit Licht.

Literatur

• Chandrasekhar Roychoudhuri, Rajarshi Roy: The nature of light: What is a photon? In: Optics and Photonics News 14 (2003), Nr. 10 SUPPL., S. 49–82 [1], ISSN 1047-6938
• Harry Paul: Photonen: Eine Einführung in die Quantenoptik. 2. Aufl. Stuttgart: Teubner, 1999 (Teubner-StudienbücherPhysik). – ISBN 3-519-13222-2
• Klaus Hentschel: Einstein und die Lichtquantenhypothese. Naturwissenschaftliche Rundschau 58(6), S. 311–319 (2005). – ISSN 0028-1050
• Liang-Cheng Tu, Jun Luo, George T. Gillies: The mass of the photon. In: Reports on Progress in Physics 68 (2005), Nr. 1, S. 77–130. – doi:10.1088/0034-4885/68/1/R02

Weblinks

• Welt der Physik zur Welle-Teilchen-Natur des Lichts
• HydrogenLab 3D Animationen von atomaren Übergängen: Absorption und Emission von Photonen (semiklassisch)
• QuantumLab Experimente mit einzelnen Photonen: Beweis der Existenz, Quantenzufall, Verschränkung,...

Einzelnachweise

1. ↑ Particle Data Group, Eigenschaften des Photons PDF
2. ↑ Siehe z.B. pro-physik.de über Spin-Hall-Effekt jetzt auch mit Photonen