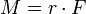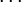- Hebelarm
-
Physikalische Größe Name Moment Größenart Moment Formelzeichen der Größe M Größen- und
Einheiten-
systemEinheit Dimension SI Newtonmeter (Nm) M·L2·T −2·1 Siehe auch: Kraftmoment, Drehmoment, Torsionsmoment (MT, T) Das Moment ist in der Mechanik die drehende Wirkung, die von einem entgegengesetzt gerichteten, gegeneinander in der Wirkungslinie versetzten Paar gleich großer Kräfte ausgeübt wird. Den senkrechten Abstand der Wirkungslinien der beiden Kräfte bezeichnet man als Hebelarm. Die Größe des Moments ist das Produkt aus einer der beiden Kräfte und dem senkrechten Abstand der Wirkungslinien der Kräfte:
Der Drallsatz beschreibt die zeitliche Änderung des Moments.
Inhaltsverzeichnis
Der Momentenvektor
Das Moment ist als Vektor darstellbar, der mit der Ebene, die von beiden Wirkungslinien gebildet wird, einen rechten Winkel bildet (Kreuzprodukt).
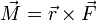 – Momentenvektor
– Momentenvektor
Die Richtung des Momentenvektors ist per Definition diejenige Richtung, in der eine Schraube mit Rechtsgewinde fortschreiten würde. Man bezeichnet dies auch als Rechte-Hand-Regel: die gekrümmten Finger zeigen in Drehrichtung, und der Daumen in Richtung des Momentenvektors. Der Momentenvektor wird im Unterschied zum Kraftvektor, der eine „Spitze“ hat, mit zwei übereinander angeordneten Spitzen dargestellt.
Dimension und Maßeinheit
Die physikalische Dimension des Moments ist demnach das Produkt aus Kraft und Hebelarm. Im SI-System hat ein Moment die abgeleitete Maßeinheit Newtonmeter (Nm), gleichbedeutend mit
 .
.- Die Einheit des Momentes ist auch die der physikalischen Arbeit. Allerdings muss das Moment um einen Winkel drehen, um Arbeit zu leisten, das Moment ist also mit dem dimensionslosen Winkel (in der dimensionslosen SI-Einheit Radiant) zu multiplizieren. Es werden also zwei verschiedene physikalische Größen mit der Einheit Newton mal Meter beschrieben.
Definition
Eine Kraft
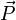 , die in einem Punkt A angreift, kann man mit einer gleichen Kraft
, die in einem Punkt A angreift, kann man mit einer gleichen Kraft  und entgegengesetzt gleicher Kraft
und entgegengesetzt gleicher Kraft 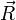 ergänzen, die beide im Punkt B angreifen und sich dort gegenseitig aufheben. Betrachtet man nun
ergänzen, die beide im Punkt B angreifen und sich dort gegenseitig aufheben. Betrachtet man nun  als eine von A nach B verschobene Version der Kraft
als eine von A nach B verschobene Version der Kraft 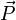 , ergibt sich, dass zusätzlich ein Moment aus dem Kräftepaar
, ergibt sich, dass zusätzlich ein Moment aus dem Kräftepaar 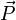 und
und 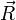 entsteht. Das Moment ist in der folgenden Skizze ein Vektor, der in die Ebene hineinzeigt, und beträgt
entsteht. Das Moment ist in der folgenden Skizze ein Vektor, der in die Ebene hineinzeigt, und beträgt  , also das Kreuzprodukt aus dem Ortsvektor des Kraftangriffspunktes und dem Kraftvektor. (Vektoren in der folgenden Skizze durch Fettdruck gekennzeichnet.)
, also das Kreuzprodukt aus dem Ortsvektor des Kraftangriffspunktes und dem Kraftvektor. (Vektoren in der folgenden Skizze durch Fettdruck gekennzeichnet.)A A A P ---->o o P ---->o | | | | = | + | | | | o Q ---->o o<---- R B B B
Wenn an einem Körper sehr viele Kräfte
 in den Punkten
in den Punkten  wirken, rechnet man sie in diesem Sinne auf einen gemeinsamen Bezugspunkt
wirken, rechnet man sie in diesem Sinne auf einen gemeinsamen Bezugspunkt  um, indem man sie alle dorthin verschiebt und gleichzeitig die Momente einführt:
um, indem man sie alle dorthin verschiebt und gleichzeitig die Momente einführt:Freie, unfreie und unterbundene Bewegung
Wenn der Körper irgendwo befestigt ist, schneidet man ihn (in Gedanken) frei und bezieht die Schnittlasten in die Betrachtung mit ein. Schnittlasten sind die von der weggeschnittenen Umgebung auf den Körper ausgeübten Kräfte und Momente. Der Körper befindet sich im Gleichgewicht, wenn nicht nur alle (in den gemeinsamen Bezugspunkt umgerechneten) Kräfte in der Summe null sind, sondern auch alle Momente (die beim Verschieben der Kräfte in den Bezugspunkt hinzukommen):
Bei den folgenden Größen geht es also nicht um die Bewegung, sondern um die Belastung und Deformation der Körper; in der Technik werden sie daher nicht als Drehmoment, sondern als Moment bezeichnet:
- Einspannmoment eines Kragträgers
- krängendes Moment des Windes auf ein Segelboot
In Wellen, Trägern und anderen Balken unterscheidet man die Schnittmomente:
- Biegemoment, Momentenvektor quer zur Achse, Balken wird gekrümmt
- Torsionsmoment, Momentenvektor in Achsrichtung, Balken wird verdrillt
Man betrachtet dabei einen Teil des Balkens, von dem der restliche Balken (in Gedanken) weggeschnitten wurde, und definiert die Schnittkräfte und Schnittmomente als Komponenten des Kraftvektors und des Momentenvektors, den der weggeschnittene Teil auf das Schnittufer ausübt.
- Direktionsmoment, das spezifische Rückstellmoment einer Feder
Anderenfalls wird der Körper durch die Kräfte und Momente translatorisch und/oder rotatorisch beschleunigt. Hierbei wählt man als körperfesten Bezugspunkt am zweckmäßigsten den Schwerpunkt (Massenmittelpunkt) am Ort
 . Ein beliebiger Punkt des Körpers hat die Geschwindigkeit
. Ein beliebiger Punkt des Körpers hat die Geschwindigkeit
- wobei der Drehgeschwindigkeitsvektor
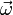 nach der Rechte-Hand-Regel in Richtung des Daumens zeigt, wenn die Fingerspitzen in Drehrichtung zeigen.
nach der Rechte-Hand-Regel in Richtung des Daumens zeigt, wenn die Fingerspitzen in Drehrichtung zeigen.
- Der zentrische, also translatorische Anteil heißt das Schubmoment
- Der azentrische, also rotative ist das Drehmoment oder Drall
- Die Momente der angreifenden Kräfte werden dann Antriebsmoment und Bremsmoment, Abtriebsmoment oder ähnlich benannt, je nachdem, ob der zentrische Anteil in oder gegen den Geschwindigkeitsvektor oder der azentrische Anteil in oder gegen die Drehrichtung wirkt.
Der Drallsatz
Der Drallsatz
kann unter der Annahme, dass zwischen den Punktmassen nur zentrale Kräfte wirken (d. h. die Kräfte zwischen den Punktmassen wirken entlang der Verbindungslinie) durch Integration über alle Punktmassen hergeleitet werden. Es sei deshalb angemerkt, dass der Drallsatz nicht bewiesen werden kann.
Darin ist m die Masse des Körpers.
 ist der Massenträgheitstensor, im Allgemeinen ein Tensor zweiter Stufe, darstellbar als 3×3 Matrix. Seine Komponenten sind die im körperfesten System zeitlich konstanten Massenträgheits- und Deviationsmomente.
ist der Massenträgheitstensor, im Allgemeinen ein Tensor zweiter Stufe, darstellbar als 3×3 Matrix. Seine Komponenten sind die im körperfesten System zeitlich konstanten Massenträgheits- und Deviationsmomente.Im einfachsten Fall, wenn der Körper sich um eine raumfeste Achse dreht, die doppelt symmetrisch ist (d. h. beide Symmetrieebenen schneiden sich in der Drehachse), vereinfacht sich der Drallsatz zu „Massenträgheitsmoment mal Drehbeschleunigung = Momentensumme“ in Analogie zu „Masse mal Beschleunigung = Kräftesumme“. Das ist der Eulersche Drehimpulssatz, den Leonhard Euler 1754 veröffentlichte.
Aus dem zweiten newtonschen Gesetz („Kraft ist Masse mal Beschleunigung“) ergibt sich der Schwerpunktsatz
Verwandte und veraltete Einheiten
- Das angloamerikanische Maß- und Gewichtssystem wird in einigen internationalen technischen Bereichen (Luft- und Raumfahrt) noch häufig eingesetzt. 1 Nm entspricht 0,73756215 lbf·ft (Pound-force foot), oder umgekehrt 1 lbf·ft entspricht 1,3558179 Nm.
- Die nicht mehr gültige Einheit kp·m (Kilopond Meter) oder kgf·m (auch m·kg) ist nur noch selten anzutreffen. 1 kp·m entspricht 9,80665 Nm, oder umgekehrt 1 Nm entspricht 0,10197162 kgf·m.
Literatur
- Istvan Szabó: Einführung in die Technische Mechanik, Springer, 1999, ISBN 3540442480
- Peter Gummert, Karl-August Reckling: Mechanik, Vieweg, 1994, ISBN 352828904X
Siehe auch
- Drehmoment und Drall
Wikimedia Foundation.