- Hermann-Mauguin
-
Die Hermann-Mauguin-Symbolik wird zur Beschreibung von Symmetrieelementen und Symmetriegruppen verwendet. Benannt ist sie nach den beiden Kristallographen Carl Hermann und Charles-Victor Mauguin. Ihr Hauptanwendungsgebiet ist die Beschreibung der 32 kristallographischen Punktgruppen und der 230 kristallographischen Raumgruppen. Weiter wird sie auch zur Beschreibung von zweidimensionalen ebenen Gruppen, zwei- und dreidimensionalen subperiodischen Gruppen (Bandornament-, Stab- und Schichtgruppen) und nicht kristallographischen Gruppen verwendet. Normiert ist sie in den International Tables for Crystallography. Neben der Symbolik nach Hermann-Mauguin existiert auch eine Schreibweise nach Arthur Moritz Schönflies, die heute jedoch kaum mehr für den kristallinen Zustand, sondern für die Beschreibung der Symmetrie von Molekülen Anwendung findet. Während es zu jedem Schönflies-Symbol eine entsprechende Hermann-Mauguin-Darstellung gibt, trifft der umgekehrte Fall nicht zu.
Inhaltsverzeichnis
Symbole der Symmetrieelemente
Inversionszentrum
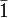 : Inversionszentrum. Vervielfältigung eines Teilchens durch Punktspiegelung. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen.
: Inversionszentrum. Vervielfältigung eines Teilchens durch Punktspiegelung. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen.
Drehachsen
Eine Drehung um
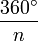 wird durch
wird durch 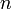 (gesprochen „n-fache Drehung“) dargestellt. Spezialfälle sind
(gesprochen „n-fache Drehung“) dargestellt. Spezialfälle sind 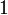 , eine Drehung um 360°, entsprechend der Identität und
, eine Drehung um 360°, entsprechend der Identität und 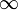 , eine Drehung um einen beliebig kleinen Winkel.
, eine Drehung um einen beliebig kleinen Winkel.In kristallographischen Raum- und Punktgruppen können folgende Drehungen vorkommen.
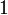 : Die Identität ist Element jeder Gruppe.
: Die Identität ist Element jeder Gruppe.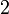 : zweizählige Drehachse, das heißt Drehung um 180°. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen.
: zweizählige Drehachse, das heißt Drehung um 180°. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen.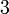 : dreizählige Drehachse, das heißt Drehung um 120°. Es entstehen insgesamt drei symmetrieäquivalente Teilchen.
: dreizählige Drehachse, das heißt Drehung um 120°. Es entstehen insgesamt drei symmetrieäquivalente Teilchen.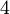 : vierzählige Drehachse, das heißt Drehung um 90°. Es entstehen insgesamt vier symmetrieäquivalente Teilchen.
: vierzählige Drehachse, das heißt Drehung um 90°. Es entstehen insgesamt vier symmetrieäquivalente Teilchen.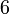 : sechszählige Drehachse, das heißt Drehung um 60°. Es entstehen insgesamt sechs symmetrieäquivalente Teilchen.
: sechszählige Drehachse, das heißt Drehung um 60°. Es entstehen insgesamt sechs symmetrieäquivalente Teilchen.
Spiegelebene
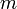 : Spiegelebene. Vervielfältigung eines Teilchens durch Spiegelung an einer Ebene. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen.
: Spiegelebene. Vervielfältigung eines Teilchens durch Spiegelung an einer Ebene. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen.
Gekoppelte Symmetrieoperationen (Drehinversionsachsen)
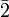 : zweizählige Drehinversionsachse, das heißt Drehung um 180° und anschließende Punktspiegelung. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen. Da diese Operation zum selben Ergebnis wie die Spiegelung an einer Ebene führt, wird diese Symbol nicht verwendet, sondern immer als Spiegelebene
: zweizählige Drehinversionsachse, das heißt Drehung um 180° und anschließende Punktspiegelung. Es entstehen insgesamt zwei symmetrieäquivalente Teilchen. Da diese Operation zum selben Ergebnis wie die Spiegelung an einer Ebene führt, wird diese Symbol nicht verwendet, sondern immer als Spiegelebene 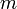 angegeben.
angegeben.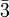 : dreizählige Drehinversionsachse, das heißt Drehung um 120° und anschließende Punktspiegelung. Es entstehen insgesamt sechs symmetrieäquivalente Teilchen.
: dreizählige Drehinversionsachse, das heißt Drehung um 120° und anschließende Punktspiegelung. Es entstehen insgesamt sechs symmetrieäquivalente Teilchen.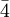 : vierzählige Drehinversionsachse, das heißt Drehung um 90° und anschließende Punktspiegelung. Es entstehen insgesamt vier symmetrieäquivalente Teilchen.
: vierzählige Drehinversionsachse, das heißt Drehung um 90° und anschließende Punktspiegelung. Es entstehen insgesamt vier symmetrieäquivalente Teilchen.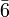 : sechszählige Drehinversionsachse, das heißt Drehung um 60° und anschließende Punktspiegelung. Es entstehen insgesamt sechs symmetrieäquivalente Teilchen.
: sechszählige Drehinversionsachse, das heißt Drehung um 60° und anschließende Punktspiegelung. Es entstehen insgesamt sechs symmetrieäquivalente Teilchen.
Kombinierte Symmetrieoperationen (Drehachsen senkrecht zu Spiegelebenen)
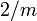 : zweizählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „zwei über m“). Es entstehen insgesamt vier symmetrieäquivalente Teilchen.
: zweizählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „zwei über m“). Es entstehen insgesamt vier symmetrieäquivalente Teilchen.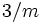 : dreizählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „drei über m“). Es entstehen insgesamt sechs symmetrieäquivalente Teilchen. Da diese Operation zum selben Ergebnis wie die sechszählige Drehinversionsachseachse führt, wird diese Symbol nicht verwendet, sondern immer als sechszählige Drehinversionsachseachse
: dreizählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „drei über m“). Es entstehen insgesamt sechs symmetrieäquivalente Teilchen. Da diese Operation zum selben Ergebnis wie die sechszählige Drehinversionsachseachse führt, wird diese Symbol nicht verwendet, sondern immer als sechszählige Drehinversionsachseachse 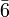 angegeben.
angegeben.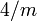 : vierzählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „vier über m“). Es entstehen insgesamt acht symmetrieäquivalente Teilchen.
: vierzählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „vier über m“). Es entstehen insgesamt acht symmetrieäquivalente Teilchen.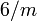 : sechszählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „sechs über m“). Es entstehen insgesamt zwölf symmetrieäquivalente Teilchen.
: sechszählige Drehachse senkrecht zu einer Spiegelebene (gesprochen „sechs über m“). Es entstehen insgesamt zwölf symmetrieäquivalente Teilchen.
Symbole der Punktgruppen
Mit den oben beschriebenen Symbolen lassen sich die 32 Punktgruppen (Kristallklassen) beschreiben, da die Symmetrieoperationen der Kristallklassen keine Translation (siehe Abschnitt zu Raumgruppen) beinhalten.
Im triklinen Kristallsystem gibt es die Punktgruppen
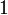 (Abwesenheit von Inversionszentren) und
(Abwesenheit von Inversionszentren) und 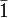 (Anwesenheit von Inversionszentren). Für andere Kristallsysteme werden die Symmetrieoperationen bezüglich drei vorgegebener kristallographischer Richtungen angegeben.
(Anwesenheit von Inversionszentren). Für andere Kristallsysteme werden die Symmetrieoperationen bezüglich drei vorgegebener kristallographischer Richtungen angegeben.Kristallsystem 1. Stelle 2. Stelle 3. Stelle monoklin ![[100]\;](/pictures/dewiki/48/02c52a34062e716c77370cb11d1bfb50.png)
![[010]\;](/pictures/dewiki/53/52b4168967b673cedcfd85291e545368.png)
![[001]\;](/pictures/dewiki/51/30e467bb932745514fcaf54599c339de.png)
orthorhombisch ![[100]\;](/pictures/dewiki/48/02c52a34062e716c77370cb11d1bfb50.png)
![[010]\;](/pictures/dewiki/53/52b4168967b673cedcfd85291e545368.png)
![[001]\;](/pictures/dewiki/51/30e467bb932745514fcaf54599c339de.png)
tetragonal ![[001]\;](/pictures/dewiki/51/30e467bb932745514fcaf54599c339de.png)
![[100]\;](/pictures/dewiki/48/02c52a34062e716c77370cb11d1bfb50.png)
![[110]\;](/pictures/dewiki/56/806d6dff8d677f80b7813a289d85100b.png)
trigonal / hexagonal ![[001]\;](/pictures/dewiki/51/30e467bb932745514fcaf54599c339de.png)
![[100]\;](/pictures/dewiki/48/02c52a34062e716c77370cb11d1bfb50.png)
![[210]\;](/pictures/dewiki/100/d22f5ae960ab4b42b3ef84dff5d70c6d.png)
kubisch ![[100]\;](/pictures/dewiki/48/02c52a34062e716c77370cb11d1bfb50.png)
![[111]\;](/pictures/dewiki/98/bb3bdb508afeff2cccfae4dcafc5aacf.png)
![[110]\;](/pictures/dewiki/56/806d6dff8d677f80b7813a289d85100b.png)
Es werden die Dreh- und Drehinversionsachsen parallel und die Spiegelebenen senkrecht zu diesen Zonen angegeben. Bei trigonalen Punktgruppen ist zu beachten, dass die Zonen bezüglich der hexagonalen Aufstellung des Koordinatensystems angegeben sind. Bei der gekürzten Schreibweise der Hermann-Mauguin-Symbole werden redundante Informationen weggelassen. Statt
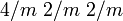 wird zum Beispiel
wird zum Beispiel 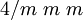 geschrieben.
geschrieben.Symbole der Raumgruppen
Die Bezeichnung für die Raumgruppen funktioniert im Prinzip wie die der Punktgruppen. Zusätzlich wird die Zentrierung des Bravais-Gitters vorangestellt:
- P: Primitiv
- A, B oder C: Flächenzentriert
- F: Allseitig Flächenzentriert
- I: Innenzentriert
- R: Trigonales Gitter mit rhomboedrischer Zentrierung
Es treten außerdem zusätzliche Symbole auf:
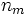 :
: 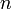 -zählige Schraubung mit Translation um
-zählige Schraubung mit Translation um 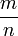 Teile eines Gittervektors.
Teile eines Gittervektors.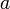 ,
, 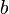 oder
oder  : Gleitspiegelebene mit Translation entlang eines halben Gittervektors.
: Gleitspiegelebene mit Translation entlang eines halben Gittervektors.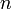 : Gleitspiegelebene mit Translation entlang einer halben Flächendiagonale.
: Gleitspiegelebene mit Translation entlang einer halben Flächendiagonale.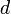 : Gleitspiegelebene mit Translation entlang einer viertel Flächendiagonale.
: Gleitspiegelebene mit Translation entlang einer viertel Flächendiagonale. : Zwei Gleitspiegelungen mit gleicher Gleitspiegelebene und Translation entlang zweier (verschiedener) halber Gittervektoren.
: Zwei Gleitspiegelungen mit gleicher Gleitspiegelebene und Translation entlang zweier (verschiedener) halber Gittervektoren.
Ein Beispiel für eine tetragonale Raumgruppe in gekürzter Schreibweise ist
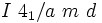 .
.
Wikimedia Foundation.
