Hessematrix

Die Hesse-Matrix (nach Otto Hesse) fasst die partiellen zweiten Ableitungen einer mehrdimensionalen Funktion f(x₁,..x_n), die in die reellen oder komplexen Zahlen abbildet, zusammen:

$\operatorname{H}(f)=\operatorname{H}_f= \left(\frac{\partial^2f}{\partial x_i\partial x_j}\right)= \begin{pmatrix} \frac{\partial^2 f}{\partial x_1\partial x_1}&\frac{\partial^2 f}{\partial x_1\partial x_2}&\cdots&\frac{\partial^2 f}{\partial x_1\partial x_n}\\[,5em] \frac{\partial^2 f}{\partial x_2\partial x_1}&\frac{\partial^2 f}{\partial x_2\partial x_2}&\cdots&\frac{\partial^2 f}{\partial x_2\partial x_n}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial^2 f}{\partial x_n\partial x_1}&\frac{\partial^2 f}{\partial x_n\partial x_2}&\cdots&\frac{\partial^2 f}{\partial x_n\partial x_n} \end{pmatrix}$

Die Hesse-Matrix entspricht dem Transponierten der Ableitung des Gradienten, ist aber bei stetigen zweiten Ableitungen wegen der Vertauschbarkeit der Differentiationsreihenfolge (Satz von Schwarz) symmetrisch, so dass das Transponieren der Matrix keine Änderung bewirkt.

Mit Hilfe der Hesse-Matrix H lässt sich der Charakter der kritischen Punkte einer Abbildung in 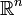$\mathbb R^n$ bestimmen. Dazu bestimmt man für die zuvor ermittelten kritischen Punkte die Definitheit der Hesse-Matrix H. Ist H an einer Stelle positiv definit, so befindet sich dort ein lokales Minimum der Funktion. Ist H dort negativ definit, so handelt es sich um ein lokales Maximum. Ist H indefinit, dann handelt es sich um einen Sattelpunkt der Funktion, d. h., es liegt weder ein Minimum noch ein Maximum vor. Falls H an der untersuchten Stelle nur semidefinit ist, so versagt dieses Kriterium und der Charakter des kritischen Punktes muss auf anderem Wege ermittelt werden. Welcher dieser Fälle vorliegt, kann – wie unter Definitheit beschrieben – z. B. mit Hilfe der Vorzeichen der Eigenwerte von H oder ihrer Hauptminoren entschieden werden.

Anwendungen

Die Hesse-Matrix taucht bei der Approximation einer mehrdimensionalen Funktion in der Taylor-Entwicklung auf. Sie ist unter anderem in Zusammenhang mit der Optimierung von Systemen von Bedeutung, die durch mehrere Parameter beschrieben werden, wie sie beispielsweise in den Wirtschaftswissenschaften, in der Physik, theoretischen Chemie oder in den Ingenieurwissenschaften häufig auftreten.

Siehe auch

• Jacobi-Matrix
• Geränderte Hesse-Matrix