- Hilbert-Transformation
-
Die Hilbert-Transformation ist in der Funktionalanalysis, einem Teilgebiet der Mathematik, eine lineare Integraltransformation. Sie ist nach David Hilbert benannt, welcher sie Anfang des 20. Jahrhunderts bei Arbeiten am Riemann–Hilbert-Problem für holomorphe Funktionen formulierte.
Sie wird im Bereich der Fourier-Transformation und der Fourieranalyse angewendet. Weitere Anwendungsgebiete liegen im Bereich der Signalverarbeitung, bei der sie dazu dient, aus einem reellen Signal ein analytisches Signal bzw. ein monogenes Signal zu bilden.
Inhaltsverzeichnis
Definition
Die Hilbert-Transformation ist für reelle Variablen x und y und für reell- oder komplexwertige Funktionen f und g definiert als:
Dieses Integral hat die Form eines Faltungsintegrals, so dass sich die Hilbert-Transformation mit dem Faltungsoperator * auch in folgender Form schreiben lässt:
Wie bei jeder Transformation existiert auch deren Umkehrung. Die inverse Hilbert-Transformation ist gegeben durch:
Eigenschaften
Einige wesentliche Eigenschaften der Hilbert-Transformation bei reeller Variable t und für reelle oder komplexe Funktionen x bzw. y sind:
- Linearität

- Filterung

Beziehung zur Fourier-Transformation
Insbesondere in der Nachrichtentechnik und deren Signalverarbeitung spielt der Bezug zur Fourier-Transformation eine wesentliche Rolle. Hierfür sind die Transformationspaare in beiden Richtungen von Interesse.
unsymmetrische Normierung Transformation mit der Frequenz Betrachtet sei nun die Faltungsoperation im Zeitbereich, die der Multiplikation im Frequenzbereich entspricht.
Das führt zur Übertragungsfunktion
 .
.
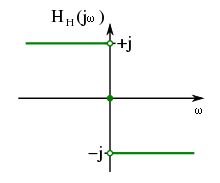
Die Hilbert-Transformation kann in diesem Zusammenhang als eine Phasenverschiebung um π/2 (bzw. +90°) für negative Frequenzen und um −π/2 (bzw. −90°) für positive Frequenzen aufgefasst werden. Nachrichtentechnische Anwendungen liegen im Bereich von Modulationsverfahren, insbesondere der Einseitenbandmodulation als Bestandteil eines analytischen Signals. Die technische Realisierung erfolgt näherungsweise in Form von speziellen Allpassfiltern, die auch als Hilbert-Transformatoren bezeichnet werden.
Diskrete Hilbert-Transformation
Ein bandbegrenztes Signal g(t) limitiert auch die Hilbert-Transformierte von g(t) auf die gleiche Bandbreite. Beträgt die Bandbegrenzung maximal die halbe Abtastfrequenz, kann zufolge des Nyquist-Shannon-Abtasttheorems ohne Informationsverlust eine zeitdiskrete Folge g[k], mit k positiv und ganzzahlig, gebildet werden. Die diskrete Hilbert-Transformation ist dann gegeben als:
mit der Impulsantwort h[k] der zeitdiskreten Hilbert-Transformation:
Die zeitdiskrete Hilbert-Transformation ist nicht kausal – für praktische Implementierungen im Rahmen der digitalen Signalverarbeitung wo diese Form eine Rolle spielt, wird h[k] näherungsweise mittels einer endlichen Länge implementiert. Zu beachten ist, dass die zeitdiskrete Impulsantwort h[k] nicht der abgetasteten, kontinuierlichen Impulsantwort h(t) entspricht.
Kausalitätsbedingung im Frequenzbereich
Durch die Impulsantwort lässt sich ein System vollständig beschreiben. Soll die Bedingung Kausalität erfüllt werden, dann muss die Impulsantwort für die Zeit vor der Anregung den Wert Null aufweisen. Abstrakt lässt sich das über eine Multiplikation mit der Sprungfunktion ausdrücken.
Durch Fouriertransformation lässt sich aus der Impulsantwort die entsprechende Übertragungsfunktion H im Frequenzbereich ermitteln. Das führt schließlich zu einem Faltungsintegral, das der Hilbert-Transformation entspricht.
Daraus folgen die Kausalitätsbedingungen für eine beliebige Übertragungsfunktion:
und
Korrespondenzen
Einige wichtige Korrespondenzen der Hilbert-Transformation sind: (Hinweis: Die Voraussetzungen wie gültiger Wertebereich oder Definitionsbereich wurden der Übersicht wegen weggelassen.)
Signal

Hilbert Transformierte








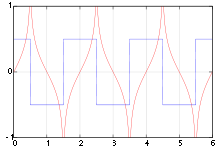
Sinc-Funktion

Rechteck-Funktion
δ(t)
Dirac-Delta-Funktion


Fehlerfunktion erfImplementierung
Für praktische Implementierungen kann die diskrete Hilbert-Transformation einer reellen Zahlenfolge der Länge N mittels der diskreten Fourier-Transformation (DFT) näherungsweise realisiert werden: Zunächst wird die Fourier-Transformierte der Eingabefolge berechnet, danach werden in dem berechneten Spektrum alle Spektralanteile, die für negative Frequenzanteile stehen, auf 0 gesetzt. Abschließend wird mittels der inversen Fouriertransformation (IDFT) die Ausgabefolge berechnet.[1]
- Berechnung der Fouriertransformierten X[i] von der Eingangsfolge mit der Länge N. Auf Effizienzgründen werden dafür FFT-Algorithmen eingesetzt.
- Bildung eines Vektors H[i] der Länge N, der nur die Werte 0, 1 und 2 nach folgender Regel aufweist:
- Wert 1 für den Index i = 1, (N/2)+1
- Wert 2 für den Index i = 2, 3, … , (N/2)
- Wert 0 für den Index i = (N/2)+2, … , N
- Bildung des elementweisen Produktes Y[i] von X[i] mit H[i]
- Berechnung der inversen Fouriertransformierten IDFT von Y[i], um die Ausgangsfolge zu bestimmen.
Alternativ kann die Hilbert-Transformation in Näherung auch mit FIR-Filtern gerader Ordnung in Form eines Allpasses realisiert werden.
Funktionalanalysis
Die Hilbert-Transformation hat als Operator zwischen Funktionenräumen einige Bedeutung. Es ist eine nicht triviale Tatsache, dass die Hilbert-Transformation einen beschränkten Operator
 , für
, für  definiert.
definiert.Die Hilbert-Transformation ist unitär und erfüllt die Gleichung
 , wobei
, wobei  die identische Abbildung ist.
die identische Abbildung ist.Die Hilbert-Transformation ist für
 für
für ![p\in (1,\infty ]](a/b0af6d70bf818fdbcd672310f3d00acd.png) nicht, allerdings für
nicht, allerdings für  schwach beschränkt.
schwach beschränkt.Beziehung zu den Kramers-Kronig-Relationen
Die Kramers-Kronig-Relationen der Physik erhält man mit der formalen Identität (siehe Distribution (Mathematik))
wobei der erste Teil bei der Integration über x den Cauchy-Hauptwert CH von (1/x) und der zweite Teil das π-fache der δ-Funktion δ(x) ergibt.
Die Hilbert-Transformation findet dann Anwendung, wenn eine reelle Funktion von der reellen Achse
 zu einer im darüber liegenden Halbraum holomorphen komplexen Funktion fortgesetzt werden soll.
zu einer im darüber liegenden Halbraum holomorphen komplexen Funktion fortgesetzt werden soll.Literatur
- Karl Dirk Kammeyer: MATLAB in der Nachrichtentechnik. J. Schlembach Fachverlag, 2001, ISBN 3-935340-05-2.
- Bernd Girod,Rudolf Rabenstein,Alexander K. E. Stenger: Einführung in die Systemtheorie: Signale und Systeme in der Elektrotechnik und Informationstechnik. 4. Auflage. Teuber Verlag, Wiesbaden 2007, ISBN 978-3-8351-0176-0.
Einzelnachweise
- ↑ S. Lawrence Marple: Computing the discrete-time analytic signal via FFT, IEEE Transactions on Signal Processing, Ausgabe 47, Nr. 9, September 1999, Seiten 2600-2603
Weblinks
Wikimedia Foundation.










![\mathcal{H} \left\{ g[k] \right\} = h[k] \ast g[k]](3/483ed7100d247a2e6be5a16489fa2131.png)
![h[k]= \frac{1 - \mathrm{cos}(\pi k)}{\pi k} =
\begin{cases}
0, & k \mbox{ gerade},\\
\frac2{\pi k} & k \mbox{ ungerade}
\end{cases}](d/47dbf66a3daac1511f983ba3475ca05a.png)

![H(\mathrm{j}\omega) =
- \mathrm{j} \mathcal{H} \left\{H(f) \right\} =
- \mathrm{j} \cdot \left[ \Re\left(\mathcal{H} \left\{H(f) \right\}\right) +
\mathrm{j} \Im\left(\mathcal{H} \left\{H(f) \right\}\right)\right] =
\Re\left(H(f)\right) + \mathrm{j}\Im\left(H(f)\right)](6/4d68f45415284f77241bbf6650737207.png)


