Diskrete Fourier-Transformation

Die Diskrete Fourier-Transformation oder DFT ist eine Transformation aus dem Bereich der Fourier-Analysis. Sie bildet ein zeitdiskretes, endliches Signal, welches periodisch fortgesetzt wird, auf ein diskretes, periodisches Frequenzspektrum ab, welches auch als Bildbereich bezeichnet wird. Die DFT besitzt zur Signalanalyse große Bedeutung in der digitalen Signalverarbeitung, wo optimierte Varianten in Form der schnellen Fourier-Transformation (englisch Fast Fourier Transformation, FFT) und ihrer Inversen Anwendung finden.

Die DFT wird in der Signalverarbeitung für viele Aufgaben verwendet, so z. B.

• zur Bestimmung der in einem abgetasteten Signal hauptsächlich vorkommenden Frequenzen,
• zur Bestimmung der einzelnen Amplituden zu diesen Frequenzen
• zur Implementierung digitaler Filter mit großen Filterlängen

Mit der inversen DFT (iDFT) kann aus den Frequenzanteilen wiederum das Signal im Zeitbereich rekonstruiert werden. Durch Kopplung von DFT und iDFT kann ein Signal im Frequenzbereich manipuliert werden, wie es beim Equalizer angewendet wird. Die Diskrete Fourier-Transformation ist von der verwandeten Fouriertransformation für zeitdiskrete Signale (englisch Discrete-Time Fourier Transform, DTFT) zu unterscheiden, welche aus zeitdiskreten Signal ein kontinuierliches Frequenzspektrum bildet.

Definition

Die diskrete Fourier-Transformation verarbeitet eine Folge von Zahlen a = (a₀,...,a_{N − 1}), die zum Beispiel als Messwerte aus einer Periode eines periodischen Signals entstanden sind. Die Einträge der Folge werden als Werte a_k = A(z_k) eines Polynoms

$A(z)=\tfrac1N\left(\hat a_0+\hat a_1z+\dots+\hat a_{N-1}z^{N-1}\right)$

mit komplexen Koeffizienten dargestellt. Als Argumente $z_0,z_1,\dots,z_{N-1}$ werden N Punkte auf dem Einheitskreis der komplexen Zahlenebene gewählt, die gleichmäßig verteilt sind, d. h. die N–ten Einheitswurzeln

$z_k=e^{\frac{2\pi \mathrm{i}}{N}k}=\cos(\tfrac{2\pi}{N}k)+\mathrm{i}\,\sin(\tfrac{2\pi}{N}k)$.

Wird nun das Polynom A(z) mit einer gleichmäßig den Einheitskreis umlaufenden Funktion $z(t)=e^{\mathrm{i}2\pi\frac{t-t_0}T}$ verknüpft, so ergibt sich eine zeitkontinuierliche periodische Funktion

$f(t)=A(z(t)) =\tfrac1N\left(\hat a_0+\hat a_1e^{\mathrm{i}2\pi\frac{t-t_0}T}+\hat a_2e^{2\cdot \mathrm{i}2\pi\frac{t-t_0}T} + \dots + \hat a_{N-1}e^{(N-1)\cdot \mathrm{i}2\pi\frac{t-t_0}T}\right) \,$

die zu den Zeiten $t_k=t_0+\tfrac{k}{N}T$ gerade die Funktionswerte a_k annimmt. Die Potenzen von z(t) haben die Gestalt

$z(t)^k=e^{k\cdot \mathrm{i}2\pi\frac{t-t_0}T}=\cos(2k\pi\tfrac{t-t_0}T)+\mathrm{i}\,\sin(2k\pi\tfrac{t-t_0}T)$

und daher die Periode T/k und die Frequenz k/T bzw. die Kreisfrequenz 2kπ / T. Somit ist die Folge der Messwerte durch die Superposition eines konstanten Pegels bei k=0, einer Grundschwingung bei k=1 und Oberschwingungen bei k>1 dargestellt und interpoliert worden.

Diese oben angegebene Interpolationsfunktion ist nicht die einzige, die sich auf diese Art konstruieren lässt. Jede der Funktionen

$\begin{matrix} f(t) =\frac1N&\left(\hat a_0+\hat a_1e^{\mathrm{i}2\pi\frac{t-t_0}T}+\hat a_2e^{2\cdot \mathrm{i}2\pi\frac{t-t_0}T}+\dots+\hat a_{M-1}e^{(M-1)\cdot \mathrm{i}2\pi\frac{t-t_0}T}\right.\\ &\left.+ \hat a_{M}e^{(M-N)\cdot \mathrm{i}2\pi\frac{t-t_0}T}+\dots+\hat a_{N-1}e^{(N-1-N)\cdot \mathrm{i}2\pi\frac{t-t_0}T}\right) \end{matrix}$

hat diese Interpolationseigenschaft.

DFT und iDFT für einen komplexen Vektor

Die diskrete Fourier-Transformierte $\hat a=(\hat a_0,...,\hat a_{N-1})\in\Bbb C^N$ eines komplexen Vektors $a=(a_0,...,a_{N-1})\in\Bbb C^N$ hat die Koeffizienten

$\hat a_k = \sum_{j=0}^{N-1} e^{-2\pi \mathrm{i}\cdot\frac{jk}{N}}\cdot a_j$     für   $k=0,\dots,N-1$.

Dabei nennt man die $\hat a_k$ auch Fourierkoeffizienten oder Fourierkomponenten.

Die inverse DFT (iDFT) a von $\hat a\in\Bbb C^N$ hat die Koeffizienten

$a_k=\frac 1 N \sum_{j=0}^{N-1} e^{2\pi \mathrm{i}\cdot\frac{jk}{N}}\cdot \hat a_j$     für   $k=0,\dots,N-1 \,$.

Sonderfall: DFT für einen reellen Vektor

Wie bei der Fourier-Transformation gelten auch für die DFT gewisse Symmetriegesetze. So wird ein reelles Signal im Zeitraum zu einem hermiteschen Signal ($g(-\vec x)=\overline{g(\vec x)}$) im Frequenzraum:

$\hat a_{N-k}=\overline{\hat a_k} \,$

Dies bedeutet, dass im Frequenzraum nur N / 2 unabhängige komplexe Koeffizienten $\hat a_k$ vorliegen. Diese Tatsache kann bei der Implementierung der DFT ausgenutzt werden, wenn bekannt ist, dass das Eingangssignal rein reell ist. Für die Darstellung des Ergebnisses sind dann keine N (wie bei der vollen DFT), sondern nur N / 2 komplexe Zahlen nötig. Die anderen N / 2 komplexen Zahlen können durch elementare Rechnung rekonstruiert werden (siehe Formel oben). Die hermitesche Symmetrie bezieht sich auf das mittlere Element k = N / 2 des Signals $\hat a_k$.

Beweis: Wegen der Eulerschen Identität e^2πi = 1 und wegen $\overline{e^{\mathrm{i}\phi}}=e^{-\mathrm{i}\phi}$ gilt im reellen Fall $a\in\R^N$:

$\hat a_{N-k} =\sum_{j=0}^{N-1}e^{-2\pi \mathrm{i}\cdot\frac{Nj}{N}}e^{2\pi \mathrm{i}\cdot\frac{jk}{N}}\cdot a_j =\sum_{j=0}^{N-1}\overline{e^{-2\pi \mathrm{i}\cdot\frac{jk}{N}}\cdot a_j} =\overline{\hat a_k} \,$

Umgekehrt gilt entsprechend: Erfüllt $\hat a\in\C^N$ die Bedingung $a_{N-k}=\overline{a_k}$ für alle $k=0,\dots,N-1$, so ist die inverse DFT ein reeller Vektor $a\in\R^N$.

Verallgemeinerung: Mathematische Definition der DFT

In der Mathematik wird die diskrete Fouriertransformation in einem sehr allgemeinen Kontext betrachtet. Sie findet unter anderem in der Computer-Algebra bei einer Vielzahl von effizienten Algorithmen zur exakten Arithmetik Anwendung, so zum Beispiel bei der schnellen Multiplikation ganzer Zahlen mit dem Schönhage-Strassen-Algorithmus.

Sei R ein kommutativer unitärer Ring, in dem die Zahl N (das ist die N-fache Summe der 1) eine Einheit ist. Des Weiteren gebe es in R eine primitive N-te Einheitswurzel w. Zu einem „Vektor“ $a=(a_0,\dots,a_{N-1})\in R^N$ ist dann die diskrete Fouriertransformierte $\hat a$ durch

$\hat a_k = \sum_{j=0}^{N-1} w^{\,j\cdot k}\cdot a_j$     für   $k=0,\dots,N-1 \,$

erklärt. Unter den getroffenen Voraussetzungen existiert damit zu $\hat a\in R^N$ auch die diskrete inverse Fouriertransformierte a mit den Koeffizienten

$a_k = {1\over N}\sum_{j=0}^{N-1} w^{-j\cdot k}\cdot \hat a_j$     für  $k=0,\dots,N-1 \,$.

Im überaus wichtigen Spezialfall $R=\Bbb C$ wird für die DFT üblicherweise die N-te Einheitswurzel $\exp\left(2\pi\,\mathrm{i}/N\right)$ benutzt. Dies ergibt die Formel im ersten Abschnitt.

Mehrdimensionale DFT

Die DFT kann leicht auf mehrdimensionale Signale erweitert werden. Sie wird dann je einmal auf alle Koordinatenrichtungen angewendet. Im wichtigen Spezialfall von zwei Dimensionen (Bildverarbeitung) gilt etwa:

$\hat a_{k,l} = \sum_{m=0}^{M-1}\sum_{n=0}^{N-1}a_{m,n}\cdot \mathrm{e}^{-2\pi \mathrm{i}\cdot\frac{mk}{M}} \mathrm{e}^{-2\pi \mathrm{i}\cdot\frac{nl}{N}} \,$

    für   $k=0,\dots,M-1$ und $l=0,\dots,N-1$

Die Rücktransformation lautet entsprechend:

$a_{m,n} = \frac{1}{MN} \sum_{k=0}^{M-1}\sum_{l=0}^{N-1}\hat a_{k,l}\cdot e^{2\pi \mathrm{i}\cdot\frac{mk}{M}} e^{2\pi \mathrm{i}\cdot\frac{nl}{N}} \,$

    für   $m=0,\dots,M-1$ und $n=0,\dots,N-1$

Verschiebung und Skalierung in Zeit und Frequenz

In den Berechnungsformeln von DFT und iDFT kann die Summation (Indexvariable j oben) statt über $0,\dots,N-1$ ebenso auch über einen verschobenen Bereich $k,\dots,N-1+k$ laufen, wenn der Vektor $\textstyle a=(a_0,\ldots,a_{N-1})$ periodisch auf alle ganzzahligen Indizes fortgesetzt wird, denn es gilt $\textstyle w^{N+k} = w^k$. Wir können also die Summationsgrenzen beliebig verschieben, solange ein Segment der Länge N in den ganzen Zahlen überstrichen wird.

Wenden wir uns nun wieder dem komplexen Fall zu. In praktischen Anwendungen möchte man die Indizes mit einer äquidistanten Folge von Zeitpunkten verbinden,

$\displaystyle t_n:=nT$, n=1-M,…,N-M,

die ebenfalls die Länge N hat. Auch ist es wünschenswert, den berechneten Koeffizienten Frequenzen zuzuordnen, die um 0 zentriert sind,

$\displaystyle \omega_n:=2\pi\frac{n}{NT}$, n=1-K,…, N-K,

K in der Nähe von N/2.

Eine zu den gewählten Zeitpunkten „gemessene“ Funktion f ergibt den Beobachtungsvektor $\textstyle x\in\Bbb C^N$ mit den Koeffizienten $\textstyle x_n=f(t_n)$, dessen DFT $\textstyle y_n=\hat f(\omega_n)=F(\omega_n)$ in der Fourier-Analyse betrachtet wird. Dann ist

$F(\omega_n)=\sum_{k=1-M}^{N-M}e^{-2\pi \mathrm{i}\frac{nkT}{NT}}x_k =\sum_{k=1-M}^{N-M}e^{-\mathrm{i}\,\omega_n\cdot t_k}f(t_k) \,$

und

$f(t_n)=x_n=\frac1N \sum_{k=1-K}^{N-K}e^{2\pi \mathrm{i}\frac{nkT}{NT}}y_k =\frac1N \sum_{k=1-K}^{N-K}e^{\mathrm{i}\omega_k\cdot t_n}F(\omega_k) \,$.

Beispiele

Die Fourier-Transformation transformiert eine Funktion f(t) nach g(ν)* von einer Zeitdarstellung t in den reziproken Frequenzraum ν:=1/t. Dies gilt auch für Ortsfunktionen, die auf ein (1D), zwei (2D) oder mehr Raumrichtungen definiert sind. Diese werden durch die Fouriertransformation, nacheinander in jeder Richtung, in Raumfrequenzen überführt. Beugungserscheinungen in der Optik oder Röntgenanalyse können unmittelbar als die Intensitätsverteilung einer Fouriertransformierten interpretiert werden. Die Phasenbeziehung geht bei der Fotografie normalerweise verloren. Lediglich bei der Holographie wird die Phasenbeziehung durch eine Überlagerung mit einem Referenzstrahl mit aufgezeichnet.

Einfache Blenden

Berechnete 2D Fourier-Transformationen. Links Ausgangsbild, rechts Intensitätsverteilung der Fourier-Transformation.

Berechnete 2D Fourier-Transformationen. Links Ausgangsbild, rechts Intensitätsverteilung der Fourier-Transformation.

Die Bilder rechts veranschaulichen zweidimensionale Fourier-Transformationen (2D FFT) an geometrischen Mustern, gerechnet für Quadrate der diskreten Größe von a x a Pixeln. Das Bild oben links zeigt einen Spalt der Größe e x f Pixel, daneben die Intensitätsverteilung des Beugungsbildes. Die Ortsvariable r wird überführt in reziproke komplexe Werte r*. Bei den gewählten Größen wird ein Pixel auf den reziproken Wert von 1/a reziproken Pixeln überführt. Die Breite des Spalts von e Pixeln erscheint im Reziprok-Raum als Wert der Größe r*=a/e, die Höhe r*=a/f, mit harmonischen Frequenzen höherer Ordnung. Die berechneten Beugungsbilder geben die Intensitätsverteilungen der komplexen Größe r* wieder. Dass sie nur die Hälfte der Bildinformation tragen, erkennt man an ihrer Rotationssymmetrie.

Die periodischen Peaks entsprechen den Ortsfrequenzen höherer Ordnung eines Rechtecksignals. Ähnliche Beispiele finden sich unter den Stichworten Fourier-Analyse, Fourier-Transformation, oder Beugungsscheibchen.

Im zweiten Teilbild wird ein regelmäßiges Sechseck gebeugt. Wieder erscheint die Größe der Figur als Periode im Beugungsbild rechts. Die 6-zählige Symmetrie ist deutlich zu erkennen. Eine Verschiebung des Ausgangsbildes – im Gegensatz zu einer Drehung – würde sich nur in der Phasenbeziehung auswirken, die in der gewählten Darstellung als Intensitätsverteilung nicht zu erkennen ist.

Das untere Teilbild zeigt rechts das gerechnete Beugungsmuster eines Dreiecks. Die 6-zählige Symmetrie ist nur vorgetäuscht, was an der fehlenden Modulation der Beugungssterne zu erkennen ist.

Die zweite Bildserie vergleicht die Beugung zweier Kreisöffnungen. Ein großer Kreis erzeugt ein kleines Beugungsmuster, und umgekehrt. Bei einem Fernrohr begrenzt die Lichtbeugung an der Linsenöffnung die Auflösung. Je größer der Durchmesser ist, desto kleiner ist das Beugungsbild eines Sterns, desto besser können nahe beieinander liegende Sterne voneinander unterschieden werden.

Das untere Bild ist ein Beispiel für eine Beugung an einer Kreis-Struktur ohne scharfe Begrenzung. Bei einer sinusförmigen Intensitätsabnahme am Rad treten keine Beugungen höherer Ordnung auf (siehe auch Zonenplatte).

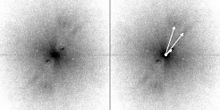
Bild mit periodischen Strukturen

SAR-Bild des indischen Ozeans

FFT des SAR-Bildes

Die Aufnahme links zeigt eine SAR-Aufnahme des indischen Ozeans mit Wasserwellen unterschiedlicher Wellenlänge. Die internen Wellen oben rechts haben eine Wellenlänge von ca. 500 m. Die durch Wind erzeugten Oberflächenwellen sind in der verkleinerten Darstellung nicht erkennbar. Im gerechneten Beugungsbild geben die beiden dunklen Reflexe (siehe kurzer Pfeil) sowohl die Richtung, als auch die mittlere Wellenlänge der regelmäßigen langperiodischen Wasserwellen an. Die Wellenlängen der Oberflächenwellen variieren stärker, weshalb sie keine scharfen Reflexe liefern. Es liegen zwei ausgezeichnete Richtungen für die Wellenausbreitung vor, die im Direktbild nur undeutlich zu sehen sind. Die Wellenlängen betragen ca. 150 m (langer Pfeil) und 160 m (etwas kürzerer Pfeil).

Mathematische Grundlage

Die in der diskreten Fouriertransformation auftretenden komplexen Zahlen

$e^{i\,2\pi \frac{n}N} \,$

sind N-te Einheitswurzeln, d. h. sie sind Lösungen der Gleichung q^N − 1 = 0. Sei $q:=e^{2\pi\,i/N}$ die „kleinste“, also primitive Wurzel im ersten Quadranten. Diese genügt folgender Identität geometrischer Summen von Einheitswurzeln:

$\displaystyle \sum_{k=0}^{N-1} q^{nk}=N\delta_{0,n} \qquad\text{mit } n=0,\ldots,N-1$

denn: $\displaystyle \sum_{k=0}^{N-1} x^k=\frac{x^N-1}{x-1} \,$ für $x\ne1$.

Dieses ist der „tiefe Grund“, weshalb die inverse DFT funktioniert.

Definieren wir in $\mathbb C^N$ die Vektoren $f_n:=(e^{i2\pi\frac{nk}N})_{k=0,\dots,N-1}$, n=0,...,N-1, so bilden diese eine orthonormale Basis zum Skalarprodukt

$\langle x,y\rangle = \frac1N\sum_{k=0}^{N-1}x_k\bar y_k \,$.

Es gilt

$\langle f_n,f_m\rangle = \frac1N\sum_{k=0}^{N-1}e^{i2\pi\frac{(n-m)k}N}=\delta_{n,m}=\begin{cases}1&n=m\\0&n\ne m\end{cases} \,$.

Jeder Vektor $x=(x_0,\dots,x_{N-1})\in\mathbb C^N$ kann in der Orthonormalbasis dargestellt werden:

$\displaystyle x=\sum_{n=0}^{N-1} \langle x,f_n \rangle \cdot f_n \,$

Die Koeffizienten $\langle x,f_n\rangle$ heißen (auch allgemein bei beliebigem Orthonormalsystem) Fourier-Koeffizienten, die DFT ordnet also einem Vektor x bis auf eine additive Konstante den Vektor X=DFT(x) der Fourier-Koeffizienten zu.

Ist Y=DFT(y) mit einem weiteren Vektor $y=(y_0,\dots,y_{N-1})\in\mathbb C^N$, so gilt die Parsevalsche Gleichung für Fourier-Koeffizienten:

$\langle x,y\rangle=\sum_{n=0}^{N-1}\langle x,f_n\rangle\langle f_n,y\rangle=\sum_{n=0}^{N-1}X_n\bar Y_n \,$

Interpretationen der DFT

Diskretisierung der Fourier-Transformation

Die Fourier-Transformation erlaubt es, sich Funktionen mit reellem Argument (und diversen Einschränkungen wie: Integrabilität, Abfall im Unendlichen) aus Schwingungen zusammengesetzt zu denken:

$f(t)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^\infty \hat f(\omega) e^{i \omega t} \,d \omega \,$.

Eine wichtige Erkenntnis der Fourier-Theorie ist, dass die Amplitude $\hat f(\omega)$ sich ähnlich bestimmen lässt zu

$\hat f(\omega)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^\infty f(t) e^{-i \omega t} \,d t \,$

Wählen wir einen Radius R so groß, dass außerhalb des Intervalls [-R,R] nur noch ein unwesentlicher Teil von f liegt, ist f außerdem stetig und eine Zahl N so groß gewählt, dass T:=R/N klein genug ist, um f sinnvoll singulär, d. h. durch Funktionswerte f(kT), abzutasten, so kann das Fourier-Integral in der Transformationsformel sinnvoll durch eine Summe ersetzt werden:

$\hat f(\omega)\approx F(\omega)=\frac{1}{\sqrt{2 \pi}} \sum_{k=-N}^N e^{-i \omega kT}f(kT) \,T \,$.

Das entspricht, bis auf einen konstanten Faktor $T/\sqrt{2 \pi}$, der Berechnungsformel der DFT. Der Vektor x=( f(-NT), ... ,f(NT) ) hat 2N+1 Elemente. Wir wissen bereits, dass es ausreicht, die Frequenzkoeffizienten für die 2N+1 Frequenzen $\omega_n:=2\pi\cdot \frac{n}{(2N+1)T}$, n=-N,...,-1,0,1,...,N, zu bestimmen, um die Funktionswerte im Vektor x zu rekonstruieren. Mit der notwendigen Anpassung der Konstanten in der iDFT erhalten wir

$f(nT)=\frac{1}{\sqrt{2 \pi}}\sum_{k=-N}^N e^{i \omega_k nT}F(\omega_k)\,\frac{2\pi}{(2N+1)T} \,$

Der Diskretisierungsabstand im Frequenzbereich ist proportional zu 1/R, also nach Voraussetzung ebenfalls klein, so dass diese Berechnung der Diskretisierung der inversen Fourier-Transformation entspricht.

Beim Übergang von der Fourier-Transformation zur DFT sind also folgende Veränderungen zu bemerken:

• Das Signal liegt zu diskreten, äquidistanten Zeitpunkten vor (T: Abstand zweier aufeinanderfolgender Zeitpunkte), 0 ist einer dieser Zeitpunkte.
• Das Signal hat eine endliche Länge (2N+1: Anzahl der Werte), welche als Werte innerhalb eines großen Intervalls [-NT,NT] interpretiert werden.
• Die Integrale bei der Berechnung der Fourier-Koeffizienten werden bei der DFT zu Summen.
• Das Spektrum wird nur für eine endliche Anzahl von (Kreis-)Frequenzen berechnet (ω = (2 π)·n/((2N+1)·T); n = -N,…,-1,0, 1, 2,…,N) und ist periodisch in der Frequenz, wobei die Periode (2 π)/T nach Voraussetzung (T klein) sehr groß ist.

Diskretisierung von Fourier-Reihen

Jede periodische Funktion mit reellem Argument (und wieder Einschränkungen wie: Integrabilität, keine Polstellen) und Periode L kann als Funktionenreihe mit Sinusoiden, die Bruchteile von L als Periode haben, dargestellt werden (so genannte Fourier-Reihen):

$f(t)=\sum_{n\in\mathbb Z} c_n(f)e^{\mathrm{i}\cdot \omega_nt} \quad \text{mit} \quad \omega_n=\frac{2\pi n}{L}$

Brechen wir die Reihenentwicklung bei großen Grenzen 1-M unten und N-M oben ab, so erhalten wir mit T:=L/N

$f(t_k)=f(kT)\approx \sum_{n=1-M}^{N-M} c_n(f)e^{2\pi \mathrm{i}\cdot \frac{nk}{N}} \,$

, d. h. wir erhalten eine Form der inversen DFT. Damit können die Koeffizienten mittels DFT approximiert werden zu

$c_n(f)\approx\frac{1}{L}\sum_{k=0}^{N-1} f(kT)e^{-\mathrm{i}\cdot \frac{2\pi nk}{N}}\cdot \frac{L}{N}=\frac{1}{L}\sum_{k=0}^{N-1} f(t_k)e^{-\mathrm{i}\cdot \frac{2\pi n}{L}t_k}\cdot T \,$

Im Grenzfall eines unendlich großen N ergeben sich die bekannten Koeffizientenintegrale der Fourier-Reihen:

$c_n(f)=\frac{1}{L}\int_0^L f(t)e^{-\mathrm{i}\cdot \frac{2\pi n}{L}t}\,d t \,$

Eigenschaften

Spektrum abgetasteter Funktionen

Abb.1: Betrag und Phase des Spektrums eines abgetasteten Signals

Die diskrete Fourier-Transformation besitzt ein periodisches Spektrum, es wiederholt sich mit der Abtastfrequenz und ist symmetrisch zur Abtastfrequenz. Es gilt:

$F\left(\omega+\frac{2 \pi}{T} m\right)= C\sum_{k = 0}^{N - 1} f(kT) e^{-\mathrm{i} \omega kT}e^{-\mathrm{i} \frac{2 \pi}{T}mkT}= F(\omega) \,$

(Denn für natürliche Zahlen m und k gilt: e^{-i2π m k}=1)

$F\left(\frac{2 \pi}{T}-\omega\right)= C\sum_{k = 0}^{N - 1} f(kT) e^{-\mathrm{i} \frac{2\pi}{T} kT} e^{+\mathrm{i} \omega kT}= F^{*}(\omega) \,$

Enthält das abgetastete Signal Frequenzanteile oberhalb der halben Abtastfrequenz, überlappen sich die Spektren des ursprünglichen Signals mit den an der Abtastfrequenz gespiegelten Signalanteilen, und es kommt zum Alias-Effekt.

Alias-Effekt

Siehe auch Hauptartikel: Alias-Effekt

In der Regel entsteht das zeitdiskrete Signal durch Diskretisierung eines kontinuierlichen Signals. Die durch die DFT entstehenden Spektren sind nur dann mit den Spektren des zugrundeliegenden kontinuierlichen Signals identisch, wenn bei der Abtastung das Abtasttheorem (sampling-theorem) nicht verletzt wurde. Für Signale im Basisband muss gelten, dass die Abtastfrequenz mehr als doppelt so groß (Nyquist-Frequenz) sein muss wie die maximal auftretende Frequenz. Bei Verletzung des Abtasttheorems tritt eine Verfälschung des Originalsignals auf (Aliasing im Zeitbereich). Eine Möglichkeit des Anti-Aliasing ist die Bandbegrenzung des Signals am Eingang des Systems, um diesen Effekt zu vermeiden.

DFT einer zeitbegrenzten Funktion

Für periodische Funktionen ergibt sich (analog zur kontinuierlichen Fourier-Transformation) ein Linienspektrum mit einem Frequenzlinienabstand von 1/Periodenlänge.

Abb. 2: Fourier-Transformierte eines Rechteck-Fensters

Eine zeitbegrenzte diskrete Funktion g(kT) kann man aus einer periodischen diskreten Funktion f(kT) ableiten, indem man über ein Zeitfenster w(t) genau eine Periode herausschneidet.

$g(kT) = f(kT) \cdot w(t) \,$

Da bei der Fourier-Transformation eine Multiplikation von Funktionen im Zeitbereich einer Faltung der Fourier-Transformierten im Frequenzbereich entspricht, ergibt sich die DFT der zeitbegrenzten Funktion G(ω) durch die Faltung der DFT der periodischen Funktion F(ω) mit der Fourier-Transformierten des Zeitfensters W(ω).

$G(\omega) = F(\omega) \star W(\omega) \,$

Abb.3: Zusammensetzung des Spektrums einer zeitbegrenzten Funktion

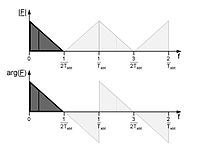
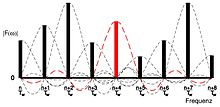
Als Ergebnis erhält man ein Linienspektrum, das durch die Fourier-Transformierte des Zeitfensters verschmiert ist. In Abb.3 rechts gestrichelt dargestellt ist der Einfluss des Zeitfensters auf die DFT der periodischen Funktion (dicke Linien). Durch die Zeitbegrenzung kommen Frequenzanteile zwischen den analysierten Frequenzlinien hinzu.

Durch den Übergang von einer periodischen Funktion auf eine zeitbegrenzte Funktion muss nicht das Rechenverfahren zur Bestimmung des Spektrums verändert werden. Es werden weiterhin diskrete Frequenzlinien berechnet, als ob eine periodische Funktion dahinterstände. Als Effekt des Zeitfensters steht nun jede berechnete Frequenzlinie stellvertretend für einen ganzen Frequenzbereich, nämlich dem Frequenzbereich der durch die Fourier-Transformierte des Zeitfensters hinzugekommen ist. Dieses Verhalten bezeichnet man auch als Leck-Effekt.

Leck-Effekt (Leakage effect)

Siehe auch Hauptartikel: Leck-Effekt

Aufgrund der zeitlichen Begrenzung des Signals kann es dazu kommen, dass das Eingangssignal abgeschnitten wird. Ein abgeschnittenes Eingangssignal kann nur dann korrekt mit der DFT transformiert werden, wenn es periodisch fortsetzbar ist. Falls das Signal nicht periodisch fortsetzbar ist, enthält es Frequenzen, die nicht zu den von der DFT berechneten diskreten Frequenzen gehören. Die DFT „nähert“ diese Frequenzen durch die benachbarten Frequenzen an, dabei wird die Energie auf diese Frequenzen verteilt. Dies wird als Leck-Effekt (engl. Leakage-Effect) bezeichnet.

Die zeitliche Begrenzung kommt einer Multiplikation mit einer Rechteckfunktion gleich und bedeutet im Frequenzbereich eine Faltung mit sin(x)/x (Si-Funktion: Spektrum eines Rechtecks). Dies ist eine andere Betrachtungsweise um den Leck-Effekt zu erklären. Das gilt natürlich auch im Falle anderer Fensterfunktionen. (Hamming, von Hann, Gauss etc.). Somit ist das Spektrum der Fensterfunktion (bzw. die Breite des Spektrums) ausschlaggebend für das Leck. Die Amplitudengenauigkeit ist das andere Kriterium einer Fensterfunktion.

Gleitende DFT als Bandfilterbank

Eine DFT einer zeitbegrenzten Funktion kann man auch als Bandfilterbank ansehen.

• Die Mittenfrequenzen dieser Bandfilter entsprechen den Frequenzlinien der Funktion, die entsteht, wenn man den betrachteten Zeitabschnitt periodisch wiederholt (Vielfache von 1/Fensterbreite).
• Die Breite und Flankensteilheit der Bandfilter wird durch die Fourier-Transformierten des Zeitfensters bestimmt.

(siehe Abb.3)

Durch die Wahl einer geeigneten Zeitfenster-Funktion kann man die Eigenschaften der Bandfilter verändern.

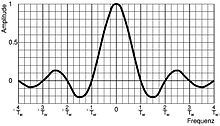
• Bei einem Rechteck-förmigen Zeitfenster mit Unstetigkeits-Stellen an den Fenster-Grenzen werden Frequenzen außerhalb des Übertragungs-Bereichs des Bandfilters mit 1/Frequenz abgeschwächt; man erzielt Flankensteilheiten von 6 dB/Oktave (siehe Abb.2)
• Ist die Fenster-Funktion stetig, werden Frequenzen außerhalb des Übertragungs-Bereichs des Bandfilters mit 1/Frequenz² abgeschwächt; man erzielt Flankensteilheiten von 12 dB/Oktave
• Ist die 1.Ableitung der Fenster-Funktion stetig, werden Frequenzen außerhalb des Übertragungs-Bereichs des Bandfilters mit 1/Frequenz³ abgeschwächt; die Flankensteilheit beträgt 18 dB/Oktave
• usw.

Bestimmt man die Fourier-Transformierte von jeweils aufeinander folgenden Zeitabschnitten, erhält man die gleitende Fourier-Transformation. Mit der Analyse eines neuen Zeitabschnitts erhält man dann neue Abtastwerte für den Zeitverlauf der Spektrallinien (das heißt den Zeitverlauf der Signale an den Ausgängen der „Bandfilter“).

Unschärfe-Relation der gleitenden DFT

Zeit- und Frequenz-Auflösung der gleitenden DFT können nicht unabhängig voneinander gewählt werden.

• Will man Signale mit hoher Frequenzauflösung analysieren, muss man die Zeitfenster sehr groß machen, man erhält eine geringe Zeitauflösung.
• Benötigt man eine hohe Zeitauflösung, muss man die Breite der Zeitfenster sehr kurz machen, dann kann man aber nur wenige Frequenzlinien bestimmen.
• Es gilt: Frequenz-Auflösung ≈ 1/Zeitfensterbreite (wird eine Frequenzauflösung von 1kHz gewünscht muss das Zeitfenster mindestens 1ms lang sein).

FFT

Für Blocklängen N, die sich als Potenz von 2 darstellen lassen, kann die Berechnung mit dem Algorithmus der schnellen Fourier-Transformation (FFT) erfolgen. Allgemein gilt: Kann die Blocklänge faktorisiert werden, N=KM, so gibt es eine Zerlegung der DFT der Länge N in ein Produkt von DFTs der Längen K und M sowie zweier einfacher Matrizen.

Goertzel-Algorithmus

Für beliebige Blocklängen N und zur Bestimmung einer einzigen oder einiger weniger spektraler Komponenten kann auch der Goertzel-Algorithmus verwendet werden. Der Vorteil besteht in einer sehr effizienten Implementierung in Computersystemen, da die Berechnung pro Spektralkomponente nur eine komplexe Multiplikation und zwei komplexe Additionen umfasst.

Anwendungen

• Berechnung der Fourier-Transformierten eines Signals.
• Signalanalyse.
• Schwingungsanalyse und Modalanalyse.
• Bearbeitung von Signalen.
• Berechnung von Korrelationen.
• Berechnung von Polynomprodukten in O(n*Log(n))

Bei der Berechnung von Oberflächenwellenfiltern (= OFW-Filter = SAW-Filter = surface acoustic wave - filter) wird die invers - Fouriertransformierte der Übertragungsfunktion benötigt (stellt die Impulsantwort dar). Diese Aufgabe wird von Rechnern übernommen.

Siehe auch

• Faltung
• Gabor-Transformation
• Laplace-Transformation
• Diskrete Kosinustransformation
• Wavelet-Transformation
• Fensterung
• Fourierreihe
• Short-Time-Fourier-Transformation