Homoskedastie

Homoskedastizität

Heteroskedastizität

Heteroskedastizität

Heteroskedastizität (auch (Residuen)-Varianzheterogenität) bedeutet in der Statistik unterschiedliche Streuung innerhalb einer Datenmessung. Wenn die Varianz der Residuen (und somit die Varianz der erklärten Variablen selbst) für alle Ausprägungen der anderen (Prädiktor-) Variablen nicht signifikant unterschiedlich sind, liegt Homoskedastizität ((Residuen-)Varianzhomogenität) vor. Der Begriff spielt insbesondere in der Ökonometrie und der empirischen Forschung eine wichtige Rolle.

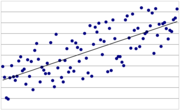
Häufig werden in der Statistik Methoden angewendet, bei denen mehrere gleichartige Merkmale eine Rolle spielen. Beispielsweise hat man in der Regressionsanalyse eine Menge von Datenpunkten gegeben, in die eine Gerade möglichst passgenau eingelegt wird. Die Abweichungen der Datenpunkte von der Geraden werden Störterme oder Residuen genannt und sind wahrscheinlichkeitstheoretisch jeweils Zufallsvariablen. Haben diese Störterme alle die gleiche Varianz, liegt Homoskedastizität vor. Wenn diese Störterme allerdings nicht die gleiche Varianz aufweisen, führt die einfache Kleinstquadratmethode nicht zu effizienten Schätzwerten für die Regressionskoeffizienten. Dies bedeutet, dass diese Schätzwerte nicht die kleinstmögliche Varianz aufweisen. Außerdem ist dann eine naive Anwendung des t-Testes nicht möglich; die t-Werte sind nicht mehr brauchbar. Abhilfe schafft in vielen Fällen eine geeignete Datennormalisierung: Herrscht Heteroskedastizität, kann es durchaus sinnvoll sein, die Daten mittels Anwendung des Logarithmus oder der Quadratwurzel zu transformieren um Homoskedastizität zu erreichen. Diese führt dann zur korrekten Verwendung des Gauss-Markov-Theorems.

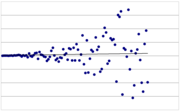
Beispiel: Ein typisches Beispiel für Heteroskedastizität ist, wenn bei einer Zeitreihe die Abweichungen von der Trendgeraden mit Fortlauf der Zeit steigen (z. B. für die Treffgenauigkeit bei der Wettervorhersage: je weiter in der Zukunft, desto unwahrscheinlicher ist eine genaue Prognose). Allerdings können auch in Zeitreihen ohne konstante Varianz bestimmte charakteristische Auffälligkeiten wie z. B. Volatilitätscluster beobachtet werden. Deshalb wurde im Rahmen von Volatilitätsmodellen versucht, dem Verlauf der Varianz eine systematische Erklärung zu Grunde zu legen.

Bekannte Verfahren, um die Nullhypothese „Homoskedastizität“ zu überprüfen, sind der Goldfeld-Quandt-Test, der White-Test, der Glejser-Test und der Breusch-Pagan-Test (siehe englische Wikipedia: Breusch-Pagan statistic).