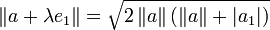Householder-Spiegelung

In der Mathematik beschreibt die Householdertransformation die Spiegelung eines Vektors an der Hyperebene durch Null in einem euklidischen Raum. Im dreidimensionalen Raum ist sie eine lineare Abbildung, die eine Spiegelung an einer Ebene (durch den Ursprung) beschreibt.

Die Householdertransformation wurde 1958 durch den amerikanischen Mathematiker Alston Scott Householder eingeführt.

Definition und Eigenschaften

Die Spiegel-Hyperebene kann durch einen Einheitsvektor v (einen Vektor mit der Länge 1), der orthogonal zur Hyperebene ist, definiert werden.

Wenn v als Spalteneinheitsvektor gegeben und I die Einheitsmatrix ist, dann ist die oben beschriebene lineare Abbildung durch die folgende Householder-Matrix gegeben (v^T bezeichnet die Transponierte des Vektors v):

S_v = I − 2vv^T

Ist v nicht normiert, so lautet die passende Formel:

$S_v = I - \frac {2} {v^T v} v v^T$

Spiegelungsmatrizen gab es selbstverständlich schon lange vorher und in der reinen Mathematik ist der Begriff Householder-Matrix für eine Spiegelungsmatrix eher unbekannt.

Diese Householdermatrix ist nützlich, wenn man eine beliebige Matrix (auch mit linear abhängigen Spalten) mit Hilfe einer orthonormalen Matrix darstellen will. Hat die Matrix linear unabhängige Spalten, so ist sie als QR-Zerlegung in der Form A = QR darstellbar, wobei Q orthonormale Spalten hat. In R ist gespeichert, wie sich die Spalten von A durch die von Q darstellen lassen. Hat A nun linear abhängige Spalten, so kann man A trotzdem Spalte für Spalte mit der Householdermatrix transformieren.

Die Householder-Matrix hat folgende Eigenschaften:

• sie ist symmetrisch: S = S^T
• sie ist orthogonal: S ^{− 1} = S^T
• sie ist involutorisch: S² = I
• sie hat die Eigenwerte 1 oder -1.

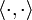Des Weiteren spiegelt S wirklich einen Punkt X (den wir mit seinem Ortsvektor x identifizieren) wie oben beschrieben, da $Sx = x - 2 v v^Tx = x - 2 \langle v, x \rangle v$, wobei $\langle \cdot, \cdot \rangle$ das Skalarprodukt bezeichnet. Beachte, dass $\langle v, x \rangle$ dem Abstand des Punktes X zur Hyperebene 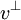$v^\perp$entspricht.

Konstruktion von spezifischen Spiegelungen

Es sei ein Vektor a gegeben, der auf ein Vielfaches des Vektors e gespiegelt werden soll, das heißt, gesucht ist ein Einheitsvektor v mit S_va = λe. Der Einfachheit halber sei e normiert, 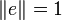$\|e\|=1$. Dann muss, wegen der Orthogonalität der Spiegelung, 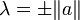$\lambda=\pm\|a\|$ gelten. Der gesuchte Spiegelungsvektor v ergibt sich nun als

$v=\frac{a+\lambda e}{\|a+\lambda e\|}$.

Beide Vorzeichenvarianten führen zum gewünschten Ergebnis (sofern der Nenner von Null verschieden ist). Aus Gründen numerischer Stabilität wird das Vorzeichen von λ so gewählt, dass der Nenner am größten ist.

In der Probe ergibt sich

$\begin{array}{rl} S_va=&a-2v\langle v,a\rangle \\ \\ =&a-2\frac{ (a+\lambda e)\,(\|a\|^2+\lambda\langle e,a\rangle) }{ \|a\|^2+2\lambda\langle a,e\rangle+\lambda^2\|e\|^2} \\ \\ =&a-2(a+\lambda e) \frac{\|a\|^2+\lambda\langle e,a\rangle}{\|a\|^2+2\lambda\langle a,e\rangle+\|a\|^2} \\ \\ =&-\lambda e\\ \\ \end{array}$

Beispiel: Am häufigsten wird der Fall betrachtet, in dem e = e₁ der erste kanonische Basisvektor ist. Sei 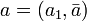$a=(a_1,\bar a)$ in erste Komponente und Restvektor zerlegt. Dann gilt für die Norm 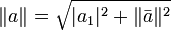$\|a\|=\sqrt{|a_1|^2+\|\bar a\|^2}$. Als Vorzeichen von λ ist das Vorzeichen von a₁ zu wählen, die Richtung der Spiegelung ist dann

$a + \operatorname{sign}(a_1)\,\|a\| e_1 = \Bigl(\operatorname{sign}(a_1)\,(|a_1|+\|a\|),\;\bar a\Bigr)$.

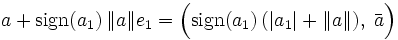Der Vektor v entsteht durch Normierung dieser Richtung. Nach Umformen stellt sich die Norm der Richtung als

$\|a+\lambda e_1\|=\sqrt{2\,\|a\|\,(\|a\|+|a_1|)}$

dar, wobei in dieser Form nur bereits berechnete Zwischenergebnisse benutzt werden. In der unnormierten Variante der Spiegelung ergeben sich weitere Einsparungen an Rechenschritten.

Anwendung: QR-Zerlegung

Householder-Spiegelungen können zur stabilen Berechnung von QR-Zerlegungen einer Matrix 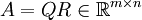$A=QR\in\R^{m\times n}$ verwendet werden, indem zunächst die erste Spalte der Matrix mit einer Spiegelung S₁ auf das Vielfache des ersten Einheitsvektors gespiegelt wird, wie im letzten Abschnitt erläutert (jetzt bezeichnet der Index aber die Nummer der Spiegelung). Danach behandelt man S₁A mit einer Spiegelung S₂ analog und im i-ten Schritt den (i,i) Minoren des Produkts $S_{i-1}\cdots S_1A$ iterativ auf die gleiche Art, bis die Restmatrix Dreieckgestalt R besitzt. 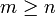Am Ende bekommt man im Fall $m\ge n$ die QR-Zerlegung

$A=QR,\quad Q=S_1S_2\cdots S_{m-1}\in\R^{m\times m},\ R=\begin{pmatrix}R_1\\0\end{pmatrix}\in\R^{m\times n}.$

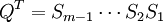Man beachte, dass Q hier eine quadratische Matrix ist und die Dimensionen im Artikel QR-Zerlegung kleiner sind, dort wird nur der wichtige Anteil $A=\tilde Q R_1$, mit den ersten n Spalten $\tilde Q$ von Q betrachtet. Meist wird die Matrix Q nicht explizit berechnet, sondern man nutzt direkt die Produktform, auch bei $Q^T=S_{m-1}\cdots S_2S_1$. Dazu werden die Spiegelvektoren v_i von 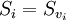$S_i=S_{v_i}$ im frei gewordenen Platz der Matrix A gespeichert.

Die Zahl der Operationen für die QR-Zerlegung einer Matrix 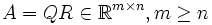$A=QR \in \R^{m\times n},{m \ge n}$ mit dem Householder-Verfahren beträgt:

$\begin{matrix} {m \gg n} &\qquad& {2n^2 \cdot m} \\ {m \approx n} &\qquad& { {4 \over 3} n^3} \end{matrix}$