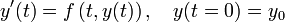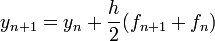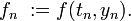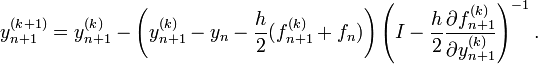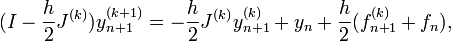Implizites Trapez-Verfahren
- Implizites Trapez-Verfahren
-
Das implizite Trapez-Verfahren ist ein Verfahren zur numerischen Lösung eines Anfangswert-Problems
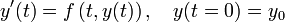
Es lässt sich sowohl den Runge-Kutta-Verfahren als auch den Adams-Moulton-Verfahren zuordnen. Das Trapezverfahren ist A-stabil mit der Besonderheit, dass für die Schwingungslösung y'=iαiy kein Amplitudenfehler auftritt[1]. Das Verfahren lässt sich aus der Trapezregel herleiten:
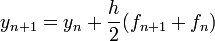
mit
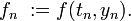
Lösungsmethode
Zur Lösung dieses, in der Regel nichtlinearen Gleichungssystems können verschiedene numerische Verfahren zur Lösung nichtlinearer Gleichungssysteme genutzt werden. Für das quadratisch konvergente Newton-Verfahren ergibt sich konkret:
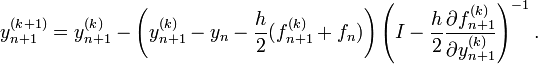
Man erhält also ein lineares Gleichungssystem
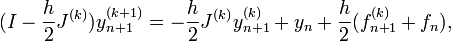
wobei J die Jacobi-Matrix
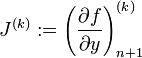 ,
,
I die Einheitsmatrix und k der Iterationsschritt ist.
Schrittweite h
Die (variable) Schrittweite kann aus folgender Beziehung berechnet werden:
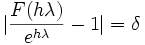 ;
;
δ bezeichnet den zugelassenen lokalen Diskretisierungsfehler. Der Ansatz 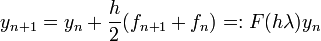 liefert für die implizite Trapez-Methode
liefert für die implizite Trapez-Methode
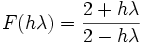 .
.
Dabei ist 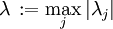 der Betrag des betragsmäßig größten Eigenwerts der Jacobi-Matrix (Spektralradius). Die numerische Bestimmung der Eigenwerte ist sehr zeitaufwendig; für den Zweck der Schrittweitenberechnung ist es im Allgemeinen ausreichend die Gesamtnorm
der Betrag des betragsmäßig größten Eigenwerts der Jacobi-Matrix (Spektralradius). Die numerische Bestimmung der Eigenwerte ist sehr zeitaufwendig; für den Zweck der Schrittweitenberechnung ist es im Allgemeinen ausreichend die Gesamtnorm 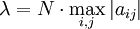 heranzuziehen, die immer größer oder gleich der Spektralnorm ist. N ist der Rang der Jacobi-Matrix und aij deren Elemente.
heranzuziehen, die immer größer oder gleich der Spektralnorm ist. N ist der Rang der Jacobi-Matrix und aij deren Elemente.
Literatur
- H. R. Schwarz: Numerische Mathematik, B.G.Teubner Stuttgart; 1986
Einzelnachweise
- ↑ M. Kloker: Numerische Löser für die Gewöhnliche Modelldifferentialgleichung y'=αy, Universität Stuttgart, 1996
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Runge-Kutta-Verfahren — Einige Runge Kutta Verfahren im Vergleich. Die s stufigen Runge Kutta Verfahren (nach Carl Runge und Martin Wilhelm Kutta) sind Einschrittverfahren zur näherungsweisen Lösung von Anfangswertproblemen in der numerischen Mathematik. Wenn von dem… … Deutsch Wikipedia
Heun-Verfahren — Das Heun Verfahren, benannt nach Karl Heun, ist ein einfaches Verfahren zur numerischen Lösung von Anfangswertaufgaben. Es ist ein Einschrittverfahren und gehört zu der Klasse der Runge Kutta Verfahren. Im Gegensatz zum Expliziten Euler Verfahren … Deutsch Wikipedia
Halbschrittverfahren — Das Heun Verfahren, benannt nach Karl Heun, ist ein einfaches Verfahren zur numerischen Lösung von Anfangswertaufgaben. Es ist ein Einschrittverfahren und gehört zu der Klasse der Runge Kutta Verfahren. Im Gegensatz zum Expliziten Euler Verfahren … Deutsch Wikipedia
Butcher-Tableau — Einige Runge Kutta Verfahren im Vergleich. Die s stufigen Runge Kutta Verfahren (nach Carl Runge und Martin Wilhelm Kutta) sind Einschrittverfahren zur näherungsweisen Lösung von Anfangswertproblemen in der numerischen Mathematik. Wenn vom Runge… … Deutsch Wikipedia
Runge-Kutta — Einige Runge Kutta Verfahren im Vergleich. Die s stufigen Runge Kutta Verfahren (nach Carl Runge und Martin Wilhelm Kutta) sind Einschrittverfahren zur näherungsweisen Lösung von Anfangswertproblemen in der numerischen Mathematik. Wenn vom Runge… … Deutsch Wikipedia
Runge-Kutta-Methode — Einige Runge Kutta Verfahren im Vergleich. Die s stufigen Runge Kutta Verfahren (nach Carl Runge und Martin Wilhelm Kutta) sind Einschrittverfahren zur näherungsweisen Lösung von Anfangswertproblemen in der numerischen Mathematik. Wenn vom Runge… … Deutsch Wikipedia
Ratengleichungen — beschreiben die zeitlichen Konzentrationsverläufe verschiedener Spezies, zum Beispiel bei gekoppelten chemischen Reaktionen, oder bei An und Abregungsprozessen verschiedener Niveaus bei Atomen oder Molekülen: (Gl.1) die an den Reaktionen… … Deutsch Wikipedia
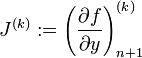 ,
,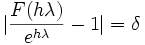 ;
;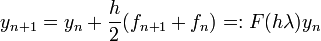 liefert für die implizite Trapez-Methode
liefert für die implizite Trapez-Methode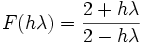 .
.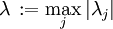 der Betrag des betragsmäßig größten Eigenwerts der Jacobi-Matrix (Spektralradius). Die numerische Bestimmung der Eigenwerte ist sehr zeitaufwendig; für den Zweck der Schrittweitenberechnung ist es im Allgemeinen ausreichend die Gesamtnorm
der Betrag des betragsmäßig größten Eigenwerts der Jacobi-Matrix (Spektralradius). Die numerische Bestimmung der Eigenwerte ist sehr zeitaufwendig; für den Zweck der Schrittweitenberechnung ist es im Allgemeinen ausreichend die Gesamtnorm 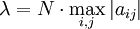 heranzuziehen, die immer größer oder gleich der Spektralnorm ist. N ist der Rang der Jacobi-Matrix und aij deren Elemente.
heranzuziehen, die immer größer oder gleich der Spektralnorm ist. N ist der Rang der Jacobi-Matrix und aij deren Elemente.