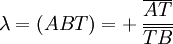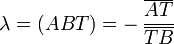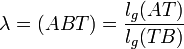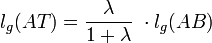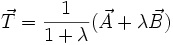Innere Teilung

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

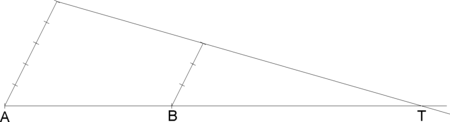
Unter dem Teilverhältnis versteht man in der Geometrie eine Zahl, die die Position eines Punktes in Bezug auf eine gegebene Strecke festlegt. Als Formelzeichen wird häufig λ verwendet. Teilt der Punkt T die Strecke [AB], so schreibt man für das Teilverhältnis λ = TV(ABT) oder, wenn die Bedeutung aus dem Zusammenhang klar ist, häufiger noch einfach λ = (ABT).

Ein Teilverhältnis wird auch für den Fall definiert, dass T nicht auf der Strecke [AB] liegt, sondern auf deren Verlängerung (äußere Teilung).

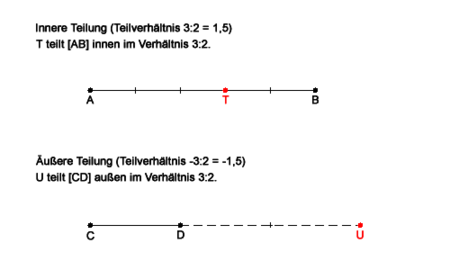
Innere Teilung

Innere und äußere Teilung einer Strecke

Gegeben seien eine Strecke [AB] und ein von B verschiedener Punkt T auf [AB]. Dann ist das Teilverhältnis definiert durch

$\lambda = (ABT) = +\,\frac{\overline{AT}}{\overline{TB}}$

Einfache Teilverhältnisse werden in der Regel als Brüche angegeben; statt λ = 1,5 schreibt man „Teilverhältnis 3:2“ und spricht dies „3 zu 2“.

Wenn T mit B zusammenfällt, kann man λ = ∞ festsetzen.

Äußere Teilung

Liegt T auf der Geraden AB, jedoch nicht auf der Strecke [AB], so ist

$\lambda = (ABT) = -\,\frac{\overline{AT}}{\overline{TB}}$

Bei einer äußeren Teilung ist das Teilverhältnis also stets eine negative Zahl. Statt „λ = −1,5“ sagt man jedoch in der Regel „T teilt [AB] außen im Verhältnis 3:2“

Vertauschung von A und B

Beim Teilverhältnis wird [AB] als „gerichtete Strecke“ aufgefasst; es wird also zwischen Anfangs- und Endpunkt der Strecke unterschieden. Teilt ein Punkt die Strecke [AB] im Teilverhältnis λ, so teilt er [BA] im Teilverhältnis 1/λ. Als Formel:

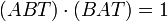$(ABT)\cdot(BAT)=1$ für T ≠ A und T ≠ B

Dies gilt für die innere wie auch für die äußere Teilung.

Zeichnerisches Ermitteln des Teilpunkts

Die Strecke [AB] wird durch T innen im Verhältnis 5:3 geteilt

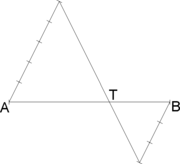
Um den Teilpunkt zu finden, verwendet man eine Konstruktion nach dem zweiten Strahlensatz: Soll die Strecke [AB] im Verhältnis m:n geteilt werden, so zeichnet man durch A und durch B zwei parallele Geraden. Auf der Parallelen durch A trägt man m-mal, auf der Parallelen durch B n-mal die gleiche Strecke ab. Bei innerer Teilung muss das Abtragen in verschiedener Richtung, bei äußerer Teilung in gleicher Richtung erfolgen. Man zeichnet die Gerade durch die Endpunkte der abgetragenen Strecken. Ihr Schnittpunkt mit der Geraden AB ist der gesuchte Teilpunkt.

Die Strecke [AB] wird durch T außen im Verhältnis 5:3 geteilt

Einheitliche Definition des Teilverhältnisses

Die Fallunterscheidung in innere und äußere Teilung lässt sich dadurch verlagern, dass man das Konzept der gerichteten Strecke verwendet und den Längen der gerichteten Strecken ein Vorzeichen zuschreibt: Der Wert von l_g(AT) (gerichtete Streckenlänge) beziehungsweise l_g(BT) soll negativ sein, wenn die entsprechende Strecke entgegengesetzt zu [AB] verläuft.

Mit dieser Festsetzung kann man (für T≠B) einheitlich definieren:

$\lambda = (ABT) = \frac{l_g(AT)}{l_g(TB)}$

Die gerichteten Strecken können auch als Vektoren aufgefasst werden. Da für Vektoren der Quotient nicht definiert ist, setzt man dann fest:

Das Teilverhältnis des Punktes T bezüglich der Strecke [AB] ist die (für 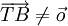$\overrightarrow{TB}\ne\vec o$) eindeutig bestimmte Zahl λ, für die gilt

$\overrightarrow{AT} \, = \, \lambda \, \overrightarrow{TB}$.

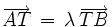Eine einheitliche Darstellung erhält man ebenfalls, wenn AB eine Zahlengerade ist. Haben A, B und T die Zahlenwerte a, b und t (t≠b), so ist

$\lambda = \frac{t-a}{b-t}$,

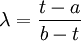und das Vorzeichen ergibt sich automatisch.

Sind die Punkte in einem Parallelkoordinatensystem gegeben durch A(a|a'), und B(b|b') und T(t|t'), so ist

$\lambda = \frac{t-a}{b-t} = \frac{t'-a'}{b'-t'}$.

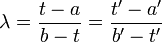Die Teilverhältnisse der Koordinatenabschnitte sind also dieselben wie die auf der Geraden AB. Dies folgt aus dem ersten Strahlensatz.

Goldener Schnitt: (ABS) lässt sich nicht als Verhältnis ganzer Zahlen ausdrücken

Irrationale Teilverhältnisse

Nicht für jeden Teilpunkt T ist es möglich, das Teilverhältnis als ein Verhältnis ganzer Zahlen anzugeben. Dies herausgefunden zu haben ist eine hervorragende Leistung bereits der griechischen Mathematik. So ist zum Beispiel das Teilverhältnis beim goldenen Schnitt (λ = 1/2 + √5 /2) eine irrationale Zahl, die sich nicht in der Form m:n (mit ganzzahligem m und n) schreiben lässt.

Dagegen entspricht jedem Punkt T der Geraden AB (außer dem Punkt B) eine reelle Zahl als Teilverhältnis (ABT). Umgekehrt kann man sagen, dass die Teilverhältnisse (ABT), wenn T die Gerade AB durchwandert, alle reellen Zahlen und den Wert ∞ annehmen.

Teilverhältnis beim Teilen der Einheitsstrecke

Das Teilverhältnis erzeugt also eine umkehrbar eindeutige Abbildung der (bei B gelochten) Gerade AB auf die Menge der reellen Zahlen. Nimmt man als Strecke [AB] das Intervall [0;1] der Zahlengeraden und als Teilpunkt den Punkt x, so entspricht dieser Abbildung der Funktionsterm $\lambda = \frac {x}{1-x}$.

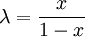Rechnerische Bestimmung des Teilpunkts

Wenn die Strecke [AB] und das Teilverhältnis λ gegeben sind, berechnet man die gerichtete Länge der Strecke [AT] nach der Formel

$l_g(AT) = \frac{\lambda}{1+\lambda}\ \cdot l_g(AB)$

Liegt λ zwischen 0 und −1, so ergibt sich für l_g(AT) ein negativer Wert. T ist dann auf der Seite der Geraden AB einzutragen, auf der (von A aus gesehen) B nicht liegt.

Sind die Punkte A(a|a') und B(b|b') in einem Parallelkoordinatensystem gegeben, so sind die Koordinaten von T

$t=\frac{1}{1+\lambda}(a+\lambda \,b), \ t'=\frac{1}{1+\lambda}(a'+\lambda \,b')$.

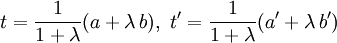Sind A und B durch ihre Ortsvektoren gegeben, ist

$\vec{T} = \frac{1}{1+\lambda} (\vec{A} + \lambda \vec{B})$

Affine Geometrie

Das Teilverhältnis ist eine Invariante jeder affinen Abbildung, d.h. es behält bei Anwendung einer solchen Abbildung (beispielsweise einer Spiegelung oder einer zentrischen Streckung) seinen Wert. Die Eigenschaft kann als kennzeichnendes Merkmal der affinen Geometrie angesehen werden. Siehe dazu: Erlanger Programm.

Siehe auch

• harmonische Teilung
• Doppelverhältnis

Weblinks

• Veranschaulichung der inneren und äußeren Teilung einer Strecke (durch Dynamische Geometrie)