Inverse Winkelfunktion

Inverse Winkelfunktion

Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel.

Die Arkusfunktionen lauten damit Arkussinus, Arkuskosinus, Arkustangens, Arkuscotangens, Arkussekans und Arkuskosekans

Da die trigonometrischen Funktionen periodisch sind, sind sie nicht vollständig invertierbar. Nach der Beschränkung auf ihre Monotonieintervalle kann die eingeschränkte Funktion jedoch invertiert werden.

Die Arkusfunktionen werden durch ein vorangestelltes arc von den trigonometrischen Funktionen unterschieden: 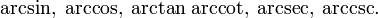\rm arcsin,\; arccos,\; arctan\; arccot,\;arcsec,\; arccsc. Teilweise, vor allem im englischsprachigen Raum, werden sie auch mit 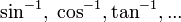\sin^{-1},\; \cos^{-1},\tan^{-1},... bezeichnet.

Für die Umrechnungsfunktion vom Grad- in das Bogenmaß eines Winkels ist der Funktionsname arc oder arcus ohne weitere Zusätze üblich. Arc α (oder arcus α) bezeichnet somit das Bogenmaß des in Grad angegebenen Winkels α.

Weblinks

Trigonometrische Funktion

Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und Kosekans 

Umkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und Arkuskosekans 

Hyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans Hyperbolicus 

Areafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus 

 

Wikimedia Foundation.

Игры ⚽ Нужен реферат?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Winkelfunktion — Mit trigonometrischen Funktionen oder auch Winkelfunktionen bezeichnet man rechnerische Zusammenhänge zwischen Winkel und Seitenverhältnissen (ursprünglich in rechtwinkligen Dreiecken). Tabellen mit Verhältniswerten für bestimmte Winkel… …   Deutsch Wikipedia

  • Arcus-Funktion — Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel. Die… …   Deutsch Wikipedia

  • Arcus-Funktionen — Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel. Die… …   Deutsch Wikipedia

  • Arcusfunktion — Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel. Die… …   Deutsch Wikipedia

  • Arkus-Funktion — Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel. Die… …   Deutsch Wikipedia

  • Cyklometrische Funktion — Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel. Die… …   Deutsch Wikipedia

  • Zyklometrische Funktion — Eine Arkusfunktion (von lat. arcus „Bogen“) oder inverse Winkelfunktion ist die Umkehrfunktion einer trigonometrischen Funktion. Sie berechnet die Bogenlänge eines Sektors des Einheitskreises x2 + y2 = 1. Ihr Funktionswert ist ein Winkel. Die… …   Deutsch Wikipedia

  • Arkusfunktion — Arkusfunktionen (von lat. arcus „Bogen“) sind, wie es ihre alternative Bezeichnung als inverse Winkelfunktionen andeutet, Umkehrfunktionen trigonometrischer Funktionen, die zu einem gegebenen Winkelfunktionswert den zugehörigen Winkel im Bogenmaß …   Deutsch Wikipedia

  • Exponent (Mathematik) — Das Potenzieren ist wie das Multiplizieren seinem Ursprung nach eine abkürzende Schreibweise für eine wiederholte mathematische Rechenoperation. Wie beim Multiplizieren ein Summand wiederholt addiert wird, so wird beim Potenzieren ein Faktor… …   Deutsch Wikipedia

  • Hochrechenen — Das Potenzieren ist wie das Multiplizieren seinem Ursprung nach eine abkürzende Schreibweise für eine wiederholte mathematische Rechenoperation. Wie beim Multiplizieren ein Summand wiederholt addiert wird, so wird beim Potenzieren ein Faktor… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”