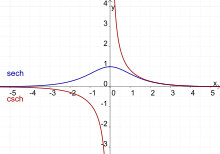
- Sekans Hyperbolicus und Kosekans Hyperbolicus
-
Die Funktionen Kosekans Hyperbolicus (csch) und Sekans Hyperbolicus (sech) sind Hyperbelfunktionen. Sie ergeben sich als Kehrwert von Sinus Hyperbolicus bzw. Kosinus Hyperbolicus.
Inhaltsverzeichnis
Definitionen
Eigenschaften
Sekans Hyperbolicus Kosekans Hyperbolicus Definitionsbereich 

Wertebereich 

Periodizität keine keine Monotonie x < 0 streng monoton steigend
x > 0 streng monoton fallendx > 0 streng monoton fallend
x < 0 streng monoton fallendSymmetrien Spiegelsymmetrie zur y-Achse Punktsymmetrie zum Koordinatenursprung Asymptote  für
für 
 für
für 
Nullstellen keine keine Sprungstellen keine keine Polstellen keine x = 0 Extrema Maximum bei x = 0 keine Wendepunkte 
keine Umkehrfunktionen
Die Umkehrfunktion sind die entsprechenden Areafunktionen:
Ableitungen
Integrale
Reihenentwicklungen
Komplexes Argument
Siehe auch
Weblinks
- Eric W. Weisstein: Hyperbolic Secant und Hyperbolic Cosecant auf MathWorld
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.