Arkussinus und Arkuskosinus

Der Arkussinus - geschrieben arcsin, asin, und Arkuskosinus - geschrieben arccos, acos,sind die Umkehrfunktionen der eingeschränkten Sinus- und Kosinusfunktion: Da Sinus und Kosinus periodische Funktionen sind, muss dabei zu ihrer Umkehrung der ursprüngliche Definitionsbereich des Sinus auf das Intervall [ − π / 2;π / 2] sowie der des Kosinus auf das Intervall [0;π] beschränkt werden.

Zusammen mit dem Arkustangens als Umkehrfunktion des Tangens bilden der Arkussinus und Arkuskosinus den Kern der Klasse der Arkusfunktionen. Aufgrund der heute für Umkehrfunktionen gebräuchlichen allgemeinen Schreibweise f ^{− 1} beginnen dabei aber auch in diesem Fall die namentlich auf Taschenrechnern verbreiteten Schreibweisen sin  ^{− 1} und cos  ^{− 1} die klassische Schreibweise arcsin  bzw. arccos  zu verdrängen, was eventuell zu Verwechslungen mit den Kehrwerten des Kosinus und Sinus (Sekans und Kosekans) führen kann.^[1]

Definitionen

Die Sinusfunktion ist 2π-periodisch und innerhalb einer Periode nicht injektiv. Daher muss ihr Definitionsbereich eingeschränkt werden, damit sie umkehrbar-eindeutig wird. Da es für diese Einschränkung mehrere Möglichkeiten gibt, spricht man von Zweigen des Arkussinus. Meist wird der Hauptzweig (oder Hauptwert), die Umkehrfunktion der Einschränkung $\sin|_{\left[-\frac{\pi}{2},\frac{\pi}{2}\right]}$ betrachtet. In diesem Fall entsteht die bijektive Funktion mit

$\arcsin\colon[-1,1]\to \left[-\frac{\pi}{2},\frac{\pi}{2} \right].$

Analog zum Arkussinus wird der Hauptwert des Arkuskosinus definiert als die Umkehrfunktion von cos  | _[0,π]. Diese Definition führt zu der bijektiven Funktion

$\arccos\colon[-1,1]\to[0,\pi],$

die sich mittels $\arccos x = \frac{\pi}{2} - \arcsin x$ ineinander umrechnen lassen.

Eigenschaften

	Arkussinus	Arkuskosinus
Funktions- Graphen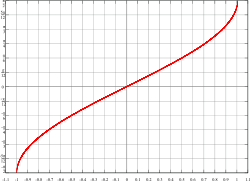
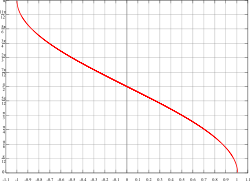
Definitionsbereich	$x\in [-1,1]$	$x\in [-1,1]$
Wertebereich	$-\frac{\pi}{2} \le f(x) \le + \frac{\pi}{2}$	$0\le f(x) \le\pi$
Monotonie	streng monoton steigend	streng monoton fallend
Symmetrien	Ungerade Funktion: $\arcsin(-x) = -\arcsin(x)\!$	Punktsymmetrie zu $\left(x=0\;,\;y =\tfrac{\pi}{2}\right),$ $\arccos(x) = \pi - \arccos(-x)\!$
Asymptoten	$f(x) \to\pm \frac{\pi}{2}$ für $x \to\pm 1$	$f(x) \to \frac{\pi}{2} \mp \frac{\pi}{2}$ für $x \to\pm 1$
Nullstellen	$x = 0\!$	$x = 1\!$
Sprungstellen	keine	keine
Polstellen	keine	keine
Extrema	keine	keine
Wendepunkte	$x = 0\!$	$x = 0\!$

Formeln für negative Argumente

Aufgrund der Symmetrieeigenschaften gilt:

$\arcsin(-x) = -\arcsin(x)\,$

$\arccos(-x) = \pi - \arccos(x)\,$

Reihenentwicklungen

Die Taylorreihe des Arkussinus erhält man durch Anwenden der binomischen Reihe auf die Ableitung, sie ist gegeben durch:

$\arcsin(x) = \sum_{k=0}^{\infty} \frac{(2k-1)!!}{(2k)!!} \frac{x^{2k+1}}{2k+1} = \sum_{k=0}^{\infty} \binom{2k}{k} \frac{x^{2k+1}}{4^{k}(2k+1)} = x \;+\; \frac{1}{2}\cdot\frac{x^3}{3} \;+\; \frac{3}{2\!\cdot\!4}\cdot\frac{x^5}{5} \;+\; \frac{3\!\cdot\!5}{2\!\cdot\!4\!\cdot\!6}\cdot\frac{x^7}{7} \;+\; \ldots$

Der Ausdruck k!! bezeichnet dabei die Doppelfakultät.

Die Taylorreihe des Arkuskosinus ist aufgrund der Beziehung $\arccos x = \frac{\pi}{2} - \arcsin x$ :

$\arccos(x) = \frac{\pi}{2} - \sum_{k=0}^{\infty} \frac{(2k-1)!!}{(2k)!!} \frac{x^{2k+1}}{2k+1} = \frac{\pi}{2} - \sum_{k=0}^\infty \binom{2k}{k} \frac{x^{2k+1}}{4^k(2k+1)}$

Beide Reihen haben den Konvergenzradius 1.

Integraldarstellungen

Die Integraldarstellungen des Arkussinus bzw. Arkuskosinus sind gegeben durch:

$\arcsin(x) = \int \limits_0^x \frac{\mathrm{d}t}{\sqrt{1 - t^2}}$

$\arccos(x) = \int \limits_x^1 \frac{\mathrm{d}t}{\sqrt{1 - t^2}}$

Verkettungen mit Sinus und Kosinus

Für die Arkusfunktionen gelten unter anderem folgende Formeln:

$\sin(\arccos(x))=\sqrt{1-x^2}$, denn für $y=\arccos(x)\!$ gilt $y\in \left[ 0, {\pi} \right]$ und $\sin(y)=\sqrt{1-\cos^2 y}$.

$\cos(\arcsin(x))=\sqrt{1-x^2}$, denn für $y=\arcsin(x)\!$ gilt $y\in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$ und $\cos(y)=\sqrt{1-\sin^2 y}$.

$\sin(\arctan(x))=\frac{x}{\sqrt{1+x^2}}$, denn für $y=\arctan(x)\!$ gilt $y\in \left]-\frac{\pi}{2}, \frac{\pi}{2}\right[$ und $\sin(y)=\frac{\tan y}{\sqrt{1+\tan^2y}}$.

$\cos(\arctan(x))=\frac{1}{\sqrt{1+x^2}}$, denn für $y=\arctan(x)\!$ gilt $y\in \left]-\frac{\pi}{2}, \frac{\pi}{2}\right[$ und $\cos(y)=\frac{1}{\sqrt{1+\tan^2y}}$.

Beziehung zum Arkustangens

Von besonderer Bedeutung in älteren Programmiersprachen ohne implementierte Arkussinus- und Arkuskosinusfunktion sind folgende beiden Beziehungen, die es ermöglichen, den Arkussinus und Arkuskosinus aus dem vielleicht implementierten Arkustangens zu berechnen. Auf Grund obiger Formeln gilt:

$\arcsin(x) = \sgn(x) \cdot \arctan \left(\sqrt{\frac{x^2}{1-x^2}} \right)$

$\arccos(x) = \frac{\pi}{2} - \sgn(x) \cdot \arctan \left(\sqrt{\frac{x^2}{1-x^2}} \right)$ .

Ableitungen

Arkussinus

$\frac{\mathrm d}{\mathrm dx} \arcsin (x) = \frac{1}{\sqrt{1-x^2}}$

Arkuskosinus

$\frac{\mathrm d}{\mathrm dx} \arccos(x) = - \frac{1}{\sqrt{1-x^2}}$

Umrechnung

$\frac{\mathrm d}{\mathrm dx} \arccos(x) = - \frac{\mathrm d}{\mathrm dx} \arcsin (x)$

Integrale

Arkussinus

$\int \arcsin\left(\frac{x}{a}\right) \mathrm dx = x\,\arcsin\left(\frac{x}{a}\right) + \sqrt{a^2 - x^2 } + C$

Arkuskosinus

$\int \arccos \left( \frac{x}{a} \right)\, \mathrm dx = x \, \arccos \left( \frac{x}{a} \right) - \sqrt{ a^2 - x^2} + C$

Komplexe Argumente

$\begin{align} \arcsin(a+b\,\mathrm{i}) = \quad \frac{\sgn{a}}{2} \cdot \arccos & \!\left( \sqrt{(a^2+b^2-1)^2 + 4b^2} - (a^2+b^2) \right) \\ +\;\mathrm{i} \cdot \frac{\sgn{b}}{2} \cdot \operatorname{arcosh} & \!\left( \sqrt{(a^2+b^2-1)^2 + 4b^2} + (a^2+b^2) \right) \end{align}$   mit $a,b \in \mathbb{R}$

$\arccos(a+b\,\mathrm{i}) = \frac\pi2 - \arcsin(a+b\,\mathrm{i})$

Wobei für die Signumfunktion gilt $\sgn{x} := \begin{cases} +1 & \; x\geq0 \\ -1 & \; x<0 \\ \end{cases}$, zur Funktion arcosh siehe Areakosinus Hyperbolicus!

Anmerkungen

Besondere Werte

x	− 1	$-\frac{\sqrt{3}}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{1}{2}$	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
arcsin(x)	$-\frac{\pi}{2}$	$-\frac{\pi}{3}$	$-\frac{\pi}{4}$	$-\frac{\pi}{6}$	0	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$

x	− 1	$-\frac{\sqrt{3}}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{1}{2}$	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
arccos(x)	π	$\frac{5 \pi}{6}$	$\frac{3 \pi}{4}$	$\frac{2 \pi}{3}$	$\frac{\pi}{2}$	$\frac{\pi}{3}$	$\frac{\pi}{4}$	$\frac{\pi}{6}$	0

Kettenbruchdarstellung des Arkussinus

H. S. Wall fand 1948 für den Arkussinus folgende Kettenbruchdarstellung:

$\arcsin(x)=\frac{x\sqrt{1-x^2}}{1-\cfrac{1\cdot 2x^2}{3-\cfrac{1\cdot 2x^2}{5-\cfrac{3\cdot 4x^2}{7-\cfrac{3\cdot 4x^2}{9-\cfrac{5\cdot 6x^2}{11-\ldots}}}}}}$

Sonstiges

Man kann Arkussinus und Arkuskosinus auch durch den Hauptzweig des komplexen Logarithmus ausdrücken:

$\arcsin z = -\mathrm{i}\,\ln\left(\mathrm i z+\sqrt{1-z^2}\right)$

$\arccos z = -\mathrm{i}\,\ln\left(z+\mathrm i\sqrt{1-z^2}\right)$

Siehe auch

• Formelsammlung Trigonometrie
• Trigonometrische Funktionen

Literatur

• Ilja Bronstein, Konstantin Semendjajew: Taschenbuch der Mathematik. B.G. Teubner, Stuttgart 1991. ISBN 3-87144-492-8

Einzelnachweise

1. ↑ Weisstein, Eric W. "Inverse Trigonometric Functions." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseTrigonometricFunctions.html

Trigonometrische Funktion

Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und Kosekans 

Umkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und Arkuskosekans 

Hyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans Hyperbolicus 

Areafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus