Inzidenz (Mathematik)

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Inzidenz ist in der Geometrie die einfachste Beziehung, die zwischen geometrischen Elementen wie Punkt, Gerade, Kreis, Ebene etc. auftreten kann. Inzidenz soll bestehen, wenn beispielsweise ein Punkt auf einer Geraden liegt oder eine Ebene eine Gerade enthält. Mathematisch gesprochen handelt es sich also um eine Relation, d. h. um eine Teilmenge des kartesischen Produkts der Mengen der Punkte, Geraden etc.

Eine Inzidenzstruktur ist demnach eine Struktur

$\mathfrak{I}=\langle M_1, M_2, \dots,\textbf{F} \rangle$

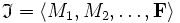
bestehend aus Mengen M_i von Punkten, Geraden, Ebenen etc. zusammen mit einer Relation

$\textbf{F} \subseteq M_1 \times M_2 \times \dots$

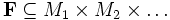
welche die Inzidenz definiert. 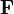$\textbf{F}$ wird auch als Fahnenmenge bezeichnet. Die Automorphismen einer Inzidenzstruktur heißen Kollineationen.

Der Inzidenzbegriff spielt seit David Hilberts axiomatischer Grundlegung eine zentrale Rolle in der Geometrie, da mit Hilberts Ansatz nicht mehr versucht wird, Beschreibungen der „Natur“ von geometrischen Objekten zu geben, sondern diese Objekte allein durch ihre mathematisch fassbaren Beziehungen untereinander definiert werden.

Unter Inzidenzgeometrie versteht man in der Mathematik eine Geometrie, die allein auf den Inzidenzaxiomen (und eventuell einem weiteren Existenzaxiom) beruht.

Sprechweisen

Neben den bekannten Sprechweisen „ein Punkt p liegt auf einer Geraden G“ oder „eine Ebene 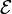$\mathcal{E}$ enthält eine Gerade G“ für „p inzidiert mit G“ bzw. „G inzidiert mit 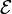$\mathcal{E}$“ sind auch folgende Ausdrücke üblich:

• Inzidieren zwei (verschiedene) Geraden mit demselben Punkt, ist dies der Schnittpunkt der Geraden.
• Inzidieren zwei (verschiedene) Punkte mit derselben Geraden, ist diese die Verbindungsgerade der Punkte.
• Inzidieren mehrere Punkte mit derselben Geraden, heißen sie kollinear.
• Inzidieren mehrere Geraden mit demselben Punkt, heißen sie kopunktal.

Beispiele für Inzidenzstrukturen

• affine und projektive Ebenen
• Polygone und Polyeder
• Euklidischer Raum
• Möbius-Ebene
• Bei geeigneter Definition der Inzidenz aber auch Tische, Stühle und Bierseidel.

Literatur

• Hilbert, David: Grundlagen der Geometrie, Stuttgart - Leipzig: Teubner (14. Auflage 1999)
• F.Buekenhout: Handbook of Incidence Geometry. North Holland 1995. ISBN 978-0-444-88355-1

Weblinks

• Inzidenzgeometrie bei PlanetMath