- Möbius-Ebene
-
Eine Möbius-Ebene, benannt nach August Ferdinand Möbius, ist eine Struktur in der Inzidenzgeometrie. Die ursprüngliche Motivation für die (axiomatische) Definition von Möbius-Ebenen ist die Struktur, die man erhält, wenn man die Inzidenzrelation von Punkten und Kreisen auf einer Kugeloberfläche untersucht.
Inhaltsverzeichnis
Definition
Eine Inzidenzstruktur M = (P,K,I), für die die nachfolgenden Axiome gelten, wird als Möbius-Ebene bezeichnet. Die Elemente von P werden in diesem Zusammenhang üblicherweise als Punkte und die Elemente von K als Kreise bezeichnet.
- (M1) Je 3 paarweise verschiedene Punkte inzidieren mit genau einem Kreis.
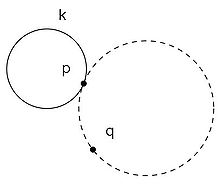
- (M2) Sind p und q zwei Punkte von M und k ein Kreis durch p, der q nicht enthält, dann gibt es genau einen Kreis, der mit p und q inzidiert und den Kreis k berührt. Dies wird auch als Berühraxiom bezeichnet
- (M3) Es gibt 4 Punkte, die nicht mit einem gemeinsamen Kreis inzidieren und jeder Kreis inzidiert mit mindestens einem Punkt.
Ein Beispiel
Die kleinste Möbius-Ebene erhält man, wenn man eine Menge aus 5 Punkten mit allen 3-elementigen Teilmengen betrachten und als Inzidenzrelation das Enthaltensein wählt. Also hat man eine Inzidenzstruktur M = (P,K,I) mit
 ,
,  und
und  für alle
für alle  .
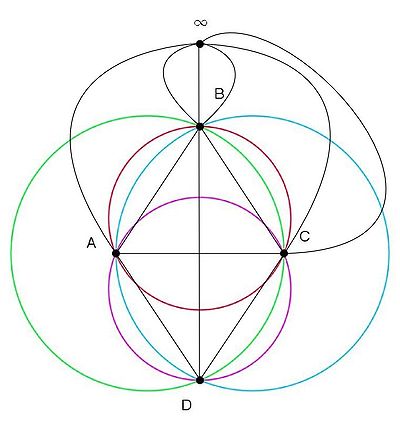
.Die kleinste Möbius-Ebene mit 5 Punkten Zusammenhang mit affinen Ebenen
Sei M = (P,K,I) eine Inzidenzstruktur, in der jeder Kreis mit mindestens einem Punkt inzidiert und bezeichnet Mp die Ableitung der Inzidenzstruktur M in einem Punkt p, dann gilt der folgende Satz:
M ist genau dann eine Möbius-Ebene, wenn Mp für alle Punkte p eine affine Ebene ist.
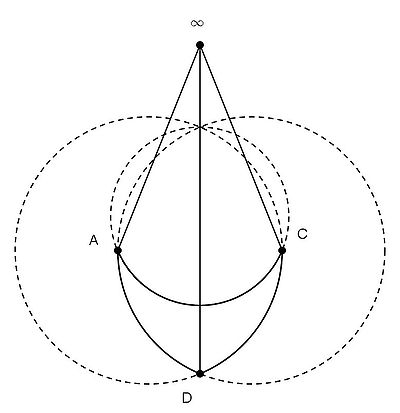
Ableitung der kleinsten Möbius-Ebene nach einem Punkt: 
Die klassische Möbius-Ebene
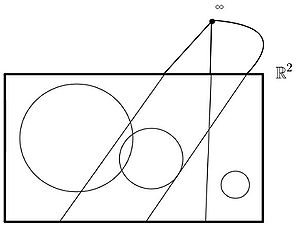
Die klassische Möbius-Ebene erhält man als Inzidenzstruktur aus der reellen affinen Ebene
 , indem man Geraden und Kreise von
, indem man Geraden und Kreise von  als Blöcke wählt. Damit das Verhalten von Geraden und Kreisen möglichst gleichartig ist, so dass sich zum Beispiel Geraden wie Kreise in genau 2 Punkten schneiden oder in einem Punkt berühren, erweitert man
als Blöcke wählt. Damit das Verhalten von Geraden und Kreisen möglichst gleichartig ist, so dass sich zum Beispiel Geraden wie Kreise in genau 2 Punkten schneiden oder in einem Punkt berühren, erweitert man  um einen Punkt
um einen Punkt  in dem sich alle Geraden schneiden. Somit erhält man die Inzidenzstruktur M = (P,K,I) mit
in dem sich alle Geraden schneiden. Somit erhält man die Inzidenzstruktur M = (P,K,I) mit  ,
,  und
und  für alle
für alle  .
.Da die stereographische Projektion eine Kugeloberfläche bis auf den Nordpol in die reelle affine Ebene abbildet und dabei Kreise auf der Kugeloberfläche in Kreise oder Geraden in der Ebene abbildet, ist die obige Konstruktion isomorph zur Inzidenzstruktur, die die Punkte und Kreise auf einer Kugeloberfläche bilden. Dabei entspricht der Nordpol dem Punkt
 und die Kreise auf der Kugeloberfläche, die durch den Nordpol gehen, den Geraden in der Ebene.
und die Kreise auf der Kugeloberfläche, die durch den Nordpol gehen, den Geraden in der Ebene.Literatur
- A. Beutelspacher: Einführung in die endliche Geometrie II. S. 116, Bibliographisches Institut, 1983, ISBN 3-411-01648-5
- J.H. van Lint, R.M. Wilson: A Course in Combinatorics. S. 323, Cambridge University Press, 1992, ISBN 0-521-42260-4
Weblinks
Wikimedia Foundation.