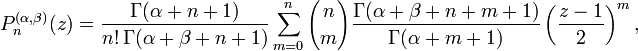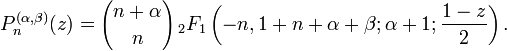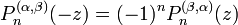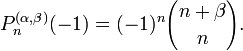Jacobi — ist der Familienname folgender Personen: Abraham Jacobi (1830–1919), deutsch US amerikanischer Kinderarzt Albano von Jacobi (1854–1928), deutscher Offizier und Diplomat Ariane Jacobi (* 1966), deutsche Jazzsängerin und Moderatorin Arnold Jacobi… … Deutsch Wikipedia
Jacobi-Polynom — Die Jacobi Polynome (nach Carl Gustav Jacob Jacobi), auch hypergeometrische Polynome sind eine Menge polynomieller Lösungen des Sturm Liouville Problems, die einen Satz orthogonaler Polynome bilden, und zwar auf dem Intervall [ 1,1] bezüglich der … Deutsch Wikipedia
Polynome de Jacobi — Polynôme de Jacobi En mathématiques, les polynômes de Jacobi sont une classe de polynômes orthogonaux. Ils sont obtenus à partir des séries hypergéométriques dans les cas où la série est en fait finie : où est le symbole de Pochhammer pour… … Wikipédia en Français
Polynôme de jacobi — En mathématiques, les polynômes de Jacobi sont une classe de polynômes orthogonaux. Ils sont obtenus à partir des séries hypergéométriques dans les cas où la série est en fait finie : où est le symbole de Pochhammer pour la factorielle… … Wikipédia en Français
JACOBI (C.) — Le mathématicien allemand Carl Jacobi fut, avec N. H. Abel, le fondateur de la théorie des fonctions elliptiques dont il donna de nombreuses applications aux branches les plus diverses des mathématiques. On lui doit également des exposés de… … Encyclopédie Universelle
Polynôme de Jacobi — En mathématiques, les polynômes de Jacobi sont une classe de polynômes orthogonaux. Ils sont obtenus à partir des séries hypergéométriques dans les cas où la série est en fait finie : où est le symbole de Pochhammer pour la factorielle… … Wikipédia en Français
Jacobi-Operator — Ein Jacobi Operator, nach Carl Gustav Jakob Jacobi, ist ein symmetrischer linearer Operator der auf Folgen operiert und der in der durch Kronecker Deltas gegebenen Standardbasis durch eine tridiagonale Matrix dargestellt wird. Selbstadjungierte… … Deutsch Wikipedia
Polynôme de Legendre — Polynômes de Legendre Les polynômes de Legendre sont des solutions de l équation différentielle de Legendre, et constituent l exemple le plus simple d une suite de polynômes orthogonaux. Sommaire … Wikipédia en Français
polynôme hypergéométrique — hipergeometrinis daugianaris statusas T sritis fizika atitikmenys: angl. hypergeometric polynomial; Jacobi polynomial vok. hypergeometrisches Polynom, n rus. гипергеометрический полином, m; полином Якоби, m pranc. polynôme hypergéométrique, m … Fizikos terminų žodynas
Jacobi polynomial — hipergeometrinis daugianaris statusas T sritis fizika atitikmenys: angl. hypergeometric polynomial; Jacobi polynomial vok. hypergeometrisches Polynom, n rus. гипергеометрический полином, m; полином Якоби, m pranc. polynôme hypergéométrique, m … Fizikos terminų žodynas
 .
.