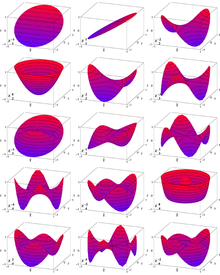
- Zernike-Polynom
-
Die Zernike-Polynome sind nach Frits Zernike benannte orthogonale Polynome, und spielen insbesondere in der geometrischen Optik eine wichtige Rolle. Es gibt gerade und ungerade Zernike-Polynome. Die geraden Zernike-Polynome sind definiert durch:
und die ungeraden durch
wobei m und n nichtnegative ganze Zahlen sind für die gilt:
 . ϕ ist der azimutale Winkel und ρ ist der normierte radiale Abstand.
. ϕ ist der azimutale Winkel und ρ ist der normierte radiale Abstand.Die Radialpolynome
 sind als
sind alsund
 , wenn n − m ungerade ist, definiert.
, wenn n − m ungerade ist, definiert.Inhaltsverzeichnis
Eigenschaften
Zernike-Polynome können durch ein Produkt eines radiusabhängigen Teil
 und eines winkelabhängigen Teils Gm dargestellt werden:
und eines winkelabhängigen Teils Gm dargestellt werden:Der winkelabhängige Teil hat die Eigenschaft, dass eine Rotation des Koordinatensystems um den Winkel α = 2π / m die Form des Polynoms nicht ändert:
Der radiusabhängige Teil ist ein Polynom über ρ vom Grad n, welches keine Potenz kleiner m enthält.
 ist eine gerade (ungerade) Funktion, wenn m gerade (ungerade) ist.
ist eine gerade (ungerade) Funktion, wenn m gerade (ungerade) ist.Der radiusabhängige Teil stellt einen Spezialfall der Jacobi-Polynome
 dar.
dar.Die Reihe der radiusabhängigen Polynome beginnt mit
Allgemein ist

Anwendungen
In der Optik werden Zernike-Polynome benutzt um Wellenfronten zu repräsentieren, die wiederum die Abbildungsfehler von optischen Systemen beschreiben. Dies findet zum Beispiel in der adaptiven Optik Anwendung.
Seit einigen Jahren ist die Verwendung von Zernike-Polynomen auch in der Optometrie und Augenheilkunde üblich. Hier führen Abweichungen der Cornea beziehungsweise der Linse von der idealen Form zu Abbildungsfehlern.
Literatur
- Born and Wolf: Principles of Optics. Oxford: Pergamon, 1970.
Weblinks
- Eric W. Weisstein: Zernike Polynomial. In: MathWorld. (englisch)
Wikimedia Foundation.