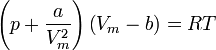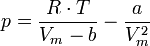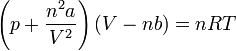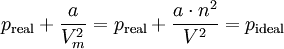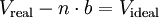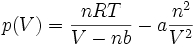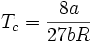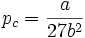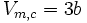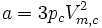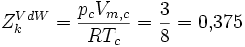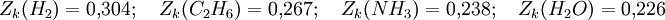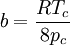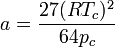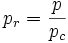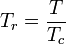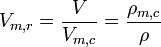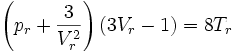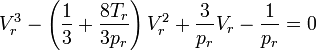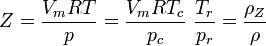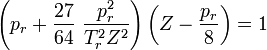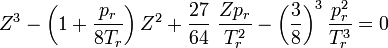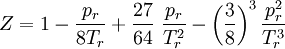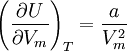Kohäsionsdruck

Die Van-der-Waals-Gleichung ist eine angenäherte Zustandsgleichung für reale Gase. Sie wurde 1873 durch Johannes Diderik van der Waals aufgestellt, wofür er 1910 den Nobelpreis für Physik erhielt.

Gas	a in (kPa·dm6)/mol2	b in dm3/mol
Helium (He)	3,45	0,0237
Neon (Ne)	21,3	0,0171
Argon (Ar)	136,3	0,0322
Wasserstoff (H2)	24,7	0,0266
Stickstoff (N2)	140,8	0,0391
Sauerstoff (O2)	137,8	0,0318
Luft (80% N2, 20% O2)	135,8	0,0364
Kohlendioxid (CO2)	363,7	0,0427
Wasser (H2O)	557,29	0,031
Chlor (Cl2)	657,4	0,0562
Ammoniak (NH3)	422,4	0,0371
Methan (CH4)	225	0,0428
Die hier integrierten Messergebnisse verschiedener Gruppen unterliegen teilweise recht großen Schwankungen.
Benzol (C6H6)	52,74	0,3043
Decan (C10H22)	37,88	0,2374
Octan (C8H18)	18,82	0,1193
Die hier integrierten Literaturwerte basieren auf „technisch reinen“ Stoffen. Sie gelten selbstverständlich nicht für Flüssigkeiten, sondern in der Gasphase.

Beschreibung

Sie lautet in der intensiven Form:

$\left( p + \frac{a}{V^2_m}\right)\left(V_m - b \right) = RT$

$p = \frac{R \cdot T}{V_m - b}-\frac{a}{V^2_m}$

und in der extensiven Form:

$\left( p + \frac{n^2 a}{V^2}\right)\left(V-nb \right) = nRT$

Die einzelnen Formelzeichen stehen für folgende Größen:

• V - Volumen
• V_m - molares Volumen
• n - Stoffmenge
• T - Temperatur
• p - Druck
• R - universelle Gaskonstante
• a - Kohäsionsdruck (Tabellen rechts)
• b - Kovolumen (Tabellen rechts)

Eine andere und vom Prinzip her „beliebig“ genaue Näherungslösung ist die Reihenentwicklung der Virialgleichungen, wobei die Zustandsgleichung idealer Gase, auf welcher auch die Van-der-Waals-Gleichung aufbaut, identisch mit einem Abbruch dieser Reihenentwicklung nach dem ersten Glied ist.

Ursachen und Herleitung

Gase verhalten sich in der Praxis nicht exakt nach dem einfachen Modell des idealen Gases, da sie aus Molekülen mit einer Ausdehnung größer als null bestehen. Das Modell des idealen Gases ignoriert, dass reale Gasteilchen ein Eigenvolumen besitzen, was dazu führt, dass das Volumen realer Gase größer ist als das Volumen eines idealen Gases (V_ideal < V_real). Zudem gibt es zwischen den Teilchen realer Gase Wechselwirkungen, die über elastische Stöße idealer Gase hinaus gehen. Die zwischenmolekularen Anziehungskräfte realer Gase bedingen hierbei, besonders bei einem hohen Druck, dass der Gasdruck des realen Gases unter dem Druck des idealen Gases liegt (p_real < p_ideal).

Ideale Gase könnten beispielsweise (theoretisch) niemals in einen flüssigen oder festen Aggregatzustand übergehen, unabhängig davon, wie sehr sie gekühlt oder komprimiert werden. Daher sind für reale Gase Modifikationen der Gasgesetze idealer Gase notwendig. Die Van-der-Waals-Gleichung ergibt sich, im Gegensatz zur allgemeinen Gasgleichung, für ein Modellgas aus starren Kugeln mit anziehender Dipol-Wechselwirkung, was folgende Anpassungen notwendig macht:

$p_{\rm real} + \frac{a}{V_m^2} = p_{\rm real} + \frac{a \cdot n^2}{V^2} = p_{\rm ideal} \!$

$V_{\rm real} - n \cdot b = V_{\rm ideal} \!$

Setzt man dies in die allgemeine Gasgleichung ein, so erhält man die Van-der-Waals-Gleichung.

Die Parameter a und b sind experimentell bestimmte Daten, die oft selbst keine Konstanten darstellen und ihrerseits von anderen Größen abhängen. Das Kovolumen b entspricht in etwa dem Eigenvolumen der Atome von einem Mol des Gases. Der Term a n²/V² berücksichtigt die gegenseitige Anziehung der Gasatome (Van-der-Waals-Bindung), welche man auch als Binnendruck bezeichnet. Die Van-der-Waals-Gleichung versagt bei hohen Drücken, da das angenommene starre Eigenvolumen der Moleküle eine Kompression auf ein Molvolumen kleiner b nicht zulässt, was dem Verhalten realer Gase widerspricht.

Die Van-der-Waals-Gleichung beschreibt sowohl die Gasphase als auch die Flüssigphase qualitativ richtig, ist jedoch für viele Anwendungen zu ungenau. Hier muss man dann zu genauer beschreibenden Gleichungen greifen, z. B. der Redlich-Kwong-Gleichung oder der Redlich-Kwong-Soave-Gleichung, welche weiterentwickelte, aber auch halbempirische Van-der-Waals-Gleichungen darstellen.

Es gibt auch empirische Zustandsgleichungen, wie z. B. die Benedict-Webb-Rubin-Gleichung.

Isothermen des p-V-Diagramms

Die nach p aufgelöste Van-der-Waals-Gleichung

$p(V) = \frac{n R T}{V - n b} - a\frac{n^2}{V^2}$

stellt im p-V-Diagramm die Differenz einer verschobenen Hyperbel und einer zu 1 / V² proportionalen Funktion dar. Sie entspricht für hohe Temperaturen sowie für niedrige Teilchenzahldichten N/V der Gleichung für ideale Gase. Unterhalb einer kritischen Temperatur T_c jedoch treten beim Durchlaufen einer Isothermen ein Minimum und ein Maximum auf. Man bezeichnet den daraus resultierenden Verlauf der Isotherme als Van-der-Waals-Schleifen.^[1] Diese ergeben jedoch physikalisch keinen Sinn, denn anstatt dem Verlauf der Isotherme zu folgen bleibt der Druck für einen bestimmten Bereich konstant, während sich das Volumen erhöht: Teile des Stoffes verdampfen.

Man kann aus der Isothermen nach der Van-der-Waals-Gleichung die in Experimenten tatsächlich gemessene Isotherme konstruieren. Die Waagerechte im realen pV-Diagramm schneidet die Van-der-Waals-Kurve in drei Punkten. Die beiden hierbei gebildeten Flächen sind gleich groß. Man bezeichnet dies als Maxwell-Konstruktion.

Der Bereich, in dem die Van-der-Waals-Kurve von der tatsächlichen Isothermen abweicht, stellt einen zweiphasigen Bereich des p-V-Diagramms dar, in dem eine flüssige und eine gasförmige Phase koexistieren.

Abschätzung der kritischen Größen

Wie im letzten Abschnitt schon deutlich wurde, spielt der kritische Punkt für reale Gase eine entscheidende Rolle. Es zeigt sich hierbei, dass aus der Van-der-Waals-Gleichung folgende Zusammenhänge ableitbar sind:

Kritische Temperatur:

$T_c = \frac{8a}{27bR}$

Kritischer Druck:

$p_c = \frac{a}{27b^2}$

Kritisches Molvolumen:

$V_{m, c} = 3b \!$

Kombination kritisches Molvolumen und kritischer Druck:

$a = 3 p_c V_{m, c}^2$

Es zeigt sich weiterhin, dass sich eine Konstante ergibt, wenn man die so erhaltenen kritischen Größen in die allgemeine Gasgleichung einsetzt:

$Z_k^{VdW} = \frac{p_c V_{m, c}}{R T_c} = \frac{3}{8} = 0{,}375$

Man bezeichnet diesen Wert als kritischen Kompressibilitätsfaktor. In der Van-der-Waals-Gleichung ist diese wie gezeigt stoffunabhängig konstant, was jedoch nicht realen Gegebenheiten entspricht. In der Regel bewegt er sich in einem Bereich zwischen 0,25 bis 0,3. Diese Abweichung verdeutlicht den Näherungscharakter der Van-der-Waals-Gleichung.

Beispiele:

$Z_k(H_2) = 0{,}304; \quad Z_k(C_2H_6) = 0{,}267; \quad Z_k(NH_3) = 0{,}238; \quad Z_k(H_2O) = 0{,}226$

Siehe auch: Kritischer Exponent

Unter Beachtung dieses Näherungscharakters kann man umgekehrt a und b aus den kritischen Größen berechnen:

$b = \frac{R T_c}{8 p_c}$

$a = \frac{27 (R T_c)^2}{64 p_c}$

Reduzierte Form

Die reduzierten Größen nutzen den für jeden Stoff spezifischen kritischen Punkt als Vergleichsbasis, indem sie die jeweiligen Zustandsgrößen durch ihre kritischen Entsprechungen dividieren. Sie sind daher dimensionslos und werden wie folgt definiert.

Reduzierter Druck:

$p_r = \frac{p}{p_c}$

Reduzierte Temperatur:

$T_r = \frac{T}{T_c}$

Reduziertes Molvolumen (bzw. indirekt reduzierte Dichte, weil die Masse konstant ist):

$V_{m, r} = \frac{V}{V_{m, c}} = \frac{\rho_{m, c}}{\rho}$

Haben zwei Stoffe die gleichen reduzierten Größen, so weisen sie auch vergleichbare Eigenschaften auf. Man kann mit ihnen auch die Van-der-Waals-Gleichung in einer reduzierten Form formulieren:

$\left( p_r + \frac{3}{V_r^2} \right) (3 V_r - 1) = 8 T_r$

Das stellt eine Gleichung 3. Grades für das reduzierte Volumen dar:

$V_r^3 - \left(\frac{1}{3} + \frac{8 T_r}{3 p_r}\right) V_r^2 + \frac{3}{p_r} V_r - \frac{1}{p_r} = 0$

Der Kompressionsfaktor Z stellt einen Bezug zum idealen Gasvolumen (bzw. indirekt zur idealen Gasdichte) her:

$Z = \frac{V_m R T}{p} = \frac{V_m R T_c}{p_c}~\frac{T_r}{p_r} = \frac{\rho_Z}{\rho}$

Damit lautet die Van-der-Waals-Gleichung:

$\left( p_r + \frac{27}{64}~\frac{p_r^2}{T_r^2 Z^2}\right) \left (Z - \frac{p_r}{8}\right) = 1$

Das stellt eine Gleichung 3. Grades für den Kompressionsfaktor (bezüglich des idealen Volumens) dar:

$Z^3 - \left(1 + \frac{p_r}{8 T_r}\right) Z^2 + \frac{27}{64}~\frac{Z p_r}{T_r^2} - \left(\frac{3}{8}\right)^3 \frac{ p_r^2}{ T_r^3} = 0$

Eine Näherung für kleine Drücke und/oder hohe Temperaturen ist:

$Z = 1 - \frac{p_r}{8 T_r} + \frac{27}{64}~\frac{p_r}{T_r^2} - \left(\frac{3}{8}\right)^3 \frac{ p_r^2}{ T_r^3}$

Innere Energie

Die Innere Energie eines Van-der-Waals-Gases hängt vom Volumen ab:

$\left( {\partial U \over \partial V_m} \right)_{T} = \frac{a}{V_m^2}$

Sie besteht nicht nur aus der kinetischen Energie der Moleküle, sondern auch aus der potentiellen Energie der Kohäsionskräfte, gegeben durch den Parameter a.

Literatur

• Johannes Diderik van der Waals: Over de Continuiteit van den gas- en vloeistoftoestand. Sijthoff, Leiden 1873, deutsch: Die Kontinuität des gasförmigen und flüssigen Zustandes. Barth, Leipzig 1881
• James Clerk Maxwell: On The dynamical evidence of the moleculkar constitution of bodies. In: Nature. Band 11, 1875, S. 357–359 und 374–377

Einzelnachweise

1. ↑ Isothermen des p-V-Diagramms zur Van-der-Waals-Gleichung