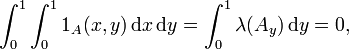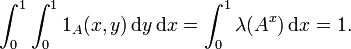- Kontinuumhypothese
-
Die Kontinuumshypothese wurde 1878 vom Mathematiker Georg Cantor aufgestellt. Der Name rührt daher, dass die reellen Zahlen auch als „das Kontinuum“ bezeichnet werden.
Inhaltsverzeichnis
Aussage
Die Hypothese besagt:
- Es gibt keine überabzählbare Teilmenge der reellen Zahlen, die in ihrer Mächtigkeit kleiner ist als die der reellen Zahlen.
Anders ausgedrückt:
- Es gibt keine Menge, deren Mächtigkeit zwischen der Mächtigkeit der natürlichen Zahlen und der Mächtigkeit der reellen Zahlen liegt.
Bezeichnet man, wie üblich, die Kardinalzahl (Mächtigkeit) der natürlichen Zahlen mit
 , die darauf folgende Kardinalzahl mit
, die darauf folgende Kardinalzahl mit 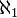 und die Kardinalzahl der reellen Zahlen mit
und die Kardinalzahl der reellen Zahlen mit  , so heißt die Kontinuumshypothese formal:
, so heißt die Kontinuumshypothese formal: 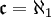
Bedeutung
In der berühmten Liste von 23 mathematischen Problemen, die David Hilbert am Internationalen Mathematikerkongress 1900 in Paris vortrug, steht die Kontinuumshypothese an erster Stelle.
Lösung
Das Problem ist heute gelöst, wenn auch nicht in dem Sinne, wie Hilbert dies erwartet hatte:
Kurt Gödel bewies 1938,[1] dass die Kontinuumshypothese (CH) zur Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom (ZFC) relativ widerspruchsfrei ist, d. h.: Wenn ZFC widerspruchsfrei ist (was allgemein angenommen wird, aber nach dem Gödelschen Unvollständigkeitssatz nicht mit Hilfe von ZFC bewiesen werden kann), dann ist auch "ZFC + CH" widerspruchsfrei. Das bedeutet:
- Aus der Zermelo-Fraenkel-Mengenlehre lässt sich die Kontinuumshypothese nicht widerlegen!
In den 1960er Jahren zeigte Paul Cohen:
- Aus der Zermelo-Fraenkel-Mengenlehre lässt sich die Kontinuumshypothese auch nicht beweisen!
Anders ausgedrückt: Auch die Negation der Kontinuumshypothese ist zu ZFC relativ widerspruchsfrei; die Kontinuumshypothese ist also insgesamt unabhängig von ZFC.
Für diesen Beweis erhielt Cohen die Fields-Medaille.
Daher kann der Kontinuumshypothese im Rahmen der Mengenlehre kein Wahrheitswert zugewiesen werden. Sie kann, ebenso gut wie ihre Negation, als neues Axiom verwendet werden. Damit ist sie das erste relevante Beispiel für Gödels Unvollständigkeitssatz.
Aussagen in „ZFC + CH“
Alternativ werden gelegentlich Aussagen unter der Annahme gemacht, dass die Kontinuumshypothese wahr sei. Es ist jedoch üblich, diese Voraussetzung dann explizit zu erwähnen (während die Tatsache, dass die meisten mathematischen Beweise vor dem Hintergrund eines ZFC-ähnlichen Axiomensystem gemacht werden, im Allgemeinen nicht erwähnt wird).
Verallgemeinerung
Die verallgemeinerte Kontinuumshypothese (GCH) besagt, dass für jede unendliche Menge X zwischen den Kardinalzahlen |X| und 2|X| (der Mächtigkeit der Potenzmenge von X) keine weiteren Kardinalzahlen liegen. Die einfache Kontinuumshypothese (CH) macht diese Behauptung für den Fall X = N. Die verallgemeinerte Kontinuumshypothese ist ebenfalls unabhängig von der Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom (ZFC).
Anwendungsbeispiel
Im Folgenden sei die Kontinuumshypothese als wahr angenommen und ω1 die kleinste überabzählbare Ordinalzahl. Dann gibt es eine Bijektion
![T:[0,1]\rightarrow \omega_1](/pictures/dewiki/54/650623dcb1163c53e758b94b78ffd8d5.png) . Die ordinale Ordnung < auf ω1 werde mithilfe dieser Bijektion auf [0,1] übertragen: Für
. Die ordinale Ordnung < auf ω1 werde mithilfe dieser Bijektion auf [0,1] übertragen: Für ![x,y\in[0,1]](/pictures/dewiki/57/91c753bdf38924b04944eb6b2e5d3353.png) gelte:
gelte: 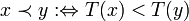 .
.Es sei
![A:=\{(x,y)\in[0,1]\times[0,1]: x\prec y\}](/pictures/dewiki/99/c0251a2b9bfdc2df570a8b00bd46cbcc.png) . Mit 1A bezeichnen wir die Indikatorfunktion der Menge A, also
. Mit 1A bezeichnen wir die Indikatorfunktion der Menge A, also ![1_A:[0,1]\times[0,1]\rightarrow\{0,1\}](/pictures/dewiki/101/e673d2cd8276256d30df2afc74b37c71.png) , mit 1A(x,y) = 1 genau dann, wenn
, mit 1A(x,y) = 1 genau dann, wenn 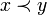 .
.Für jedes
![y\in [0,1]](/pictures/dewiki/97/ab3abad183cd9e117cb5711a60e1bc1d.png) sei
sei ![A_y :=\{x\in[0,1]: x\prec y\}](/pictures/dewiki/57/9d09cfa2c96da190e385360de33af71f.png) . Diese Menge ist für jedes y abzählbar, da T(y) als abzählbare Ordinalzahl nur abzählbar viele Vorgänger hat. Insbesondere ist daher Ay immer eine Lebesgue-Nullmenge: λ(Ay) = 0.
. Diese Menge ist für jedes y abzählbar, da T(y) als abzählbare Ordinalzahl nur abzählbar viele Vorgänger hat. Insbesondere ist daher Ay immer eine Lebesgue-Nullmenge: λ(Ay) = 0.Weiters definieren wir für jedes
![x\in [0,1]](/pictures/dewiki/99/c628ba2b1047de93f66cb815d986e107.png) die Menge
die Menge ![A^x :=\{y\in[0,1]: x\prec y\}](/pictures/dewiki/57/9031c25091b822181e335b5be83ce0ef.png) ; das Komplement jeder dieser Mengen ist abzählbar, somit gilt λ(Ax) = 1.
; das Komplement jeder dieser Mengen ist abzählbar, somit gilt λ(Ax) = 1.Dann gilt unter Verwendung des Lebesgue-Integrals und des Lebesgue-Maßes λ
aber
Die Funktion 1A ist also eine Funktion, die nach dem Satz von Tonelli nicht Lebesgue-messbar sein kann.
Einzelnachweise
- ↑ Vgl. J. Floyd, A. Kanamori: How Gödel Transformed Set Theory. in: Notices of the American Mathematical Society. Providence 53.2006, S.424. ISSN 0002-9920 (pdf, 103 KB)
Literatur
- Max Urchs: Klassische Logik - eine Einführung. Berlin 1993, S.112–121. ISBN 3-05-002228-0 (im Zusammenhang mit Kardinalzahlen)
- Kurt Gödel: The Consistency of the Axiom of Choice and of the Generalized Continuum Hypothesis with the Axioms of Set Theory. in: Annals of Mathematics Studies. Princeton University Press, Princeton NJ 3.1940. ISSN 0066-2313
- Kurt Gödel: What is Cantor's Continuum Problem? in: American Mathematical Monthly. Washington 54.1947, S.515–525, Errata 55.1947, S.151. ISSN 0002-9890
- Paul J. Cohen: Set Theory and the Continuum Hypothesis. Benjamin, New York 1966, Dover 2008. ISBN 0-486-46921-2
- Kenneth Kunen: Set Theory. North-Holland, Amsterdam 1980 (Kap. VI, Kap. VII §5f). ISBN 0-444-85401-0
Wikimedia Foundation.