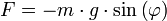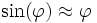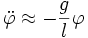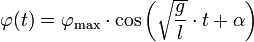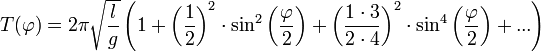- Fadenpendel
-
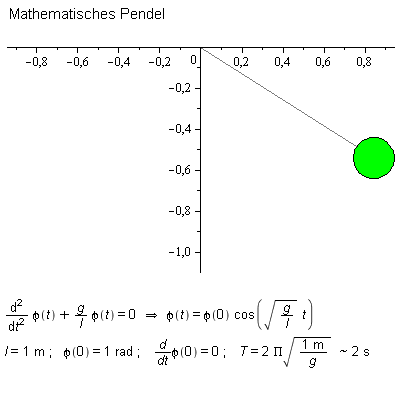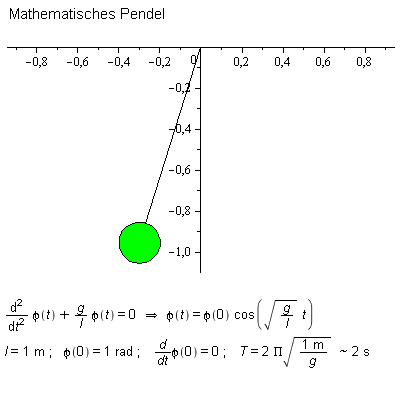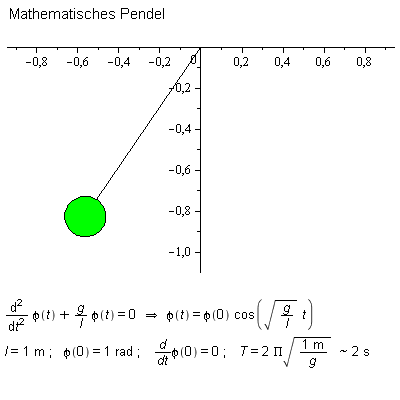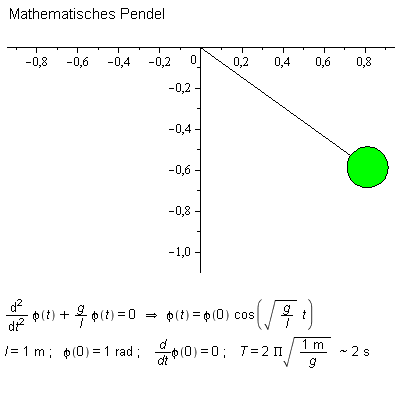
Ein mathematisches Pendel ist eine Idealisierung eines realen Pendels. Es ist ein grundlegendes Modell zum Verständnis von Pendelschwingungen.
Mathematische Pendel sind durch zwei wesentliche Eigenschaften charakterisiert:
- Es herrscht keine Reibung in irgendeiner Form, also weder Strömungswiderstand, noch innere Reibung in Faden und Aufhängepunkt
- Die gesamte Masse des Pendels ist in einem einzigen Punkt konzentriert. Der Faden wird als masselos betrachtet, die Massenverteilung des Pendelkörpers wird durch ihren Massenmittelpunkt dargestellt.
In der Praxis kann man ein mathematisches Pendel annähern, wenn der verwendete Faden möglichst lang und dünn, der Pendelkörper möglichst klein und schwer ist. Betrachtet man die Schwingungen in einer nicht allzu ausgedehnten Zeitspanne, kann man die Reibung meist ebenfalls vernachlässigen.
Eine typische Eigenschaft bei der Schwingung eines mathematischen Pendels ist, dass die Frequenz bei kleinen Auslenkungen nur von der Länge des Pendels abhängt, nicht aber von der anfänglichen Auslenkung oder der angehängten Masse.
Inhaltsverzeichnis
Mathematische Beschreibung
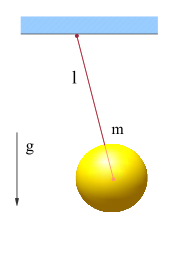
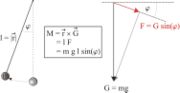
Die allgemeine Bewegungsgleichung zur Beschreibung eines solchen Pendels folgt aus dem Gesetz von Newton. Auf die Masse m wirkt die Schwerkraft FG = mg, wobei g die Fallbeschleunigung ist. Da der Faden eine Zwangskraft ausübt, die dafür sorgt, dass der Abstand der Masse zum Aufhängungspunkt konstant bleibt, wirkt effektiv nur die Komponente der Schwerkraft, die senkrecht zum Faden steht. Wenn
 der Auslenkungswinkel aus der Senkrechten ist, ist diese Komponente durch
der Auslenkungswinkel aus der Senkrechten ist, ist diese Komponente durchgegeben. Die Entfernung der Masse zum Ruhepunkt entlang des durch die Fadenlänge l gegebenen Kreises ist
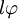 ; die Beschleunigung, also die zweite Ableitung nach der Zeit, ist
; die Beschleunigung, also die zweite Ableitung nach der Zeit, ist 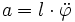 . Aus F = ma folgt
. Aus F = ma folgt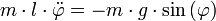 .
.
Es handelt sich um eine nichtlineare Differentialgleichung zweiter Ordnung.
Bei kleinen Auslenkwinkeln (
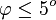 ) kann man die Kleinwinkelnäherung
) kann man die Kleinwinkelnäherung(
 im Bogenmaß) benutzen um zu linearisieren, so dass sich die Bewegungsgleichung zu
im Bogenmaß) benutzen um zu linearisieren, so dass sich die Bewegungsgleichung zuvereinfacht. Dies ist die Differentialgleichung der harmonischen Schwingung mit der allgemeinen Lösung
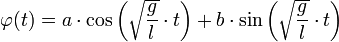 ,
,
was man äquivalent auch als
schreiben kann. Hierbei sind
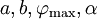 Konstanten, die von den Anfangsbedingungen abhängen. Die Lösung ist eine harmonische Schwingung mit der Periodendauer
Konstanten, die von den Anfangsbedingungen abhängen. Die Lösung ist eine harmonische Schwingung mit der Periodendauer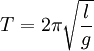 .
.
Abgesehen vom Proportionalitätsfaktor 2π lässt sich dieser Zusammenhang auch mit dem Buckinghamschen Π-Theorem herleiten. Die nur kosinusförmige Lösung ergibt sich, wenn man das Pendel am Anfang auslenkt und dann loslässt, ohne eine Kraft auszuüben. Die nur sinusförmige Lösung ergibt sich, wenn man dem ruhenden Pendel einen Schubs gibt.
Die Schwingungsfrequenz eines Pendels gibt man vorzugsweise als Kreisfrequenz an, da sich der Faktor 2π dann herauskürzt:
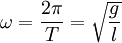 .
.
Reale Pendel
Da Pendel in der Realität immer mehr als infinitesimal ausgelenkt werden, verhalten sie sich nichtlinear. Die allgemeine Differentialgleichung ist elementar nicht lösbar und erfordert Kenntnisse über elliptische Integrale. Damit lässt sich die allgemeine Lösung in einer Reihe entwickeln:
Außerdem ist die Dämpfung durch Reibungsverluste bei einem echten Pendel größer als Null, so dass die Auslenkungen ungefähr exponentiell mit der Zeit abnehmen.
Siehe auch:
- physikalisches Pendel
- Foucaultsches Pendel
- Torsionspendel
- Gekoppelte Pendel
- Doppelpendel
- Multipendel
- Sekundenpendel
Weblinks
Wikimedia Foundation.

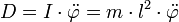
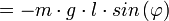 , wobei sich durch Division mit
, wobei sich durch Division mit