Kritische Blende

Abbildung 1: Die kritische Blende als Kompromiss aus Aberrationsunschärfe und Beugungsunschärfe

Abbildung 2: Das Auflösungsvermögen eines Makroobjektivs (y-Achse) in Abhängigkeit von der Blendenzahl (x-Achse)

Als kritische Blende bezeichnet man in der Fotografie die Blendeneinstellung, die das höchste Auflösungsvermögen bei der Aufnahme ermöglicht.

Definition

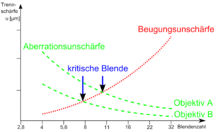
Theoretisch betrachtet hat ein Objektiv bei einer offenen Blende, das heißt bei der kleinsten möglichen Blendenzahl, das größte Auflösungsvermögen. Die Beugungsunschärfe ist hier am geringsten (in Abbildung 1 die rote Linie). Bei fast allen Objektiven sind allerdings die Abbildungsfehler (Aberrationen) bei offener Blende am größten (in Abbildung 1 die grünen Linien). Um diese Abbildungsfehler zu unterdrücken, schließt man die verursachenden Randstrahlen der Optik durch Abblenden aus. Mit zunehmendem Abblenden fällt das Auflösungsvermögen aber durch die ansteigende Beugungsunschärfe wieder ab. Die Kurve der Beugungsunschärfe ist bei einer Brennweite und Wellenlänge für alle Objektive gleich und kann nicht durch den Aufbau des Linsensystems beeinflusst werden. An dem Punkt, an dem sich die beiden Kurven im Diagramm schneiden, das heißt die Werte für beide Effekte halten sich die Waage, ist das höchste Auflösungsvermögen gewährleistet. Dieser Punkt wird als kritische Blende bezeichnet. Bei Zoomobjektiven kann die kritische Blende – je nach Brennweite – leicht unterschiedliche Werte annehmen.

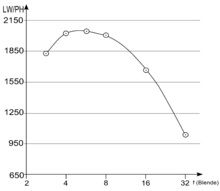
Bei den meisten Objektiven für das Kleinbildformat liegt die kritische Blende in der Regel bei mittleren Blendenwerten von 5,6 bis 8. In Abbildung 2 ist die kritische Blende aus Messwerten eines realen Makroobjektives grafisch als Maximum der Kurve bei einer Blendenzahl von 5,6 dargestellt.

In einigen Publikationen wird der Begriff der kritischen Blende mit dem der förderlichen Blende gleichgesetzt.^[1] Dies ist jedoch nicht korrekt. Bei der förderlichen Blende sind die Schärfentiefe und die Beugungsunschärfe die Gegenspieler, die durch eine entsprechende Blendenwahl zu einem Maximum an Auflösungsvermögen zu optimieren sind. Die gewünschte Schärfentiefe ist dabei jedoch vom abzubildenden Objekt, das heißt von dessen Ausdehnung in die räumliche Tiefe, und vom gewählten Abbildungsmaßstab abhängig.

Berechnung an plankonvexer Linse

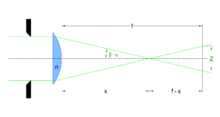
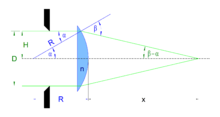Schnittweite x bei einer optischen Abbildung mit einer plankonvexen, sphärischen Linse mit der Brechzahl n = 1,5 und dem Krümmungsradius R bei gegebener Einfallshöhe H.

Anhand einer plankonvexen, sphärischen Linse kann die kritische Blende verhältnismäßig leicht veranschaulicht werden. Betrachtet man eine optische Abbildung aus dem Unendlichen mit parallelem, monochromatischem Licht der Wellenlänge λ durch eine solche Linse mit dem Krümmungsradius R und der Brennweite f ergibt sich die in nebenstehender Abbildung dargestellte Situation.

Durch Beugung ergibt sich in der Bildebene ein Beugungsscheibchen mit dem Durchmesser

$d = 2,44 \cdot \lambda \cdot \frac {f}{D} = 2,44 \cdot \lambda \cdot k$,

wobei D die Eintrittspupille der optischen Abbildung und

$k = \frac {f}{D}$

die Blendenzahl sind. Die Größe des Beugungsscheibchens ist also proportional zur Blendenzahl.

Zur Berechnung der sphärischen Aberration können Lichtstrahlen betrachtet werden, die im Abstand

$H = \frac {D}{2} = \frac {f}{2 \cdot k}$

parallel zur optischen Achse auf die gegenstandsseitige plane Linsenfläche fallen. Diese werden beim Eintritt in das optisch dichtere Medium des Linsenmaterials mit der Brechzahl n nicht gebrochen, da sie senkrecht auftreffen. Bildseitig bilden diese Strahlen zum Oberflächenlot der Linse in der Linse den Winkel α und außerhalb der Linse den Winkel β und werden entsprechend dem Snelliusschen Brechungsgesetz gebrochen. Dabei gilt:

$\sin(\alpha) = \frac {H}{R}$, also $\alpha = \arcsin\left(\frac {H}{R}\right) = \arcsin\left(\frac {f}{2 \cdot k \cdot R}\right)$

und

$\sin(\beta) = n \cdot \frac {H}{R}$, also $\beta = \arcsin\left(n \cdot \frac {H}{R}\right) = \arcsin\left(\frac {n \cdot f}{2 \cdot k \cdot R}\right)$

Die optische Achse schneiden diese Strahlen dann unter dem Winkel β − α. Die bildseitige Schnittweite x gemessen vom Scheitelpunkt der Linse ergibt sich dann in Abhängigkeit der Einfallshöhe H mit Hilfe des Sinussatzes zu:

$x(H) = {\frac {n \cdot H}{\sin(\beta-\alpha)}} - R$

Für achsennahe Strahlen vereinfacht sich diese Beziehung durch die Bildung des Grenzwertes mit H → 0 zu:

$x(0) = f = R \cdot \left(\frac {n}{n-1}-1\right)$,

wobei die Brennweite f und die Schnittweite x(0) der Linse dann identisch sind.

Unter Verwendung der Blendenzahl und der Brennweite ergibt sich die Schnittweite zu:

$x(H) = {\frac {n \cdot f}{2 \cdot k \cdot \sin(\beta-\alpha)}} - R$

Zerstreuungskreis mit dem Durchmesser Z bei einer optischen Abbildung mit einer plankonvexen, sphärischen Linse mit der der Brennweite f durch sphärische Aberration mit der Schnittweite x.

Durch die sphärische Aberration verschiebt sich der Schnittpunkt der Strahlen mit der optischen Achse umso näher an die Linse, je größer die Einfallshöhe H ist. In der Brennebene im Abstand f vom Scheitelpunkt der Linse ergibt sich daher keine punktförmige Abbildung mehr, sondern ein Zerstreuungskreis mit dem Durchmesser:

$Z = 2 \cdot (f - x) \cdot \tan(\beta-\alpha)$

Beispielrechnung

Bei einer Brechzahl n von 1,50 und einem Krümmungsradius R von 100 Millimetern ergibt sich also eine Brennweite f von 200 Millimetern.

Bei einer Wellenlänge λ im Grünen von 550 Nanometer ergibt sich der Durchmesser des Beugungsscheibchens zu

$d = 2,44 \cdot {550 nm} \cdot k = {1,342 \mu m} \cdot k$

Für verschiedene Blendenzahlen ergeben sich dann die in der folgenden Tabelle angegebenen Eintrittspupillen D und die Durchmesser d für das Beugungsscheibchen und Z für den Zerstreuungskreis (graphische Darstellung siehe rechts):

Kritische Blende am Schnittpunkt der beiden Kurven, die die Unschärfe durch das Beugungsscheibchen mit dem Durchmesser d (rot) und den Zerstreuungskreis durch den Öffnungsfehler mit dem Durchmesser Z (blau) logarithmisch über der Blendenzahl k darstellen.

Blendenzahl k	Eintrittspupille D in mm	Winkel α in °	Winkel β in °	Durchmesser Beugungsscheibchen d in µm	Durchmesser Zerstreuungskreis Z in µm
2,0	100,0	30,0	48,6	3	43553
2,8	70,7	20,7	32,0	4	11970
4,0	50,0	14,5	22,0	5	3835
5,7	35,4	10,2	15,4	8	1297
8,0	25,0	7,2	10,8	11	449
11,3	17,7	5,1	7,6	15	157
16,0	12,5	3,6	5,4	21	55
22,6	8,8	2,5	3,8	30	19
32,0	6,3	1,8	2,7	43	7

Die Blendenzahl der kritischen Blende liegt bei dieser optischen Abbildung zwischen 16,0 und 22,6, also ungefähr bei der Blendenzahl 20. Diese entspricht im angegebenen Beispiel einer Blendenöffnung D von 10 Millimetern. Die Durchmesser von Beugungsscheibchen und Zerstreuungskreis betragen in diesem Fall jeweils 27 Mikrometer.

Einzelnachweise

1. ↑ B. Ratfisch: Bernie's Fotolexikon, 2006

Literatur

• K. Kraus: Photogrammetrie, Band 1, Walter de Gruyter, 2004, S.68 ISBN 3-110-17708-0
• G. Olberg: Wissenschaftliche Tierphotographie, Deutscher Verlag der Wissenschaften, 1960

Weblinks

• schindler-mielke: kritische Blende