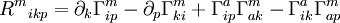Krümmungstensor

Der riemannsche Krümmungstensor (kürzer auch Riemanntensor oder Krümmungstensor) beschreibt die Krümmung von Räumen beliebiger Dimension, genauer gesagt differenzierbarer Mannigfaltigkeiten, auch wenn diese nicht mit einer riemannschen Metrik versehen sind, sondern mit einer Verallgemeinerung davon. Er wurde nach dem Mathematiker Bernhard Riemann benannt. Eine seiner wichtigsten Anwendungen findet er im Zusammenhang mit der Krümmung der Raumzeit in der allgemeinen Relativitätstheorie.

Der Riemanntensor ist eine vierfach indizierte Größe. Man kann ihn z. B. in der Form R^m_ikp angeben.

Definition

Zentrales Element differenzierbarer Mannigfaltigkeiten ist die kovariante Ableitung. Sie legt implizit fest, wie beliebige Größen, die an verschiedenen Punkten der Mannigfaltigkeit (4 - dimensionale Raumzeit im Falle der allgemeinen Relativitätstheorie) vorliegen, also etwa gemessen wurden, miteinander zu vergleichen sind. Sie umfasst in diesem Sinne eine Vorschrift, wie eine solche Größe von einem Punkt zum nächsten parallel zu transportieren ist.

Wird nun eine bestimmte Größe zwei hintereinander geschalteten beliebig kleinen Paralleltransporten in verschiedenen Richtungen unterworfen, also in Richtung eines Vektors 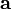$\mathbf a$ und anschließend in Richtung eines Vektors 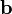$\mathbf b$, so kann diese Reihenfolge auch umgekehrt werden (zuerst 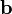$\mathbf b$, dann 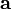$\mathbf a$), wenn es allein darum geht denselben Endpunkt der Verschiebung zu erreichen. Dennoch wird im Allgemeinen das Ergebnis der verschobenen Größe am Endpunkt verschieden sein, je nach dem, welchen der beiden Wege man gewählt hat. Die Abhängigkeit des Paralleltransportes vom Weg ist genau das Merkmal der Krümmung.

Der Krümmungstensor ist somit einfach durch die Differenz der zweiten kovarianten Ableitung entlang zweier aufeinanderfolgender Verschiebungsvektoren definiert.

Im Falle eines metrischen Raumes beinhaltet der Krümmungstensor die ersten und zweiten Ableitungen des metrischen Tensors, genauer gesagt besteht er aus den sogenannten Christoffelsymbolen und ihren Ableitungen:

$R^m{}_{ikp} = \partial_k \Gamma^m_{ip} - \partial_p \Gamma^m_{ki} + \Gamma^a_{ip} \Gamma^m_{ak} - \Gamma^a_{ik} \Gamma^m_{ap}$

Allgemeine Relativitätstheorie

Gezeitenkräfte

Zur Berechnung des Krümmungstensors bringt man das Gravitationsfeld in jedem Raumzeit-Punkt des gekrümmten Raumes zum Verschwinden und untersucht, wie die entstehenden flachen Räume der speziellen Relativitätstheorie miteinander zusammenhängen.

Dem Verschwinden des Gravitationsfeldes unter Koordinatentransformationen entspricht das Verschwinden des Gravitationsfeldes für einen Passagier in einem frei fallenden Aufzug. In einem inhomogenen Gravitationsfeld ist diese Transformation nur lokal möglich, d. h. für die unmittelbare Umgebung eines Raumzeit-Punktes.

Der Aufzug ist sehr klein gegen das Gravitationsfeld der Erde, die Inhomogenität des Feldes kann für die räumlichen Dimensionen des Aufzugs vernachlässigt werden, daher ist diese Transformation für Aufzüge in Gebäuden auf der Erdoberfläche möglich.

Analogon Kugeloberfläche

In Analogie betrachte man eine Kugel-Oberfläche. Diese gekrümmte Fläche hat in jedem Punkt eine Tangentialfläche. In der Nähe des Punktes unterscheiden sich die Tangentialfläche und die Umgebung des Punktes auf der Kugeloberfläche nur wenig.

Die Krümmung der Kugeloberfläche entspricht der Krümmung der Raumzeit, der Übergang zur Tangentialfläche entspricht dem Übergang zum flachen Raum.

Die Schwierigkeit bei der Kugeloberfläche besteht darin, den Zusammenhang zwischen den verschiedenen Tangentialflächen zu beschreiben. Je zwei Tangentialflächen haben eine unterschiedliche Orientierung im Raum.

Dieses Problem wird in der mathematischen Theorie der differenzierbaren Mannigfaltigkeiten gelöst.

Entsprechende Probleme hat man bei der gekrümmten Raumzeit. Zur Lösung verwendet man die kovarianten Ableitungen eines Vektorfeldes. Sind diese Ableitungen vertauschbar, so ist der Raum flach. Sind sie nicht vertauschbar, so ist er gekrümmt und die Krümmung kann durch den Riemanntensor beschrieben werden.

Abgeleitete Größen aus dem Krümmungstensor

Ricci-Tensor

In den Einsteinschen Feldgleichungen wird der so genannte Ricci-Tensor (nach Gregorio Ricci-Curbastro) R_μν verwendet. Er ergibt sich aus dem Krümmungstensor folgendermaßen:

$R_{\mu \nu} = \pm R^{\lambda}{}_{\mu \lambda \nu}$

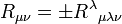
Über gleich vorkommende Indizes, von denen der eine oben und der andere unten stehen soll, wird summiert. Dies ist die so genannte Einsteinsche Summenkonvention. Zur Bildung des Ricci-Tensors wird über den Index λ summiert. Das Vorzeichen wird dabei per Konvention festgelegt und ist prinzipiell frei wählbar.

Die Bezeichnung der Indizes ist willkürlich, es ist egal ob man einen Index mit i,j oder m bezeichnet. Es kommt nur auf seine Position an.

Krümmungsskalar

Um den Krümmungsskalar (oder Ricci-Skalar, früher auch Laue-Skalar) herzuleiten, wird zunächst der Ausdruck R^λ_κ aus dem Ricci-Tensor hergeleitet:

R^λ_κ = g^μλR_μκ.

Der Krümmungsskalar ergibt sich folgendermaßen: R = R^λ_λ, d. h. es wird über den Index λ summiert. Dabei ist g^λκ der kontravariante metrische Tensor.

Weblinks

• Riemannscher Krümmungstensor auf MathWorld