Newtonsches Gravitationsgesetz

Das newtonsche Gravitationsgesetz wurde von Isaac Newton 1686 erstmals in seinem Werk Philosophiae Naturalis Principia Mathematica formuliert. Es besagt, dass jeder Massenpunkt jeden anderen Massenpunkt mit einer Kraft anzieht, die entlang der Verbindungslinie gerichtet ist. Der Betrag dieser Gravitationskraft ist proportional zum Produkt der beiden Massen und umgekehrt proportional zum Quadrat des Abstandes der beiden Massen.

Die newtonsche Gravitationstheorie liefert eine Erklärung für die drei 1609 und 1619 von Johannes Kepler veröffentlichten keplerschen Gesetze, und kann diese mit Hilfe der newtonschen Mechanik reproduzieren. Die Tatsache, dass die Theorie die keplerschen Gesetze ebenso wie die Erdgravitation erklärt, ist ein Beleg, dass sie in sehr guter Näherung die Gravitation beschreibt.

Mathematische Formulierung

Im newtonschen Gravitationsgesetz ist der Betrag der Kraft F zwischen zwei Massepunkten

$F = G\ \frac{m_1\, m_2}{r^2}$,

wobei m₁ und m₂ die jeweiligen Massen von Massepunkt 1 und 2 sind, und r der Abstand zwischen den Massepunkten ist. Die Gravitationskonstante G hat den Wert

$G = 6{,}674\,28(67) \, 10^{-11}\,\mathrm{\frac{m^3}{kg \, s^2}}$

Die auf die beiden Körper wirkende Kraft wirkt immer in Richtung des jeweils anderen Massepunkts; das newtonsche Gravitationsgesetz beschreibt damit im Gegensatz zum mathematisch ähnlichen coulombschen Gesetz immer eine anziehende Kraft. In vektorieller Form ist die auf Massepunkt 1 wirkende Kraft $\vec F$ gegeben durch

$\vec{F} = G \, m_1 \, m_2 \frac{\vec{x}_2-\vec{x}_1}{|\vec{x}_2-\vec{x}_1|^3}$,

wobei $\vec x_1$ und $\vec x_2$ die jeweiligen Positionen der beiden Teilchen sind. Die Betragsstriche im Nenner des Ausdrucks stehen für den Betrag des Vektors. Wird der Massepunkt 1 von mehreren Massepunkten 2, 3, ... gravitativ beeinflusst, so addieren sich die einzelnen Kräfte zur auf Massepunkt 1 wirkenden Gesamtkraft

$\vec{F} = G \, m_1 \, m_2 \frac{\vec{x}_2-\vec{x}_1}{|\vec{x}_2-\vec{x}_1|^3} + G \, m_1 \, m_3 \frac{\vec{x}_3-\vec{x}_1}{|\vec{x}_3-\vec{x}_1|^3} + \dots$.

Eigenschaften

Gravitationsbeschleunigung

Gravitation der Erde aus großer Entfernung

Gravitation in einem Raum auf der Erdoberfläche: Die Erdkrümmung kann auf dieser Größenskala vernachlässigt und die Kraftrichtungen überall parallel angenommen werden.

Die Beschleunigung, die eine Masse durch Gravitation erfährt, ist die Gravitationsbeschleunigung. Für diese Beträge der Beschleunigungen a₁ und a₂, die zwei Punktmassen m₁ und m₂ im Abstand r bei Abwesenheit anderer Kräfte erfahren, ergibt sich nach dem zweiten newtonschen Axiom:

$a_1 = \frac{F}{m_1} = G\, \frac{m_2}{r^2} \, ,$

und

$a_2 = \frac{F}{m_2} = G\, \frac{m_1}{r^2} \, .$

Die Punktmasse m₁ zieht die Masse m₂ an und umgekehrt. Die beiden Einzelbeschleunigungen beziehen sich dabei auf den gemeinsamen Schwerpunkt. Die Gesamtbeschleunigung der Körper aufeinander zu ist die Summe der Einzelbeschleunigungen, und ihr Betrag ist

$a_1 + a_2 = G\, \frac{m_1+m_2}{r^2}$

Falls nun eine der Massen viel kleiner ist als die andere, reicht es, die größere Masse zu berücksichtigen. So ist die Erde viel schwerer als ein Apfel, ein Mensch oder ein LKW, so dass es für alle diese Objekte reicht, die Masse der Erde in die Gleichung für die Beschleunigung einzusetzen. Alle drei Objekte werden, wenn sie sich an dem selben Ort befinden, gleich stark in Richtung Erdmitte beschleunigt. Sie fallen gleich schnell und in dieselbe Richtung. Wenn man jedoch ein Doppelsternsystem betrachtet, muss man beide Sternenmassen berücksichtigen, weil sie etwa gleich groß sind.

Wenn sich r während der Bewegung eines Objektes nur sehr geringfügig verändert, ist die Gravitationsbeschleunigung praktisch konstant, etwa bei einem Gegenstand nahe der Erdoberfläche, der nur einige Meter tief fällt, also verschwindend wenig im Vergleich zum Erdradius von r = ca. 6370 km. Bei einem sehr langen Objekt dagegen, z. B. einem hochkant ausgerichteten Stab der Länge r/2, wäre die Gravitationsbeschleunigung am unteren Ende des Stabes sehr viel größer als am oberen, mit der Folge, dass die Gravitationskräfte versuchen würden, den Stab auseinander zu ziehen. Spektakulärstes Beispiel solcher „Gezeitenkräfte“ ist die von Stephen Hawking in seinem Buch Die illustrierte kurze Geschichte der Zeit erwähnte Tatsache, dass ein in ein schwarzes Loch stürzender Astronaut dabei von diesen Kräften zerrissen würde ^[1].

Gravitationsfeld

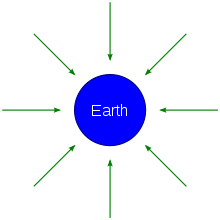
Das Gravitationsfeld ist ein Vektorfeld, das für alle Punkte im Raum die an der jeweiligen Stelle auf ein Objekt wirkende Gravitationsfeldstärke angibt. Das Gravitationsfeld einer im Koordinatenursprung (0|0|0) ruhenden Punktmasse M kann dabei, wie schon weiter oben erläutert, durch folgende Gleichung beschrieben werden, in der der Feldvektor $\vec{g}(\vec{r})$ stets zu der Masse M hinzeigt:

$\vec{g}(\vec{r}) = - G\,M \frac{\vec r}{r^3}$,

Im Fall mehrerer Punktmassen m_i dagegen kompliziert sich die Situation, und das Gesamtfeld ergibt sich nun als vektorielle Summe der einzelnen Felder gemäß folgender Gleichung:

$\vec{g}(\vec{r}) = -G \sum_{i} {m_i}\, \frac{\vec{r} - \vec{x_i}}{|\vec{r}-\vec{x_i}|^3}$

Ausgedehnte Körper

Reale Körper sind keine Punktmassen, sondern haben eine räumliche Ausdehnung. Da das Gravitationsgesetz linear in den Massen ist, kann man den Körper gedanklich in kleine Teile zerlegen und ihre Beiträge wie im vorigen Abschnitt gezeigt (vektoriell) addieren. Vollzieht man schließlich den Grenzübergang zu unendlich kleinen Teilen, ergibt sich statt einer herkömmlichen Summe ein Integral.

Auf diese Weise kann u.a. gezeigt werden, dass ein Objekt mit sphärisch symmetrischer Massenverteilung sich von außen betrachtet genauso verhält wie eine Punktmasse im Schwerpunkt des Körpers. Newton hat dieses Theorem in Philosophiae Naturalis Principia Mathematica bewiesen. Für nicht sphärisch symmetrische Körper dagegen gilt es im allgemeinen nicht.

Grenzen der Theorie

Obwohl es für praktische Zwecke hinreichend genau ist, ist das newtonsche Gravitationsgesetz nur eine Näherung für schwache und zeitunabhängige Gravitationsfelder. Für starke Felder verwendet man die genauere Beschreibung mittels der allgemeinen Relativitätstheorie, aus welcher die Poisson-Gleichung der klassischen Gravitationstheorie und damit auch das newtonsche Gravitationsgesetz direkt hergeleitet werden kann, wenn man nur annimmt, dass es sich bei der Gravitation um ein konservatives Feld handelt. Man bezeichnet das Gesetz daher heute oft als Grenzfall kleiner Felder. Die allgemeine Relativitätstheorie löst insbesondere auch die hier beschriebenen Probleme der newtonschen Gravitationstheorie.

Theoretische Grenzen

• Die newtonsche Theorie ist eine effektive Theorie, das bedeutet, sie gibt weder eine Ursache für die Gravitationskraft an, noch erklärt sie, wie das Feld über die Entfernung wirken kann. Diese geisterhafte Fernwirkung war auch für Newton unbefriedigend. Um diese Erklärungslücke zu schließen, wurde die sogenannte Le-Sage-Gravitation als Modell entwickelt, das sich jedoch nie wirklich durchsetzen konnte.
• Die newtonsche Theorie setzt voraus, dass sich die Gravitationswirkung unendlich schnell ausbreitet, damit die keplerschen Gesetze erfüllt sind. Dies führte sehr viel später zu Konflikten mit der speziellen Relativitätstheorie. Diese fordert nämlich, dass sich auch die Gravitation nur mit Lichtgeschwindigkeit ausbreitet.
• Die Äquivalenz von träger und schwerer Masse ist in der newtonschen Mechanik nicht erklärt.

Widersprüche zur Beobachtung

• Die newtonsche Theorie erklärt nicht vollständig die Periheldrehung der Planetenumlaufbahnen, besonders des Merkur. Bei diesem beträgt der Unterschied zwischen der nach der newtonschen Theorie berechneten und der beobachteten Periheldrehung 43 Bogensekunden pro Jahrhundert.
• Ob Licht im Gravitationsfeld abgelenkt wird oder nicht, hängt in der newtonschen Theorie davon ab, welche Natur dem Licht zugeschrieben wird. Wird es als elektromagnetische Welle aufgefasst, dann ergibt sich keine Ablenkung. Wird es jedoch gemäß der Korpuskeltheorie als massebehaftetes Teilchen aufgefasst, dann ergibt sich gemäß dem newtonschen Gravitationsgesetz eine Lichtablenkung, wobei aus der Bewegungsgleichung eine Vorhersage gemacht werden kann, die unabhängig von der Masse ist und somit auch im Grenzfall verschwindender Masse gültig bleibt. Dieser Wert beträgt jedoch nur die Hälfte der tatsächlich beobachteten Ablenkung, welche ausschließlich mit der allgemeinen Relativitätstheorie erklärt werden kann.

Einzelnachweise

1. ↑ Stephen Hawking: Die illustrierte kurze Geschichte der Zeit, Rowohlt-Verlag 2004, S.113-114.