- Lemma von Schwarz
-
Das schwarzsche Lemma (nach Hermann Schwarz) ist eine Aussage der Funktionentheorie über holomorphe Endomorphismen der Einheitskreisscheibe, welche einen Fixpunkt aufweisen.
Inhaltsverzeichnis
Aussage
Es bezeichne
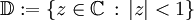 die Einheitskreisscheibe. Sei
die Einheitskreisscheibe. Sei 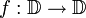 eine holomorphe Funktion mit f(0) = 0. Dann gilt
eine holomorphe Funktion mit f(0) = 0. Dann gilt 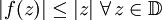 und
und 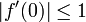 . Falls in einem Punkt
. Falls in einem Punkt 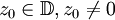 die Gleichheit | f(z0) | = | z0 | besteht oder | f'(0) | = 1 gilt, so ist
die Gleichheit | f(z0) | = | z0 | besteht oder | f'(0) | = 1 gilt, so ist 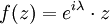 für ein passendes
für ein passendes 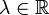 .
.Beweisidee
Man definiert die Funktion g(z): = f(z) / z. Wegen f(0) = 0 lässt sich g im Nullpunkt holomorph fortsetzen mit Wert g(0) = f'(0). Die Aussagen des Lemmas folgen dann durch Anwendung des Maximumprinzips auf g.
Anwendungen
- Bestimmung der holomorphen Automorphismengruppe der Einheitskreisscheibe:
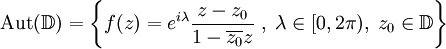 .
.
- Hieraus kann man die Automorphismengruppe der oberen Halbebene
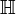 bestimmen und erhält
bestimmen und erhält 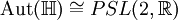 .
.
- Das schwarzsche Lemma ist eines der Hilfsmittel, die beim modernen, mit Hilfe normaler Familien geführten Beweis des riemannschen Abbildungssatzes verwendet werden.
- Lemma von Schwarz-Pick: Für holomorphe Funktionen
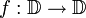 gilt
gilt 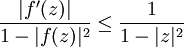 für alle
für alle 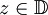 .
.
Verschärfung
Das schwarzsche Lemma besagt unter anderem, dass für eine holomorphe Funktion
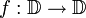 mit f(0) = 0 in der Potenzreihenentwicklung
mit f(0) = 0 in der Potenzreihenentwicklung 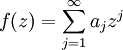 die Bedingung
die Bedingung 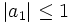 gilt. Ludwig Bieberbach zeigte, dass für injektive Funktionen auch
gilt. Ludwig Bieberbach zeigte, dass für injektive Funktionen auch 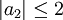 gilt, und stellte die später nach ihm benannte bieberbachsche Vermutung auf, dass
gilt, und stellte die später nach ihm benannte bieberbachsche Vermutung auf, dass 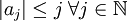 . Diese Vermutung wurde 1985 von Louis de Branges de Bourcia bewiesen.
. Diese Vermutung wurde 1985 von Louis de Branges de Bourcia bewiesen.Literatur
- Wolfgang Fischer, Ingo Lieb: Funktionentheorie. Vieweg Verlag, Braunschweig 2003, ISBN 3-528-77247-6
- Bestimmung der holomorphen Automorphismengruppe der Einheitskreisscheibe:
Wikimedia Foundation.
