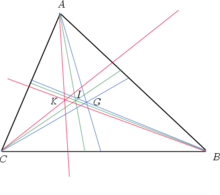
Lemoinepunkt

Lemoine-Punkt als Schnittpunkt der Symmedianen (rot)

Der Lemoinepunkt eines Dreiecks, auch Lemoinescher Punkt, Grebepunkt oder Symmedianenpunkt genannt, ist ein ausgezeichneter Punkt im Dreieck und zwar der Schnittpunkt von dessen Symmedianen.

Eigenschaften

• Der Lemoinepunkt ist definitionsgemäß isogonal konjugiert zum Schwerpunkt.

• Wenn wir das Dreieck mit ABC bezeichnen und den Lemoinepunkt mit L, dann sind die Abstände des Punktes L zu den Geraden BC, CA und AB proportional zu den Längen der Seiten BC, CA und AB des Dreiecks ABC.

• Der Lemoinepunkt ist Lösung eines gelegentlich wichtigen Optimierungsproblems: Wenn wir einen Punkt P in der Ebene des Dreiecks ABC betrachten, dann ist die Summe der Quadrate der Abstände von dem Punkt P zu den Seiten BC, CA und AB genau dann minimal, wenn P mit dem Lemoinepunkt L des Dreiecks ABC übereinstimmt.

• Der Lemoinepunkt des größeren Dreiecks, das durch die drei Ankreismittelpunkte bestimmt wird, ist der sogenannte Mittenpunkt des Dreiecks.

Koordinaten

Lemoine-Punkt (Symmedianenpunkt, Grebe-Punkt, X6)
Trilineare Koordinaten	$a \, : \, b \, : \, c = \, \sin\alpha \, : \, \sin\beta \, : \, \sin\gamma$
Baryzentrische Koordinaten	$a^2 \, : \, b^2 \, : \, c^2$

Weblinks

• Eric W. Weisstein: Symmedian Point. In: MathWorld. (englisch)
• X6 Der Symmedian Point Eine umfangreiche Darstellung mit diversen weiterführenden Aussagen