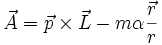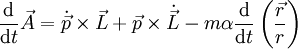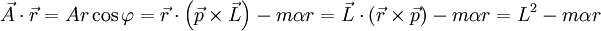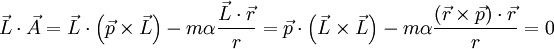- Lenzscher Vektor
-
Der Laplace-Runge-Lenz-Vektor (in der Literatur auch Runge-Lenz-Vektor, Lenz-Runge-Vektor etc., nach Pierre-Simon Laplace, Carl Runge und Heinrich Friedrich Emil Lenz) ist eine Erhaltungsgröße der Bewegung im V(r) = − α / r-Potenzial (Coulomb-Potenzial, Gravitationspotenzial).
Er ist definiert als
mit
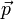 : Impuls des Körpers
: Impuls des Körpers : Drehimpuls des Körpers
: Drehimpuls des Körpers- m: Masse des Körpers
- α: Proportionalitätskonstante des Potenzials, γmM für Kepler, q1q2 / (4πε0εr) für Coulomb
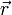 : Ortsvektor des Körpers
: Ortsvektor des Körpers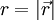 : Betrag des Ortsvektors
: Betrag des Ortsvektors
und ermöglicht die elegante Herleitung der Bahnkurve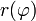 eines Teilchens (z.B. Planet im Keplerproblem, Elektron im Wasserstoffatom), worauf die resultierende Kraft eines solchen Potenzials wirkt.
eines Teilchens (z.B. Planet im Keplerproblem, Elektron im Wasserstoffatom), worauf die resultierende Kraft eines solchen Potenzials wirkt.Inhaltsverzeichnis
Beweis der Erhaltung
Die totale Zeitableitung des Runge-Lenz-Vektors muss verschwinden. Man erhält:
In diesem System haben wir Isotropie. Daher gilt die Drehimpulserhaltung (
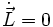 ).
).Das Potential V erzeugt eine (konservative) Kraft nach
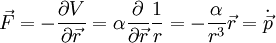 .
.
Der Drehimpuls ist definiert als
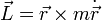 . Somit erhält man:
. Somit erhält man:Wegen
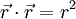 gilt:
gilt: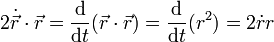 , also:
, also: 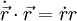 .
.
Damit gilt schließlich
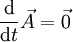 , mit anderen Worten die Konstanz des Runge-Lenz-Vektors.
, mit anderen Worten die Konstanz des Runge-Lenz-Vektors.Herleitung der Bahnkurve
Hierfür ist normalerweise eine aufwändige Integration mit mehreren Substitutionen nötig, aus der Multiplikation des Runge-Lenz-Vektors mit
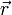 folgt nun aber einfach nach der Kosinusbeziehung des Skalarprodukts (pfeillose Buchstaben kennzeichnen stets die Beträge des zugehörigen Vektors):
folgt nun aber einfach nach der Kosinusbeziehung des Skalarprodukts (pfeillose Buchstaben kennzeichnen stets die Beträge des zugehörigen Vektors):Hierbei wurde die Zyklizität des Spatproduktes sowie die Drehimpulsdefinition genutzt.
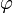 bezeichnet den Winkel zwischen Runge-Lenz- und Ortsvektor.
bezeichnet den Winkel zwischen Runge-Lenz- und Ortsvektor.Man kann das noch ein wenig umschreiben und erhält dadurch die typische Kegelschnittgleichung in Polarkoordinaten:
Dabei ist ε = A / mα die numerische Exzentrizität des Kegelschnitts, die die Bahnform Kreis (ε = 0), Ellipse (0 < ε < 1), Parabel (ε = 1) oder Hyperbel (ε > 1) bestimmt.
Eigenschaften
- Der Runge-Lenz-Vektor liegt in der Bahnebene, denn er steht senkrecht zum Drehimpulsvektor:
- Der Runge-Lenz-Vektor zeigt zum Perihel, d.h. zentrumnächsten Punkt der Bahn. Dies folgt sofort aus obiger Bahngleichung, da
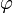 den Winkel zwischen Orts- und Runge-Lenz-Vektor darstellt und r minimal ist für maximalen Nenner, d.h.
den Winkel zwischen Orts- und Runge-Lenz-Vektor darstellt und r minimal ist für maximalen Nenner, d.h. 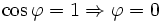 .
.
- Der Runge-Lenz-Vektor hat als Betrag das mα-fache der numerischen Exzentrizität der Bahnkurve. Dies wurde bereits bei der Herleitung derselben gezeigt.
Bedeutung: keine Periheldrehung im Keplerpotenzial
Die Erhaltung des Runge-Lenz-Vektors impliziert, als unmittelbare Folge des Gesagten, dass sich die Ellipsen der Planetenbewegung im Kepler-Potenzial (-a/r-Potenzial) nicht drehen (keine sog. Periheldrehung, wie sie generell bei Abweichungen von diesem Potenzial, z. B. aufgrund der anderen Planeten oder infolge der Einstein'schen Relativitätstheorien, auftreten würde).
Auch in der Quantenmechanik ergeben sich in einem Potenzial der obigen Art Besonderheiten (siehe Wasserstoffatom).
Wikimedia Foundation.