Lindeverfahren

Das Linde-Verfahren ist eine 1895 von Carl von Linde entwickelte technische Methode, welche die Verflüssigung von atmosphärischen Gasen und Gasgemischen wie Luft, Sauerstoff, Stickstoff und Argon in großen Mengen ermöglicht und in diesem Sinne der Kälteerzeugung im Temperaturbereich von 77 bis 100 Kelvin (K) dient. Zuerst wurde das Verfahren nur für akademische Zwecke verwendet. Recht schnell - 1902 - kam es zu einer echten industriellen Anwendung, nachdem die erste Luftzerlegungsanlage ebenfalls unter Leitung von Carl von Linde entwickelt und gebaut wurde: das Linde-Verfahren wurde in die Linde'sche Luftzerlegungsanlage integriert und diente hauptsächlich der Kälteerzeugung, aber auch der Verflüssigung von Produkten, falls es notwendig war. Später wurden ergiebigere Kälteerzeugungsverfahren (mit Entspannung in einem Hubkolbenexpander oder einer Entspannungsturbine) entwickelt, so dass das klassische Linde-Verfahren an Bedeutung verlor und seitdem kaum noch Verwendung findet.

Diese weitere Erfindung von Carl von Linde - die Luftzerlegungsanlage - hat jedoch mit der Zeit an der Bedeutung nur gewonnen. Heute werden großtechnisch bedeutsame Mengen an gasförmigem und flüssigem Sauerstoff (GOX und LOX), Stickstoff (GAN und LIN) und Edelgasen mit Hilfe von Luftzerlegungsanlagen (technische Abkürzung: LZA) hergestellt.

Prinzip

Das Linde-Fränkl-Verfahren

Das Entspannen eines realen Gases wird von einer Änderung seiner Temperatur begleitet, das abstrakte Modell des idealen Gases zeigt diesen Effekt nicht. Ob die Temperaturänderung in Form von Abkühlung oder Erwärmung auftritt, hängt davon ab, ob die Inversionstemperatur (also die Temperatur, bei welcher der Joule-Thomson-Koeffizient des Gases einen Vorzeichenwechsel erfährt) überschritten ist. Befindet sich das System über der Inversionstemperatur, so erwärmt sich das Gas bei Expansion (genauer: isenthalper Expansion, die Enthalpie ändert sich durch die Volumenänderung nicht), geringere Temperaturen haben eine Abkühlung zur Folge; dieser Effekt wird im Linde-Verfahren genutzt. Siehe auch Joule-Thomson-Effekt.

Um die für viele Gase niedrige Siedetemperatur zu erreichen (für Sauerstoff −183 °C, für Stickstoff −196 °C), benutzt man das entspannte Gas im Gegenstromprinzip zur Vorkühlung des verdichteten Gases.

Anwendung

Vereinfachung des Linde-Verfahrens

Das Linde-Verfahren wurde früher zur Abkühlung von atmosphärischen Gasen Sauerstoff, Stickstoff sowie Argon und andere Edelgase bis zur Verflüssigung benutzt.

Luftverflüssigung

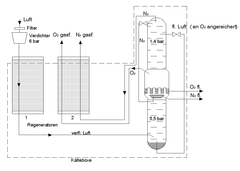
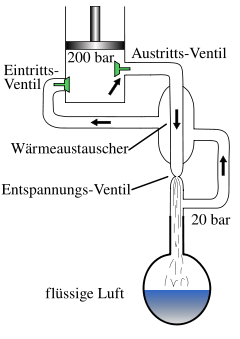
Die Luft wird zunächst von Wasserdampf, Staub und Kohlendioxid befreit. Ein Kompressor verdichtet die Luft dann auf einen Druck von 200 bar. Dabei erhöht sich ihre Temperatur um ca. 45 Kelvin, also beispielsweise von +20°C auf ca. +65°C. In einem ersten Wärmeüberträger wird die verdichtete, erhitzte Luft dann vorgekühlt und die Temperatur wieder in den Bereich der Umgebungstemperatur zurückgeführt. Dabei wird Wärme aus dem Luftverflüssigungssystem in die Umgebung abgegeben. Anschließend wird die Luft über ein Expansionsventil oder eine Turbine entspannt, wobei ihre Temperatur im ersten Schritt um ca. 45 Kelvin auf ca. −25 °C sinkt. Diese abgekühlte Luft wird über einen Gegenstrom-Wärmeübertrager in den Kompressor zurückgeleitet und dient somit zur Kühlung weiterer komprimierter Luft vor deren Entspannung. Durch diesen Prozess wird die Luft allmählich so tief gekühlt, dass bei 20 bar die Verflüssigung eintritt.

Dem oberbayerischen Ingenieur Fränkl gelang es, die Gegenstromrekuperatoren durch Regeneratoren zu ersetzen. Diese lassen sich weitaus kleiner, preiswerter und leistungsfähiger bauen als Gegenstromrohrbündeltauscher. Diese Erfindung wurde vom Unternehmen Linde AG übernommen und unter dem Namen Linde-Fränkl-Verfahren vermarktet. Das Verfahren mit Regeneratoren wurde erfolgreich (bis ca. 1970) angewandt, bis eine neuere Technologie (wieder rekuperative Gegenstrom-Plattenwärmetauscher mit vorgeschalteter adsorptiver Trocknung und Reinigung) aufkam.

In einem offenen Gefäß unter Atmosphärendruck nimmt flüssige Luft eine Temperatur von etwa −190 °C = 83 K an. Dabei siedet sie, so dass ihre niedrige Temperatur erhalten bleibt, denn dadurch wird der flüssigen Luft Verdampfungswärme entzogen. Die Menge der absiedenden Luft regelt sich so ein, dass die durch Wärmeleitung oder Einstrahlung zugeführte Wärme gleich der verbrauchten Verdampfungswärme ist. Je nach Größe und Isolierung des Behälters kann so die flüssige Luft einige Stunden bis viele Tage erhalten bleiben. Flüssige Luft darf jedoch keinesfalls in verschlossenen Behältern ohne Sicherheitseinrichtungen und entsprechender Auslegung aufbewahrt werden, da der durch allmähliche Erwärmung steigende Innendruck diese sonst zum Bersten bringt.

Fraktionieren der verflüssigten Luft

Siedender Stickstoff in einem Metallbecher(-196°C)

Flüssige Luft kann mittels Fraktionieren in ihre Bestandteile zerlegt werden: Man nutzt die unterschiedlichen Siedepunkte der einzelnen Luftbestandteile aus. Allerdings liegen die Siedepunkte von Sauerstoff und Stickstoff sehr dicht zusammen. Man benutzt daher eine Rektifikationssäule: Die flüssige Luft läuft über mehrere Rektifikationsböden im Gegenstrom zum aufsteigenden Gas nach unten. Sie nimmt den Sauerstoff aus dem Gas auf und gibt Stickstoff ab.

Dadurch wird die Flüssigkeit sauerstoffhaltiger, das Gas stickstoffhaltiger.

Verflüssigung von Wasserstoff und Helium

Um das Linde-Verfahren zur Wasserstoff und Helium-Verflüssigung anwenden zu können, muss man diese Gase erst unter die Inversionstemperatur (siehe unter Physikalische Grundlagen und Joule-Thomson-Effekt) T_i vorkühlen. Dies geschieht in der Regel mit flüssiger Luft.

Das schließlich erhaltene flüssige Helium siedet unter Atmosphärendruck bei 4,2 K. Dies ist der niedrigste Siedepunkt aller Elemente. Durch Abpumpen des Helium-Gases über dem siedenden Helium wird letzterem Verdampfungswärme entzogen, so dass sich seine Temperatur weiter senken lässt. Da der Dampfdruck mit der Temperatur aber sehr stark abfällt, erreicht man mit diesem Verfahren keine tiefere Temperatur als 0,84 K; zu ihr gehört der Dampfdruck 0,033 mbar.

Physikalische Grundlagen

Das Linde-Verfahren beruht auf dem Joule-Thomson-Effekt: Im idealen Gas üben die Teilchen keine Wechselwirkung aufeinander aus, weshalb die Temperatur des idealen Gases nicht vom Volumen abhängt. Reale Gase sind jedoch nicht ideal: Es gibt Wechselwirkungen, die sich mit Konstanten a und b ausdrücken, falls man das Gas mit Hilfe der Van-der-Waals-Gleichung beschreibt.

Der Energiegehalt des realen Gases ändert sich also auch bei adiabatischer (ohne Wärmeaustausch) Entspannung, ohne dass äußere Arbeit verrichtet wurde. Das ist durch die Temperaturänderung nachweisbar.

Verbindet man zwei Gasbehälter mit einer porösen Wand und drückt das im Raum 1 unter Druck stehende Gas mit einem Kolben langsam durch diese Membran, die zur Verhinderung von Wirbeln und Strahlbildung dient, in Raum 2, der unter einem konstanten, aber geringeren Druck als Raum 1 steht, dann stellt sich ein kleiner Temperaturunterschied zwischen den beiden Räumen ein. Er beträgt bei Kohlenstoffdioxid etwa 0,75 K pro bar Druckdifferenz, bei Luft etwa 0,25 K.

Erklärbar ist das, wenn man bedenkt, dass im Raum 1 das Volumen V₁ entfernt wurde. Der Kolben hat dem Gas die Arbeit p₁V₁ zugeführt. Die Gasmenge taucht im Raum 2 auf und muss die Arbeit p₂V₂ gegen den Kolben leisten. Die Differenz der Arbeit ist als innere Energie dem Gas zugute gekommen.

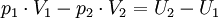$p_1 \cdot V_1 - p_2 \cdot V_2 = U_2 - U_1$ bzw. $U_1 + p_1 \cdot V_1 = U_2 + p_2 \cdot V_2$

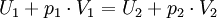
Die Enthalpie 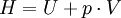$H = U + p \cdot V$ bleibt konstant. Dazu kommt beim van der Waals-Gas noch die kinetische Energie 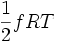$\frac{1}{2} f R T$ und die potentielle Energie 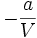$-\frac{a}{V}$, die sich als Arbeit gegen die Kohäsionskräfte der Teilchen ergibt. Sie steht in enger Verbindung mit dem Binnendruck 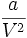$a \over V^2$ und ergibt sich aus einer Volumenintegration.

Damit ergibt sich unter der Berücksichtigung der van-der-Waals-Gleichung:

$H = U + p V =\frac{1}{2}fRT-\frac {a}{V} + \left( \frac{RT}{V-b}-\frac{a}{V^2}\right)\cdot V=RT\left(\frac{f}{2}+\frac{V}{V-b} \right)-\frac{2a}{V}$

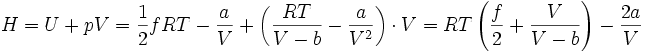
Weil die Enthalpie erhalten bleibt, gilt daher für das totale Differential: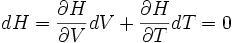

$dH = \frac{\partial H}{\partial V}dV + \frac{\partial H}{\partial T}dT = 0$

Umgeformt nach der Änderung der Temperatur dT ergibt sich:

$dT=- \frac{\dfrac{\partial H}{\partial V}dV}{\dfrac{\partial H}{\partial T}} = \frac{ \dfrac{bT}{(V-b)^2}-\dfrac{2a}{RV^2}}{\dfrac{f}{2} + \dfrac{V}{V-b}} dV \approx \frac{bRT - 2a}{\left(\dfrac{1}{2}f +1 \right)RV^2} dV$

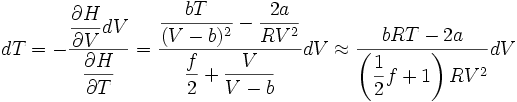
Der Zähler ist bei hoher Temperatur positiv. Er wechselt sein Vorzeichen bei der Inversionstemperatur $T_i = {2a \over Rb}$.

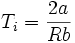Die kritische Temperatur für ein van der Waals Gas ist 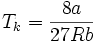$T_k = {8a \over {27 R b}}$ also $T_i = 6{,}75\,T_k$.

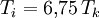Oberhalb von T_i erwärmt sich ein Gas bei Entspannung, unterhalb kühlt es sich ab. Für Kohlenstoffdioxid und Luft liegt T_i deutlich über der Zimmertemperatur, für Wasserstoff dagegen bei −80 °C.

Ein hoher Wert der van der Waals-Konstanten a bewirkt daher, dass die Temperatur bei Entspannung des realen Gases stark absinkt. Das ist logisch, denn bei Volumenvergrößerung entfernen sich die Moleküle voneinander und müssen dabei Arbeit gegen die durch a charakterisierten Anziehungskräfte verrichten. Diese Arbeit vermindert die kinetische Energie der Moleküle und damit die Temperatur des Gases.

Literatur

• Christian Gerthsen, Kneser, Vogel: Physik: ein Lehrbuch zum Gebrauch neben Vorlesungen. 14. Auflage. Springer Verlag, Berlin, Heidelberg, 1982. ISBN 3-540-11369-X (782 S.). Kapitel 5.6.6 und 5.6.7.
• Georg Veranneman: Technische Gase. Herstellung, Verteilung, Anwendung. 4., neu bearb. u. erw. Aufl. Verlag Moderne Industrie, o.O., 1988. ISBN 3-478-93229-7 (broschiert, 70 Seiten).

Weblinks

• Flash-Animation auf der Seite der Linde AG: http://www.linde-gase.de/produkte/industriegase/produktion_verfluessigung.html